Seoung Kyou Lee
Local Policies for Efficiently Patrolling a Triangulated Region by a Robot Swarm
Oct 08, 2014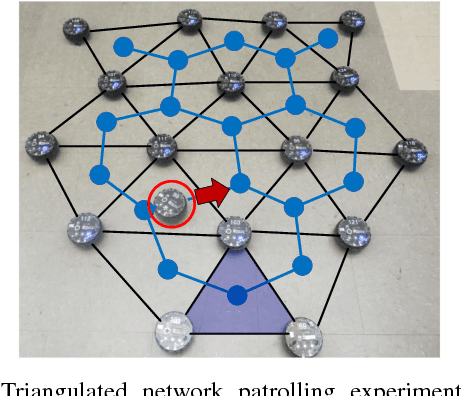
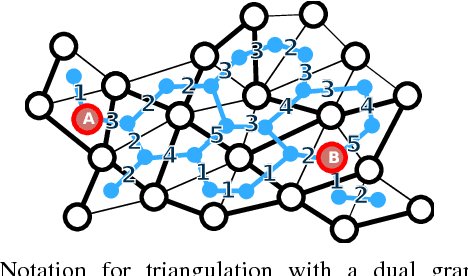
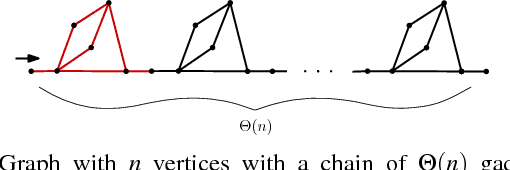
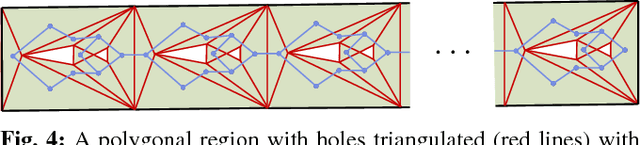
Abstract:We present and analyze methods for patrolling an environment with a distributed swarm of robots. Our approach uses a physical data structure - a distributed triangulation of the workspace. A large number of stationary "mapping" robots cover and triangulate the environment and a smaller number of mobile "patrolling" robots move amongst them. The focus of this work is to develop, analyze, implement and compare local patrolling policies. We desire strategies that achieve full coverage, but also produce good coverage frequency and visitation times. Policies that provide theoretical guarantees for these quantities have received some attention, but gaps have remained. We present: 1) A summary of how to achieve coverage by building a triangulation of the workspace, and the ensuing properties. 2) A description of simple local policies (LRV, for Least Recently Visited and LFV, for Least Frequently Visited) for achieving coverage by the patrolling robots. 3) New analytical arguments why different versions of LRV may require worst case exponential time between visits of triangles. 4) Analytical evidence that a local implementation of LFV on the edges of the dual graph is possible in our scenario, and immensely better in the worst case. 5) Experimental and simulation validation for the practical usefulness of these policies, showing that even a small number of weak robots with weak local information can greatly outperform a single, powerful robots with full information and computational capabilities.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge