Two-Stage Predict+Optimize for Mixed Integer Linear Programs with Unknown Parameters in Constraints

Consider the setting of constrained optimization, with some parameters unknown at solving time and requiring prediction from relevant features. Predict+Optimize is a recent framework for end-to-end training supervised learning models for such predictions, incorporating information about the optimization problem in the training process in order to yield better predictions in terms of the quality of the predicted solution under the true parameters. Almost all prior works have focused on the special case where the unknowns appear only in the optimization objective and not the constraints. Hu et al.~proposed the first adaptation of Predict+Optimize to handle unknowns appearing in constraints, but the framework has somewhat ad-hoc elements, and they provided a training algorithm only for covering and packing linear programs. In this work, we give a new \emph{simpler} and \emph{more powerful} framework called \emph{Two-Stage Predict+Optimize}, which we believe should be the canonical framework for the Predict+Optimize setting. We also give a training algorithm usable for all mixed integer linear programs, vastly generalizing the applicability of the framework. Experimental results demonstrate the superior prediction performance of our training framework over all classical and state-of-the-art methods.

Branch & Learn with Post-hoc Correction for Predict+Optimize with Unknown Parameters in Constraints

Combining machine learning and constrained optimization, Predict+Optimize tackles optimization problems containing parameters that are unknown at the time of solving. Prior works focus on cases with unknowns only in the objectives. A new framework was recently proposed to cater for unknowns also in constraints by introducing a loss function, called Post-hoc Regret, that takes into account the cost of correcting an unsatisfiable prediction. Since Post-hoc Regret is non-differentiable, the previous work computes only its approximation. While the notion of Post-hoc Regret is general, its specific implementation is applicable to only packing and covering linear programming problems. In this paper, we first show how to compute Post-hoc Regret exactly for any optimization problem solvable by a recursive algorithm satisfying simple conditions. Experimentation demonstrates substantial improvement in the quality of solutions as compared to the earlier approximation approach. Furthermore, we show experimentally the empirical behavior of different combinations of correction and penalty functions used in the Post-hoc Regret of the same benchmarks. Results provide insights for defining the appropriate Post-hoc Regret in different application scenarios.

Predict+Optimize for Packing and Covering LPs with Unknown Parameters in Constraints

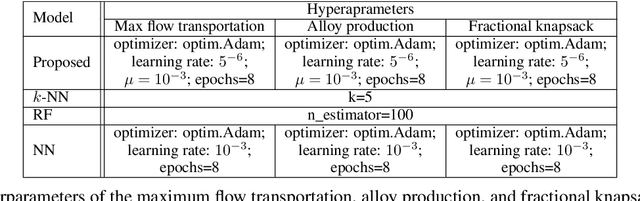
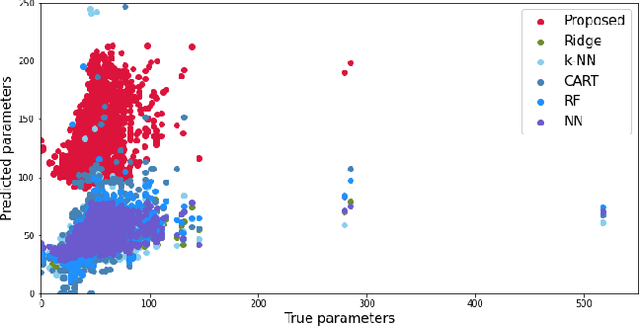
Predict+Optimize is a recently proposed framework which combines machine learning and constrained optimization, tackling optimization problems that contain parameters that are unknown at solving time. The goal is to predict the unknown parameters and use the estimates to solve for an estimated optimal solution to the optimization problem. However, all prior works have focused on the case where unknown parameters appear only in the optimization objective and not the constraints, for the simple reason that if the constraints were not known exactly, the estimated optimal solution might not even be feasible under the true parameters. The contributions of this paper are two-fold. First, we propose a novel and practically relevant framework for the Predict+Optimize setting, but with unknown parameters in both the objective and the constraints. We introduce the notion of a correction function, and an additional penalty term in the loss function, modelling practical scenarios where an estimated optimal solution can be modified into a feasible solution after the true parameters are revealed, but at an additional cost. Second, we propose a corresponding algorithmic approach for our framework, which handles all packing and covering linear programs. Our approach is inspired by the prior work of Mandi and Guns, though with crucial modifications and re-derivations for our very different setting. Experimentation demonstrates the superior empirical performance of our method over classical approaches.

iExam: A Novel Online Exam Monitoring and Analysis System Based on Face Detection and Recognition

Online exams via video conference software like Zoom have been adopted in many schools due to COVID-19. While it is convenient, it is challenging for teachers to supervise online exams from simultaneously displayed student Zoom windows. In this paper, we propose iExam, an intelligent online exam monitoring and analysis system that can not only use face detection to assist invigilators in real-time student identification, but also be able to detect common abnormal behaviors (including face disappearing, rotating faces, and replacing with a different person during the exams) via a face recognition-based post-exam video analysis. To build such a novel system in its first kind, we overcome three challenges. First, we discover a lightweight approach to capturing exam video streams and analyzing them in real time. Second, we utilize the left-corner names that are displayed on each student's Zoom window and propose an improved OCR (optical character recognition) technique to automatically gather the ground truth for the student faces with dynamic positions. Third, we perform several experimental comparisons and optimizations to efficiently shorten the training and testing time required on teachers' PC. Our evaluation shows that iExam achieves high accuracy, 90.4% for real-time face detection and 98.4% for post-exam face recognition, while maintaining acceptable runtime performance. We have made iExam's source code available at https://github.com/VPRLab/iExam.

Branch & Learn for Recursively and Iteratively Solvable Problems in Predict+Optimize

This paper proposes Branch & Learn, a framework for Predict+Optimize to tackle optimization problems containing parameters that are unknown at the time of solving. Given an optimization problem solvable by a recursive algorithm satisfying simple conditions, we show how a corresponding learning algorithm can be constructed directly and methodically from the recursive algorithm. Our framework applies also to iterative algorithms by viewing them as a degenerate form of recursion. Extensive experimentation shows better performance for our proposal over classical and state-of-the-art approaches.

Augmenting Stream Constraint Programming with Eventuality Conditions

Stream constraint programming is a recent addition to the family of constraint programming frameworks, where variable domains are sets of infinite streams over finite alphabets. Previous works showed promising results for its applicability to real-world planning and control problems. In this paper, motivated by the modelling of planning applications, we improve the expressiveness of the framework by introducing 1) the "until" constraint, a new construct that is adapted from Linear Temporal Logic and 2) the @ operator on streams, a syntactic sugar for which we provide a more efficient solving algorithm over simple desugaring. For both constructs, we propose corresponding novel solving algorithms and prove their correctness. We present competitive experimental results on the Missionaries and Cannibals logic puzzle and a standard path planning application on the grid, by comparing with Apt and Brand's method for verifying eventuality conditions using a CP approach.

Tractability and Decompositions of Global Cost Functions

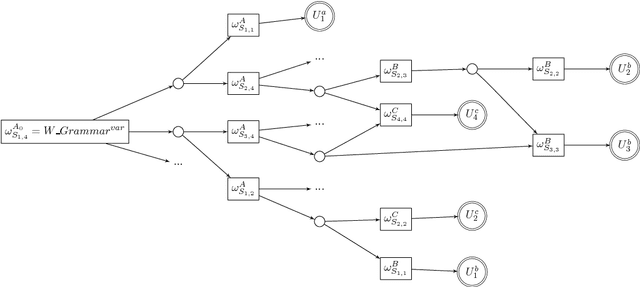
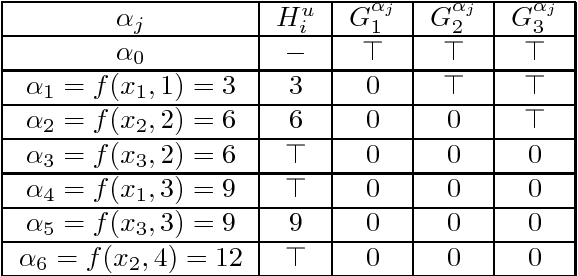
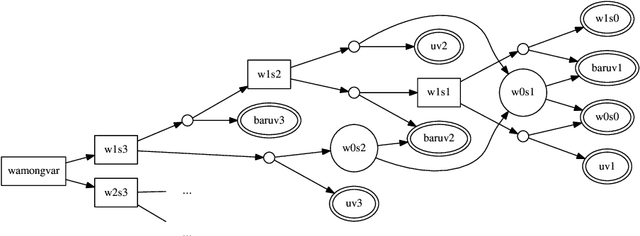
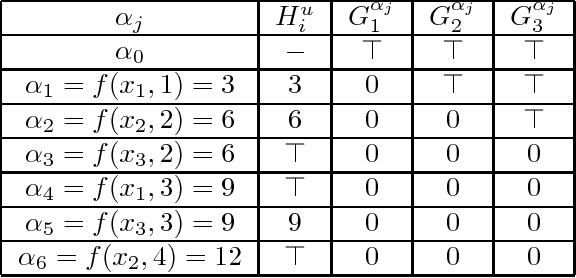
Enforcing local consistencies in cost function networks is performed by applying so-called Equivalent Preserving Transformations (EPTs) to the cost functions. As EPTs transform the cost functions, they may break the property that was making local consistency enforcement tractable on a global cost function. A global cost function is called tractable projection-safe when applying an EPT to it is tractable and does not break the tractability property. In this paper, we prove that depending on the size r of the smallest scopes used for performing EPTs, the tractability of global cost functions can be preserved (r = 0) or destroyed (r > 1). When r = 1, the answer is indefinite. We show that on a large family of cost functions, EPTs can be computed via dynamic programming-based algorithms, leading to tractable projection-safety. We also show that when a global cost function can be decomposed into a Berge acyclic network of bounded arity cost functions, soft local consistencies such as soft Directed or Virtual Arc Consistency can directly emulate dynamic programming. These different approaches to decomposable cost functions are then embedded in a solver for extensive experiments that confirm the feasibility and efficiency of our proposal.