Super-Reparametrizations of Weighted CSPs: Properties and Optimization Perspective

The notion of reparametrizations of Weighted CSPs (WCSPs) (also known as equivalence-preserving transformations of WCSPs) is well-known and finds its use in many algorithms to approximate or bound the optimal WCSP value. In contrast, the concept of super-reparametrizations (which are changes of the weights that keep or increase the WCSP objective for every assignment) was already proposed but never studied in detail. To fill this gap, we present a number of theoretical properties of super-reparametrizations and compare them to those of reparametrizations. Furthermore, we propose a framework for computing upper bounds on the optimal value of the (maximization version of) WCSP using super-reparametrizations. We show that it is in principle possible to employ arbitrary (under some technical conditions) constraint propagation rules to improve the bound. For arc consistency in particular, the method reduces to the known Virtual AC (VAC) algorithm. Newly, we implemented the method for singleton arc consistency (SAC) and compared it to other strong local consistencies in WCSPs on a public benchmark. The results show that the bounds obtained from SAC are superior for many instance groups.

Improved Acyclicity Reasoning for Bayesian Network Structure Learning with Constraint Programming

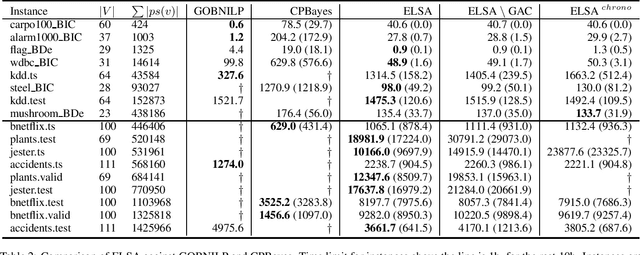
Bayesian networks are probabilistic graphical models with a wide range of application areas including gene regulatory networks inference, risk analysis and image processing. Learning the structure of a Bayesian network (BNSL) from discrete data is known to be an NP-hard task with a superexponential search space of directed acyclic graphs. In this work, we propose a new polynomial time algorithm for discovering a subset of all possible cluster cuts, a greedy algorithm for approximately solving the resulting linear program, and a generalised arc consistency algorithm for the acyclicity constraint. We embed these in the constraint programmingbased branch-and-bound solver CPBayes and show that, despite being suboptimal, they improve performance by orders of magnitude. The resulting solver also compares favourably with GOBNILP, a state-of-the-art solver for the BNSL problem which solves an NP-hard problem to discover each cut and solves the linear program exactly.

Exact and approximate inference in graphical models: variable elimination and beyond

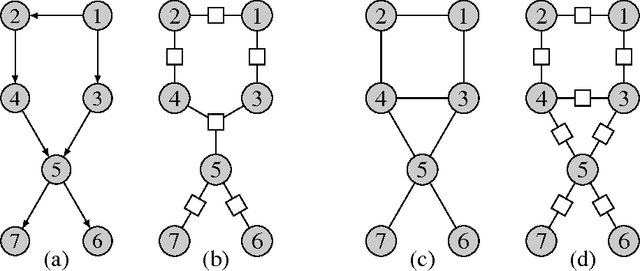
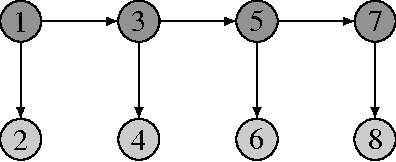
Probabilistic graphical models offer a powerful framework to account for the dependence structure between variables, which is represented as a graph. However, the dependence between variables may render inference tasks intractable. In this paper we review techniques exploiting the graph structure for exact inference, borrowed from optimisation and computer science. They are built on the principle of variable elimination whose complexity is dictated in an intricate way by the order in which variables are eliminated. The so-called treewidth of the graph characterises this algorithmic complexity: low-treewidth graphs can be processed efficiently. The first message that we illustrate is therefore the idea that for inference in graphical model, the number of variables is not the limiting factor, and it is worth checking for the treewidth before turning to approximate methods. We show how algorithms providing an upper bound of the treewidth can be exploited to derive a 'good' elimination order enabling to perform exact inference. The second message is that when the treewidth is too large, algorithms for approximate inference linked to the principle of variable elimination, such as loopy belief propagation and variational approaches, can lead to accurate results while being much less time consuming than Monte-Carlo approaches. We illustrate the techniques reviewed in this article on benchmarks of inference problems in genetic linkage analysis and computer vision, as well as on hidden variables restoration in coupled Hidden Markov Models.

Tractability and Decompositions of Global Cost Functions

Enforcing local consistencies in cost function networks is performed by applying so-called Equivalent Preserving Transformations (EPTs) to the cost functions. As EPTs transform the cost functions, they may break the property that was making local consistency enforcement tractable on a global cost function. A global cost function is called tractable projection-safe when applying an EPT to it is tractable and does not break the tractability property. In this paper, we prove that depending on the size r of the smallest scopes used for performing EPTs, the tractability of global cost functions can be preserved (r = 0) or destroyed (r > 1). When r = 1, the answer is indefinite. We show that on a large family of cost functions, EPTs can be computed via dynamic programming-based algorithms, leading to tractable projection-safety. We also show that when a global cost function can be decomposed into a Berge acyclic network of bounded arity cost functions, soft local consistencies such as soft Directed or Virtual Arc Consistency can directly emulate dynamic programming. These different approaches to decomposable cost functions are then embedded in a solver for extensive experiments that confirm the feasibility and efficiency of our proposal.

Bounds Arc Consistency for Weighted CSPs

The Weighted Constraint Satisfaction Problem (WCSP) framework allows representing and solving problems involving both hard constraints and cost functions. It has been applied to various problems, including resource allocation, bioinformatics, scheduling, etc. To solve such problems, solvers usually rely on branch-and-bound algorithms equipped with local consistency filtering, mostly soft arc consistency. However, these techniques are not well suited to solve problems with very large domains. Motivated by the resolution of an RNA gene localization problem inside large genomic sequences, and in the spirit of bounds consistency for large domains in crisp CSPs, we introduce soft bounds arc consistency, a new weighted local consistency specifically designed for WCSP with very large domains. Compared to soft arc consistency, BAC provides significantly improved time and space asymptotic complexity. In this paper, we show how the semantics of cost functions can be exploited to further improve the time complexity of BAC. We also compare both in theory and in practice the efficiency of BAC on a WCSP with bounds consistency enforced on a crisp CSP using cost variables. On two different real problems modeled as WCSP, including our RNA gene localization problem, we observe that maintaining bounds arc consistency outperforms arc consistency and also improves over bounds consistency enforced on a constraint model with cost variables.

A Logical Approach to Efficient Max-SAT solving

Weighted Max-SAT is the optimization version of SAT and many important problems can be naturally encoded as such. Solving weighted Max-SAT is an important problem from both a theoretical and a practical point of view. In recent years, there has been considerable interest in finding efficient solving techniques. Most of this work focus on the computation of good quality lower bounds to be used within a branch and bound DPLL-like algorithm. Most often, these lower bounds are described in a procedural way. Because of that, it is difficult to realize the {\em logic} that is behind. In this paper we introduce an original framework for Max-SAT that stresses the parallelism with classical SAT. Then, we extend the two basic SAT solving techniques: {\em search} and {\em inference}. We show that many algorithmic {\em tricks} used in state-of-the-art Max-SAT solvers are easily expressable in {\em logic} terms with our framework in a unified manner. Besides, we introduce an original search algorithm that performs a restricted amount of {\em weighted resolution} at each visited node. We empirically compare our algorithm with a variety of solving alternatives on several benchmarks. Our experiments, which constitute to the best of our knowledge the most comprehensive Max-sat evaluation ever reported, show that our algorithm is generally orders of magnitude faster than any competitor.