Improved Acyclicity Reasoning for Bayesian Network Structure Learning with Constraint Programming

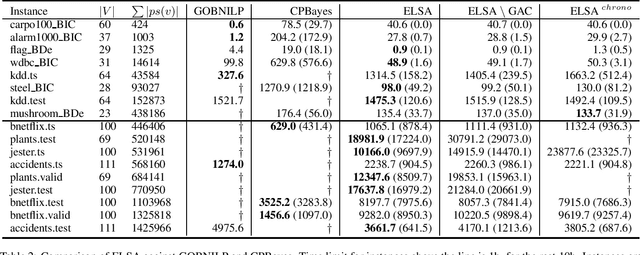
Bayesian networks are probabilistic graphical models with a wide range of application areas including gene regulatory networks inference, risk analysis and image processing. Learning the structure of a Bayesian network (BNSL) from discrete data is known to be an NP-hard task with a superexponential search space of directed acyclic graphs. In this work, we propose a new polynomial time algorithm for discovering a subset of all possible cluster cuts, a greedy algorithm for approximately solving the resulting linear program, and a generalised arc consistency algorithm for the acyclicity constraint. We embed these in the constraint programmingbased branch-and-bound solver CPBayes and show that, despite being suboptimal, they improve performance by orders of magnitude. The resulting solver also compares favourably with GOBNILP, a state-of-the-art solver for the BNSL problem which solves an NP-hard problem to discover each cut and solves the linear program exactly.