Computational Complexity of Three Central Problems in Itemset Mining

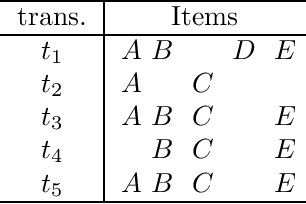
Itemset mining is one of the most studied tasks in knowledge discovery. In this paper we analyze the computational complexity of three central itemset mining problems. We prove that mining confident rules with a given item in the head is NP-hard. We prove that mining high utility itemsets is NP-hard. We finally prove that mining maximal or closed itemsets is coNP-hard as soon as the users can specify constraints on the kind of itemsets they are interested in.

Partial Queries for Constraint Acquisition

Learning constraint networks is known to require a number of membership queries exponential in the number of variables. In this paper, we learn constraint networks by asking the user partial queries. That is, we ask the user to classify assignments to subsets of the variables as positive or negative. We provide an algorithm, called QUACQ, that, given a negative example, focuses onto a constraint of the target network in a number of queries logarithmic in the size of the example. The whole constraint network can then be learned with a polynomial number of partial queries. We give information theoretic lower bounds for learning some simple classes of constraint networks and show that our generic algorithm is optimal in some cases.

Sketched Answer Set Programming

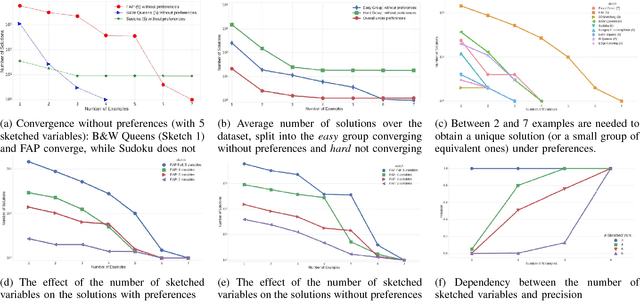
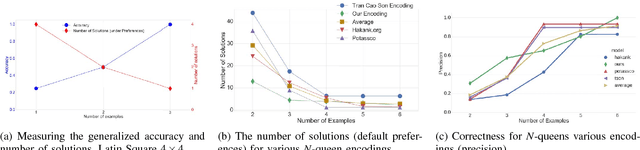
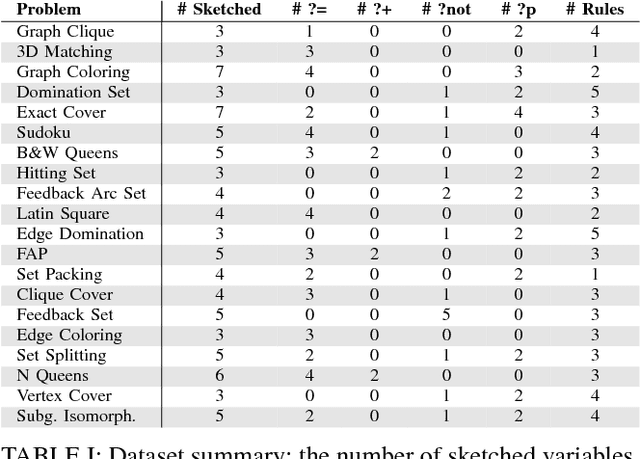
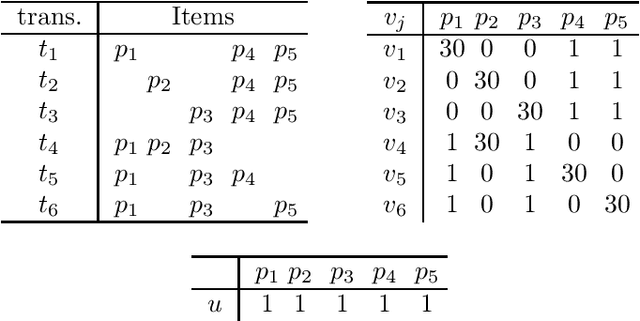
Answer Set Programming (ASP) is a powerful modeling formalism for combinatorial problems. However, writing ASP models is not trivial. We propose a novel method, called Sketched Answer Set Programming (SkASP), aiming at supporting the user in resolving this issue. The user writes an ASP program while marking uncertain parts open with question marks. In addition, the user provides a number of positive and negative examples of the desired program behaviour. The sketched model is rewritten into another ASP program, which is solved by traditional methods. As a result, the user obtains a functional and reusable ASP program modelling her problem. We evaluate our approach on 21 well known puzzles and combinatorial problems inspired by Karp's 21 NP-complete problems and demonstrate a use-case for a database application based on ASP.

Users Constraints in Itemset Mining

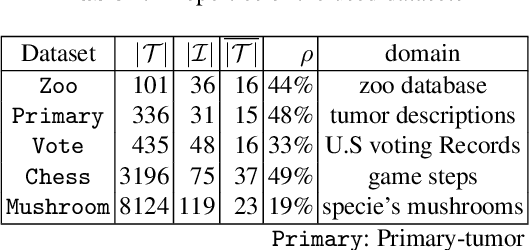
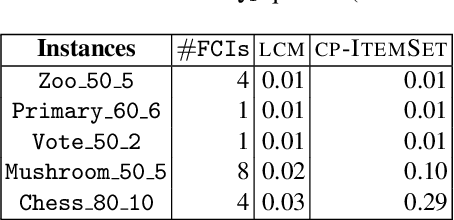
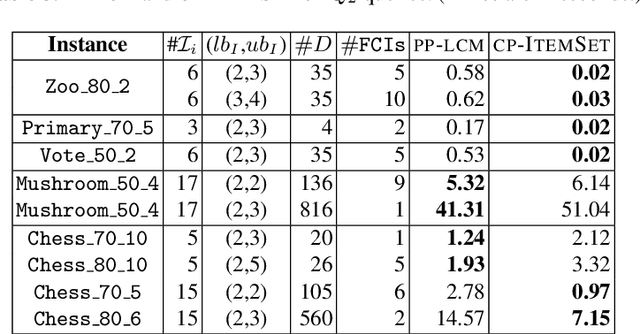
Discovering significant itemsets is one of the fundamental problems in data mining. It has recently been shown that constraint programming is a flexible way to tackle data mining tasks. With a constraint programming approach, we can easily express and efficiently answer queries with users constraints on items. However, in many practical cases it is possible that queries also express users constraints on the dataset itself. For instance, asking for a particular itemset in a particular part of the dataset. This paper presents a general constraint programming model able to handle any kind of query on the items or the dataset for itemset mining.

Tractability and Decompositions of Global Cost Functions

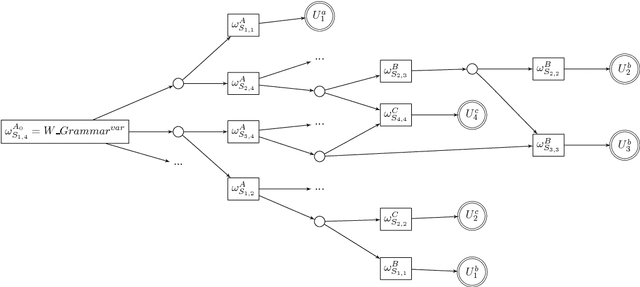
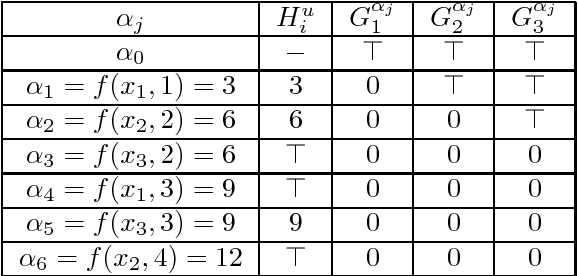
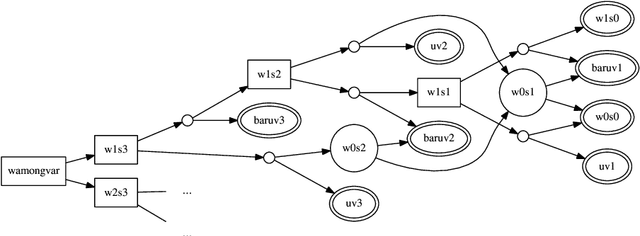
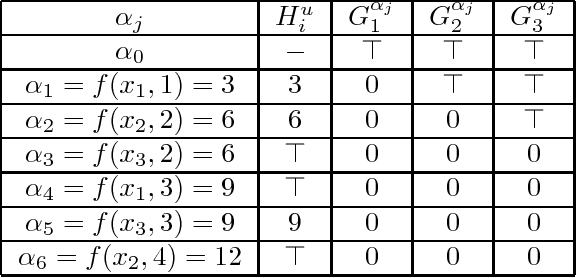
Enforcing local consistencies in cost function networks is performed by applying so-called Equivalent Preserving Transformations (EPTs) to the cost functions. As EPTs transform the cost functions, they may break the property that was making local consistency enforcement tractable on a global cost function. A global cost function is called tractable projection-safe when applying an EPT to it is tractable and does not break the tractability property. In this paper, we prove that depending on the size r of the smallest scopes used for performing EPTs, the tractability of global cost functions can be preserved (r = 0) or destroyed (r > 1). When r = 1, the answer is indefinite. We show that on a large family of cost functions, EPTs can be computed via dynamic programming-based algorithms, leading to tractable projection-safety. We also show that when a global cost function can be decomposed into a Berge acyclic network of bounded arity cost functions, soft local consistencies such as soft Directed or Virtual Arc Consistency can directly emulate dynamic programming. These different approaches to decomposable cost functions are then embedded in a solver for extensive experiments that confirm the feasibility and efficiency of our proposal.

The Inductive Constraint Programming Loop

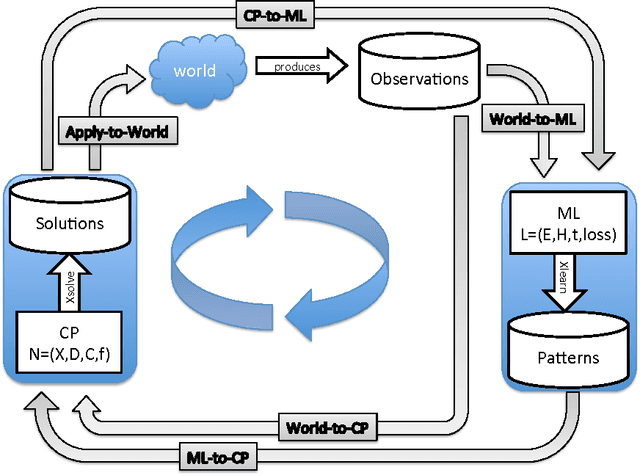
Constraint programming is used for a variety of real-world optimisation problems, such as planning, scheduling and resource allocation problems. At the same time, one continuously gathers vast amounts of data about these problems. Current constraint programming software does not exploit such data to update schedules, resources and plans. We propose a new framework, that we call the Inductive Constraint Programming loop. In this approach data is gathered and analyzed systematically, in order to dynamically revise and adapt constraints and optimization criteria. Inductive Constraint Programming aims at bridging the gap between the areas of data mining and machine learning on the one hand, and constraint programming on the other hand.

The AllDifferent Constraint with Precedences

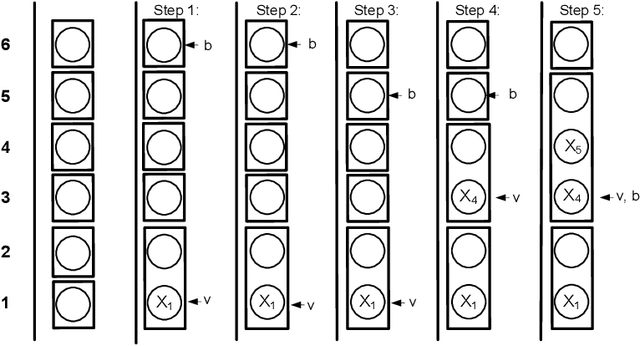
We propose AllDiffPrecedence, a new global constraint that combines together an AllDifferent constraint with precedence constraints that strictly order given pairs of variables. We identify a number of applications for this global constraint including instruction scheduling and symmetry breaking. We give an efficient propagation algorithm that enforces bounds consistency on this global constraint. We show how to implement this propagator using a decomposition that extends the bounds consistency enforcing decomposition proposed for the AllDifferent constraint. Finally, we prove that enforcing domain consistency on this global constraint is NP-hard in general.

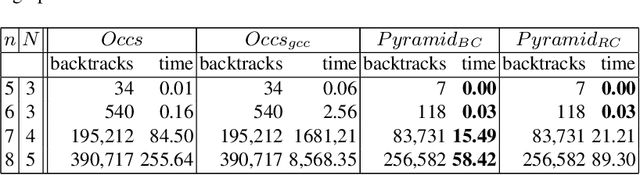
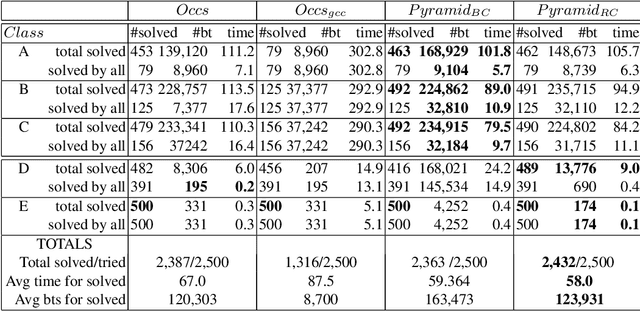
Decomposition of the NVALUE constraint

We study decompositions of the global NVALUE constraint. Our main contribution is theoretical: we show that there are propagators for global constraints like NVALUE which decomposition can simulate with the same time complexity but with a much greater space complexity. This suggests that the benefit of a global propagator may often not be in saving time but in saving space. Our other theoretical contribution is to show for the first time that range consistency can be enforced on NVALUE with the same worst-case time complexity as bound consistency. Finally, the decompositions we study are readily encoded as linear inequalities. We are therefore able to use them in integer linear programs.

Propagating Conjunctions of AllDifferent Constraints

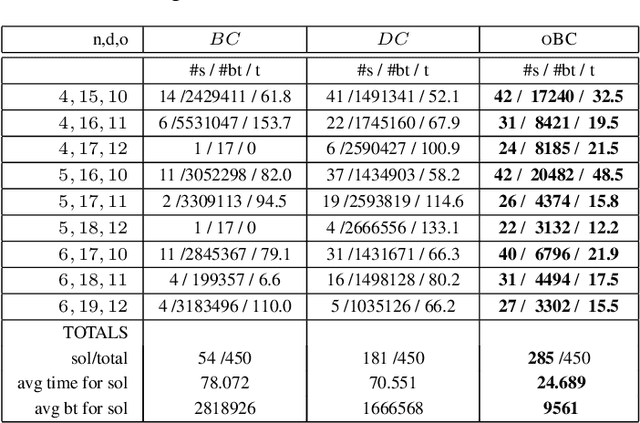
We study propagation algorithms for the conjunction of two AllDifferent constraints. Solutions of an AllDifferent constraint can be seen as perfect matchings on the variable/value bipartite graph. Therefore, we investigate the problem of finding simultaneous bipartite matchings. We present an extension of the famous Hall theorem which characterizes when simultaneous bipartite matchings exists. Unfortunately, finding such matchings is NP-hard in general. However, we prove a surprising result that finding a simultaneous matching on a convex bipartite graph takes just polynomial time. Based on this theoretical result, we provide the first polynomial time bound consistency algorithm for the conjunction of two AllDifferent constraints. We identify a pathological problem on which this propagator is exponentially faster compared to existing propagators. Our experiments show that this new propagator can offer significant benefits over existing methods.

Circuit Complexity and Decompositions of Global Constraints

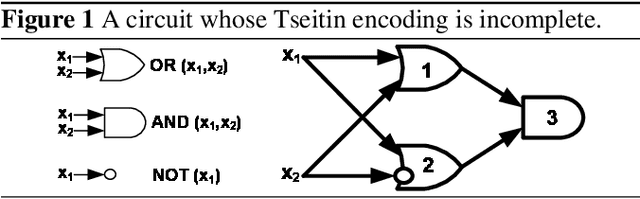
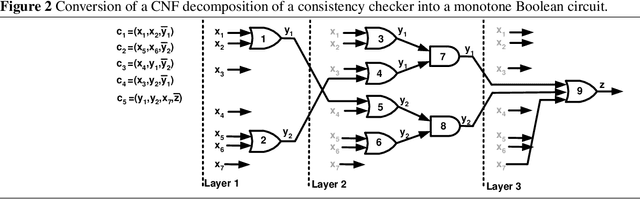
We show that tools from circuit complexity can be used to study decompositions of global constraints. In particular, we study decompositions of global constraints into conjunctive normal form with the property that unit propagation on the decomposition enforces the same level of consistency as a specialized propagation algorithm. We prove that a constraint propagator has a a polynomial size decomposition if and only if it can be computed by a polynomial size monotone Boolean circuit. Lower bounds on the size of monotone Boolean circuits thus translate to lower bounds on the size of decompositions of global constraints. For instance, we prove that there is no polynomial sized decomposition of the domain consistency propagator for the ALLDIFFERENT constraint.