Dimosthenis C. Tsouros
Efficient Multiple Constraint Acquisition
Sep 13, 2021

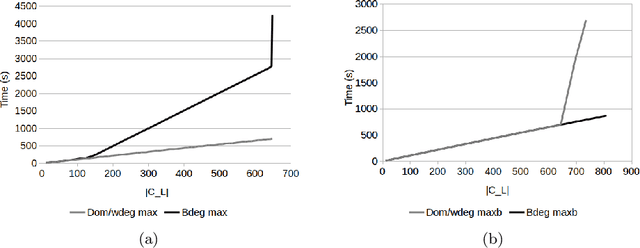
Abstract:Constraint acquisition systems such as QuAcq and MultiAcq can assist non-expert users to model their problems as constraint networks by classifying (partial) examples as positive or negative. For each negative example, the former focuses on one constraint of the target network, while the latter can learn a maximum number of constraints. Two bottlenecks of the acquisition process where both these algorithms encounter problems are the large number of queries required to reach convergence, and the high cpu times needed to generate queries, especially near convergence. In this paper we propose algorithmic and heuristic methods to deal with both these issues. We first describe an algorithm, called MQuAcq, that blends the main idea of MultiAcq into QuAcq resulting in a method that learns as many constraints as MultiAcq does after a negative example, but with a lower complexity. A detailed theoretical analysis of the proposed algorithm is also presented. %We also present a technique that boosts the performance of constraint acquisition by reducing the number of queries significantly. Then we turn our attention to query generation which is a significant but rather overlooked part of the acquisition process. We describe %in detail how query generation in a typical constraint acquisition system operates, and we propose heuristics for improving its efficiency. Experiments from various domains demonstrate that our resulting algorithm that integrates all the new techniques does not only generate considerably fewer queries than QuAcq and MultiAcq, but it is also by far faster than both of them, in average query generation time as well as in total run time, and also largely alleviates the premature convergence problem.
Partial Queries for Constraint Acquisition
Mar 14, 2020
Abstract:Learning constraint networks is known to require a number of membership queries exponential in the number of variables. In this paper, we learn constraint networks by asking the user partial queries. That is, we ask the user to classify assignments to subsets of the variables as positive or negative. We provide an algorithm, called QUACQ, that, given a negative example, focuses onto a constraint of the target network in a number of queries logarithmic in the size of the example. The whole constraint network can then be learned with a polynomial number of partial queries. We give information theoretic lower bounds for learning some simple classes of constraint networks and show that our generic algorithm is optimal in some cases.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge