Scalable Coupling of Deep Learning with Logical Reasoning
Paper and Code
May 12, 2023
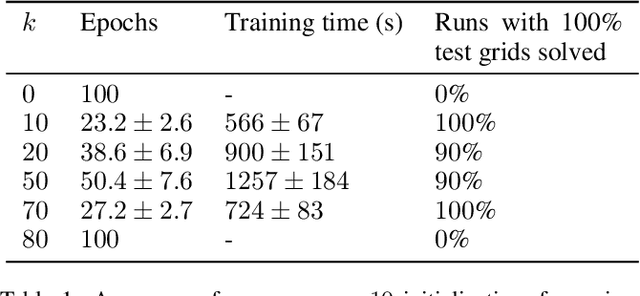


In the ongoing quest for hybridizing discrete reasoning with neural nets, there is an increasing interest in neural architectures that can learn how to solve discrete reasoning or optimization problems from natural inputs. In this paper, we introduce a scalable neural architecture and loss function dedicated to learning the constraints and criteria of NP-hard reasoning problems expressed as discrete Graphical Models. Our loss function solves one of the main limitations of Besag's pseudo-loglikelihood, enabling learning of high energies. We empirically show it is able to efficiently learn how to solve NP-hard reasoning problems from natural inputs as the symbolic, visual or many-solutions Sudoku problems as well as the energy optimization formulation of the protein design problem, providing data efficiency, interpretability, and \textit{a posteriori} control over predictions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge