On The Complexity and Completeness of Static Constraints for Breaking Row and Column Symmetry
Paper and Code
Jul 05, 2010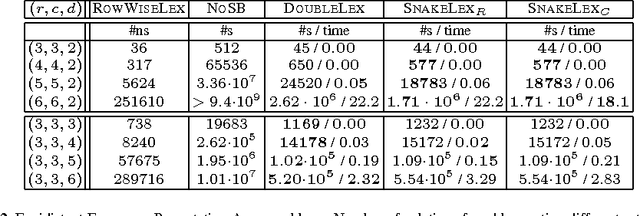
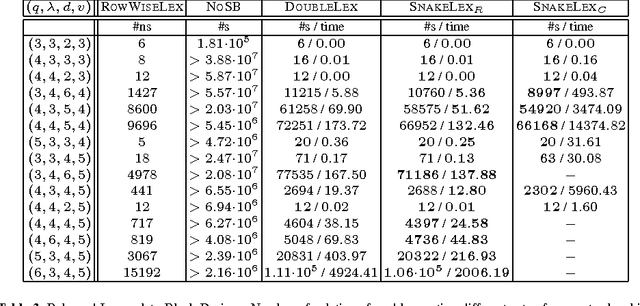
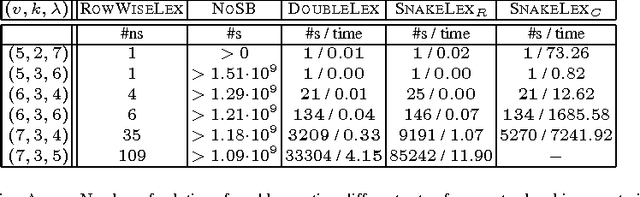
We consider a common type of symmetry where we have a matrix of decision variables with interchangeable rows and columns. A simple and efficient method to deal with such row and column symmetry is to post symmetry breaking constraints like DOUBLELEX and SNAKELEX. We provide a number of positive and negative results on posting such symmetry breaking constraints. On the positive side, we prove that we can compute in polynomial time a unique representative of an equivalence class in a matrix model with row and column symmetry if the number of rows (or of columns) is bounded and in a number of other special cases. On the negative side, we show that whilst DOUBLELEX and SNAKELEX are often effective in practice, they can leave a large number of symmetric solutions in the worst case. In addition, we prove that propagating DOUBLELEX completely is NP-hard. Finally we consider how to break row, column and value symmetry, correcting a result in the literature about the safeness of combining different symmetry breaking constraints. We end with the first experimental study on how much symmetry is left by DOUBLELEX and SNAKELEX on some benchmark problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge