Joao Marques-Silva
ICREA, University of Lleida, Spain
On Trustworthy Rule-Based Models and Explanations
Jul 10, 2025Abstract:A task of interest in machine learning (ML) is that of ascribing explanations to the predictions made by ML models. Furthermore, in domains deemed high risk, the rigor of explanations is paramount. Indeed, incorrect explanations can and will mislead human decision makers. As a result, and even if interpretability is acknowledged as an elusive concept, so-called interpretable models are employed ubiquitously in high-risk uses of ML and data mining (DM). This is the case for rule-based ML models, which encompass decision trees, diagrams, sets and lists. This paper relates explanations with well-known undesired facets of rule-based ML models, which include negative overlap and several forms of redundancy. The paper develops algorithms for the analysis of these undesired facets of rule-based systems, and concludes that well-known and widely used tools for learning rule-based ML models will induce rule sets that exhibit one or more negative facets.
Most General Explanations of Tree Ensembles
May 19, 2025Abstract:Explainable Artificial Intelligence (XAI) is critical for attaining trust in the operation of AI systems. A key question of an AI system is ``why was this decision made this way''. Formal approaches to XAI use a formal model of the AI system to identify abductive explanations. While abductive explanations may be applicable to a large number of inputs sharing the same concrete values, more general explanations may be preferred for numeric inputs. So-called inflated abductive explanations give intervals for each feature ensuring that any input whose values fall withing these intervals is still guaranteed to make the same prediction. Inflated explanations cover a larger portion of the input space, and hence are deemed more general explanations. But there can be many (inflated) abductive explanations for an instance. Which is the best? In this paper, we show how to find a most general abductive explanation for an AI decision. This explanation covers as much of the input space as possible, while still being a correct formal explanation of the model's behaviour. Given that we only want to give a human one explanation for a decision, the most general explanation gives us the explanation with the broadest applicability, and hence the one most likely to seem sensible. (The paper has been accepted at IJCAI2025 conference.)
The Explanation Game -- Rekindled (Extended Version)
Jan 20, 2025
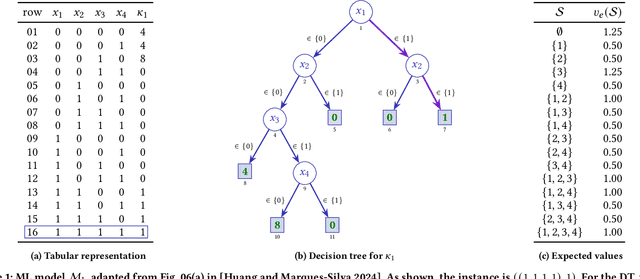

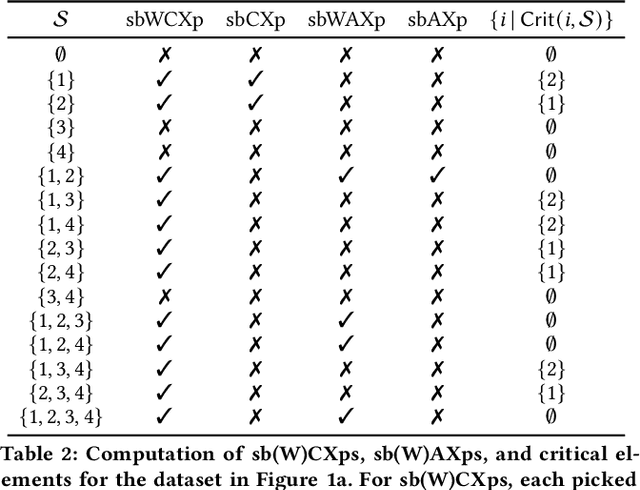
Abstract:Recent work demonstrated the existence of critical flaws in the current use of Shapley values in explainable AI (XAI), i.e. the so-called SHAP scores. These flaws are significant in that the scores provided to a human decision-maker can be misleading. Although these negative results might appear to indicate that Shapley values ought not be used in XAI, this paper argues otherwise. Concretely, this paper proposes a novel definition of SHAP scores that overcomes existing flaws. Furthermore, the paper outlines a practically efficient solution for the rigorous estimation of the novel SHAP scores. Preliminary experimental results confirm our claims, and further underscore the flaws of the current SHAP scores.
Efficient Contrastive Explanations on Demand
Dec 24, 2024Abstract:Recent work revealed a tight connection between adversarial robustness and restricted forms of symbolic explanations, namely distance-based (formal) explanations. This connection is significant because it represents a first step towards making the computation of symbolic explanations as efficient as deciding the existence of adversarial examples, especially for highly complex machine learning (ML) models. However, a major performance bottleneck remains, because of the very large number of features that ML models may possess, in particular for deep neural networks. This paper proposes novel algorithms to compute the so-called contrastive explanations for ML models with a large number of features, by leveraging on adversarial robustness. Furthermore, the paper also proposes novel algorithms for listing explanations and finding smallest contrastive explanations. The experimental results demonstrate the performance gains achieved by the novel algorithms proposed in this paper.
SHAP scores fail pervasively even when Lipschitz succeeds
Dec 18, 2024Abstract:The ubiquitous use of Shapley values in eXplainable AI (XAI) has been triggered by the tool SHAP, and as a result are commonly referred to as SHAP scores. Recent work devised examples of machine learning (ML) classifiers for which the computed SHAP scores are thoroughly unsatisfactory, by allowing human decision-makers to be misled. Nevertheless, such examples could be perceived as somewhat artificial, since the selected classes must be interpreted as numeric. Furthermore, it was unclear how general were the issues identified with SHAP scores. This paper answers these criticisms. First, the paper shows that for Boolean classifiers there are arbitrarily many examples for which the SHAP scores must be deemed unsatisfactory. Second, the paper shows that the issues with SHAP scores are also observed in the case of regression models. In addition, the paper studies the class of regression models that respect Lipschitz continuity, a measure of a function's rate of change that finds important recent uses in ML, including model robustness. Concretely, the paper shows that the issues with SHAP scores occur even for regression models that respect Lipschitz continuity. Finally, the paper shows that the same issues are guaranteed to exist for arbitrarily differentiable regression models.
The Sets of Power
Oct 10, 2024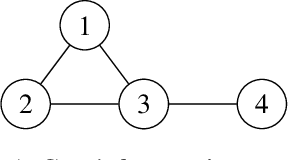
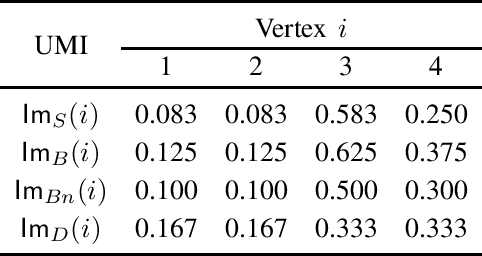
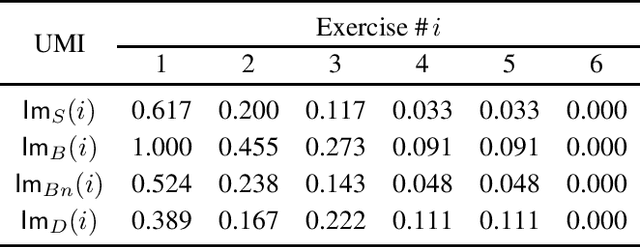
Abstract:Measures of voting power have been the subject of extensive research since the mid 1940s. More recently, similar measures of relative importance have been studied in other domains that include inconsistent knowledge bases, intensity of attacks in argumentation, different problems in the analysis of database management, and explainability. This paper demonstrates that all these examples are instantiations of computing measures of importance for a rather more general problem domain. The paper then shows that the best-known measures of importance can be computed for any reference set whenever one is given a monotonically increasing predicate that partitions the subsets of that reference set. As a consequence, the paper also proves that measures of importance can be devised in several domains, for some of which such measures have not yet been studied nor proposed. Furthermore, the paper highlights several research directions related with computing measures of importance.
From SHAP Scores to Feature Importance Scores
May 20, 2024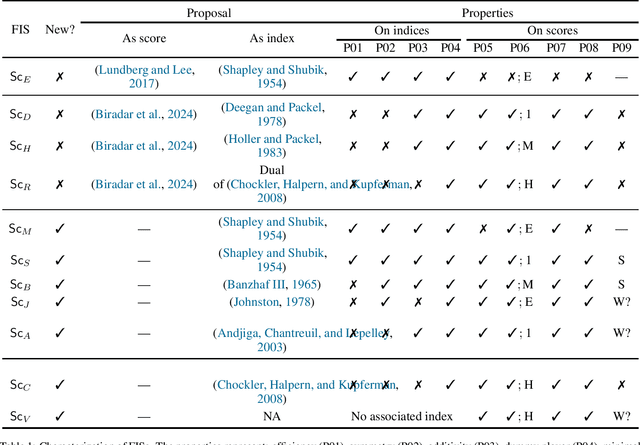
Abstract:A central goal of eXplainable Artificial Intelligence (XAI) is to assign relative importance to the features of a Machine Learning (ML) model given some prediction. The importance of this task of explainability by feature attribution is illustrated by the ubiquitous recent use of tools such as SHAP and LIME. Unfortunately, the exact computation of feature attributions, using the game-theoretical foundation underlying SHAP and LIME, can yield manifestly unsatisfactory results, that tantamount to reporting misleading relative feature importance. Recent work targeted rigorous feature attribution, by studying axiomatic aggregations of features based on logic-based definitions of explanations by feature selection. This paper shows that there is an essential relationship between feature attribution and a priori voting power, and that those recently proposed axiomatic aggregations represent a few instantiations of the range of power indices studied in the past. Furthermore, it remains unclear how some of the most widely used power indices might be exploited as feature importance scores (FISs), i.e. the use of power indices in XAI, and which of these indices would be the best suited for the purposes of XAI by feature attribution, namely in terms of not producing results that could be deemed as unsatisfactory. This paper proposes novel desirable properties that FISs should exhibit. In addition, the paper also proposes novel FISs exhibiting the proposed properties. Finally, the paper conducts a rigorous analysis of the best-known power indices in terms of the proposed properties.
Distance-Restricted Explanations: Theoretical Underpinnings & Efficient Implementation
May 14, 2024Abstract:The uses of machine learning (ML) have snowballed in recent years. In many cases, ML models are highly complex, and their operation is beyond the understanding of human decision-makers. Nevertheless, some uses of ML models involve high-stakes and safety-critical applications. Explainable artificial intelligence (XAI) aims to help human decision-makers in understanding the operation of such complex ML models, thus eliciting trust in their operation. Unfortunately, the majority of past XAI work is based on informal approaches, that offer no guarantees of rigor. Unsurprisingly, there exists comprehensive experimental and theoretical evidence confirming that informal methods of XAI can provide human-decision makers with erroneous information. Logic-based XAI represents a rigorous approach to explainability; it is model-based and offers the strongest guarantees of rigor of computed explanations. However, a well-known drawback of logic-based XAI is the complexity of logic reasoning, especially for highly complex ML models. Recent work proposed distance-restricted explanations, i.e. explanations that are rigorous provided the distance to a given input is small enough. Distance-restricted explainability is tightly related with adversarial robustness, and it has been shown to scale for moderately complex ML models, but the number of inputs still represents a key limiting factor. This paper investigates novel algorithms for scaling up the performance of logic-based explainers when computing and enumerating ML model explanations with a large number of inputs.
On Correcting SHAP Scores
Apr 30, 2024Abstract:Recent work uncovered examples of classifiers for which SHAP scores yield misleading feature attributions. While such examples might be perceived as suggesting the inadequacy of Shapley values for explainability, this paper shows that the source of the identified shortcomings of SHAP scores resides elsewhere. Concretely, the paper makes the case that the failings of SHAP scores result from the characteristic functions used in earlier works. Furthermore, the paper identifies a number of properties that characteristic functions ought to respect, and proposes several novel characteristic functions, each exhibiting one or more of the desired properties. More importantly, some of the characteristic functions proposed in this paper are guaranteed not to exhibit any of the shortcomings uncovered by earlier work. The paper also investigates the impact of the new characteristic functions on the complexity of computing SHAP scores. Finally, the paper proposes modifications to the tool SHAP to use instead one of our novel characteristic functions, thereby eliminating some of the limitations reported for SHAP scores.
Locally-Minimal Probabilistic Explanations
Dec 20, 2023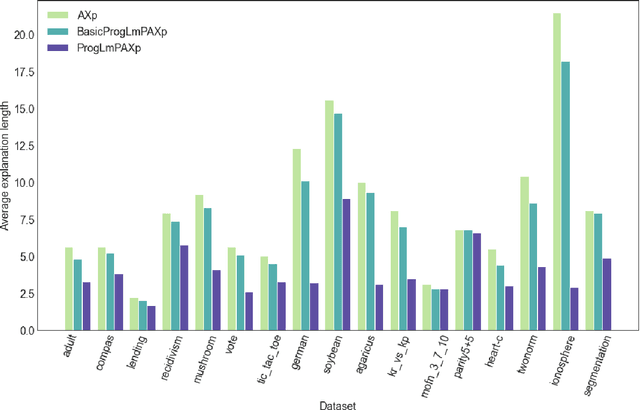
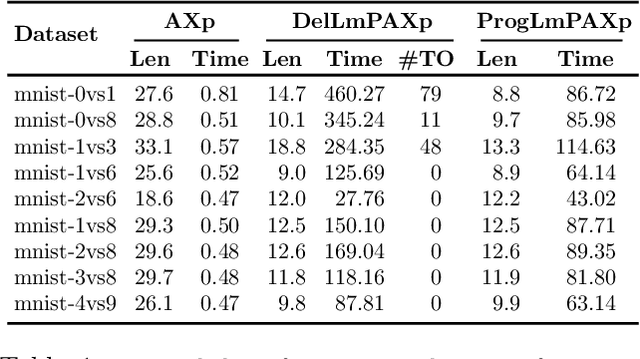
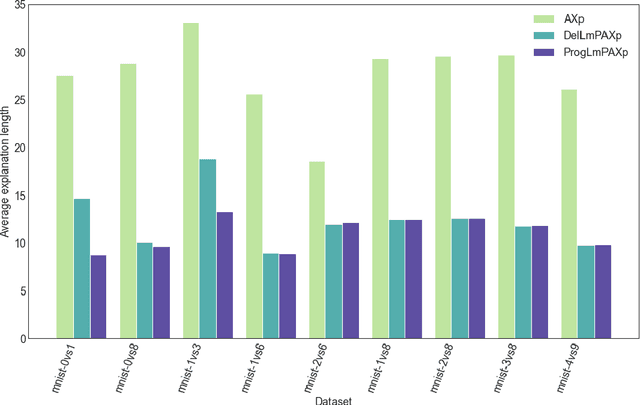
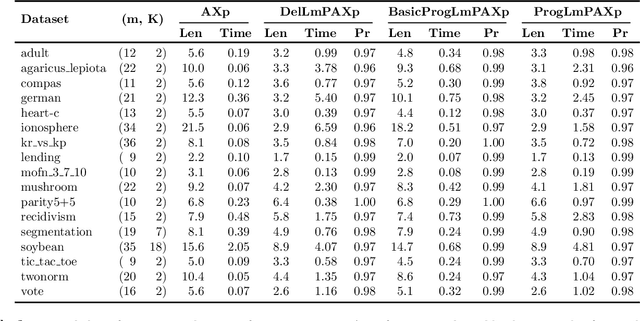
Abstract:Formal abductive explanations offer crucial guarantees of rigor and so are of interest in high-stakes uses of machine learning (ML). One drawback of abductive explanations is explanation size, justified by the cognitive limits of human decision-makers. Probabilistic abductive explanations (PAXps) address this limitation, but their theoretical and practical complexity makes their exact computation most often unrealistic. This paper proposes novel efficient algorithms for the computation of locally-minimal PXAps, which offer high-quality approximations of PXAps in practice. The experimental results demonstrate the practical efficiency of the proposed algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge