Model Counting in the Wild

Model counting is a fundamental problem in automated reasoning with applications in probabilistic inference, network reliability, neural network verification, and more. Although model counting is computationally intractable from a theoretical perspective due to its #P-completeness, the past decade has seen significant progress in developing state-of-the-art model counters to address scalability challenges. In this work, we conduct a rigorous assessment of the scalability of model counters in the wild. To this end, we surveyed 11 application domains and collected an aggregate of 2262 benchmarks from these domains. We then evaluated six state-of-the-art model counters on these instances to assess scalability and runtime performance. Our empirical evaluation demonstrates that the performance of model counters varies significantly across different application domains, underscoring the need for careful selection by the end user. Additionally, we investigated the behavior of different counters with respect to two parameters suggested by the model counting community, finding only a weak correlation. Our analysis highlights the challenges and opportunities for portfolio-based approaches in model counting.

The Cardinality of Identifying Code Sets for Soccer Ball Graph with Application to Remote Sensing

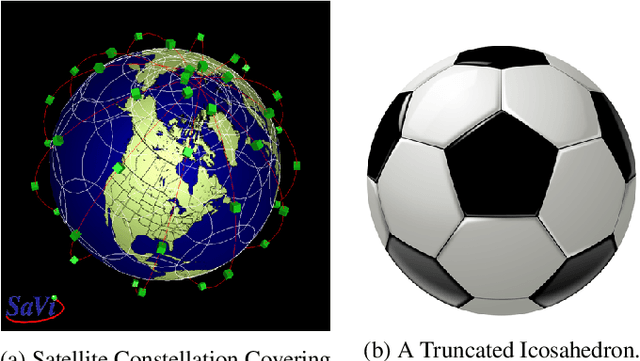
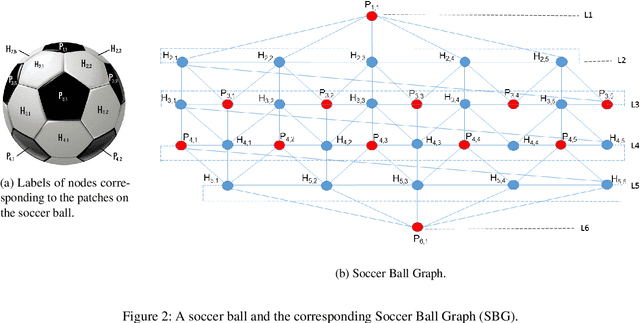
In the context of satellite monitoring of the earth, we can assume that the surface of the earth is divided into a set of regions. We assume that the impact of a big social/environmental event spills into neighboring regions. Using Identifying Code Sets (ICSes), we can deploy sensors in such a way that the region in which an event takes place can be uniquely identified, even with fewer sensors than regions. As Earth is almost a sphere, we use a soccer ball as a model. We construct a Soccer Ball Graph (SBG), and provide human-oriented, analytical proofs that 1) the SBG has at least 26 ICSes of cardinality ten, implying that there are at least 26 different ways to deploy ten satellites to monitor the Earth and 2) that the cardinality of the minimum Identifying Code Set (MICS) for the SBG is at least nine. We then provide a machine-oriented formal proof that the cardinality of the MICS for the SBG is in fact ten, meaning that one must deploy at least ten satellites to monitor the Earth in the SBG model. We also provide machine-oriented proof that there are exactly 26 ICSes of cardinality ten for the SBG.

Formally Certified Approximate Model Counting

Approximate model counting is the task of approximating the number of solutions to an input Boolean formula. The state-of-the-art approximate model counter for formulas in conjunctive normal form (CNF), ApproxMC, provides a scalable means of obtaining model counts with probably approximately correct (PAC)-style guarantees. Nevertheless, the validity of ApproxMC's approximation relies on a careful theoretical analysis of its randomized algorithm and the correctness of its highly optimized implementation, especially the latter's stateful interactions with an incremental CNF satisfiability solver capable of natively handling parity (XOR) constraints. We present the first certification framework for approximate model counting with formally verified guarantees on the quality of its output approximation. Our approach combines: (i) a static, once-off, formal proof of the algorithm's PAC guarantee in the Isabelle/HOL proof assistant; and (ii) dynamic, per-run, verification of ApproxMC's calls to an external CNF-XOR solver using proof certificates. We detail our general approach to establish a rigorous connection between these two parts of the verification, including our blueprint for turning the formalized, randomized algorithm into a verified proof checker, and our design of proof certificates for both ApproxMC and its internal CNF-XOR solving steps. Experimentally, we show that certificate generation adds little overhead to an approximate counter implementation, and that our certificate checker is able to fully certify $84.7\%$ of instances with generated certificates when given the same time and memory limits as the counter.

Locally-Minimal Probabilistic Explanations

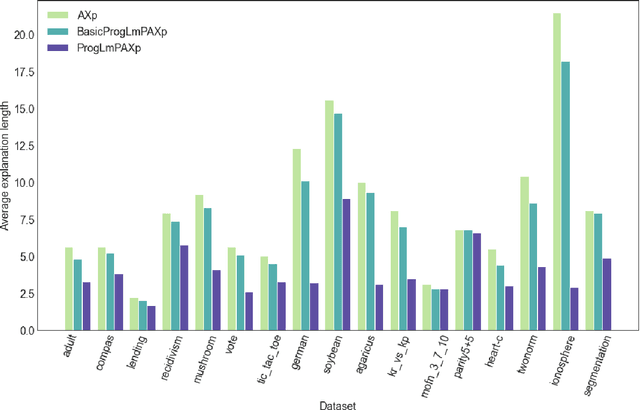
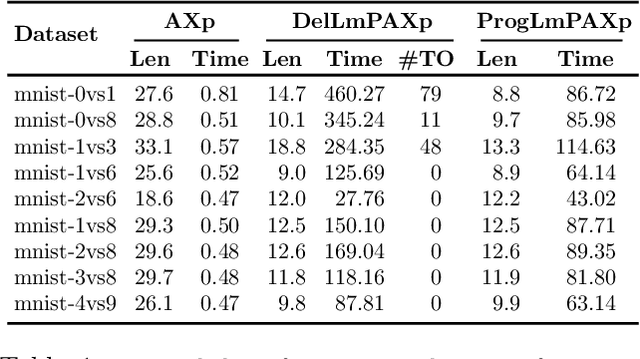
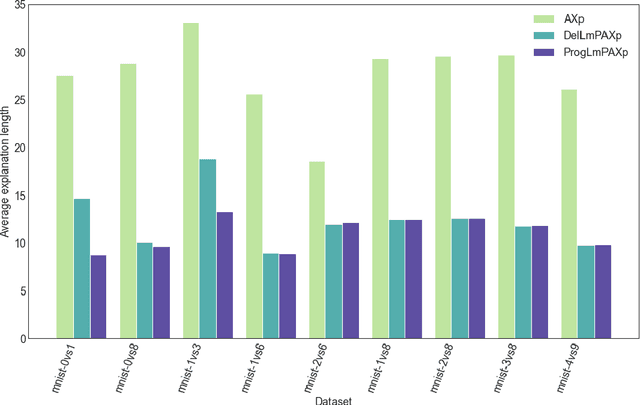
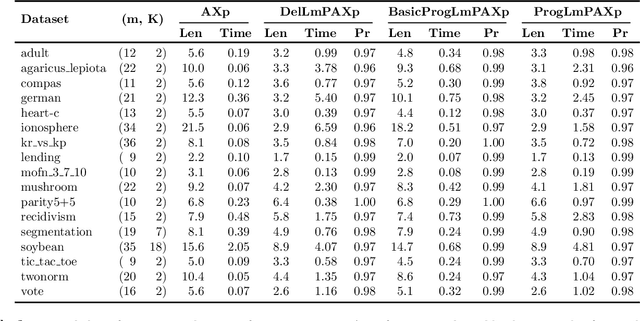
Formal abductive explanations offer crucial guarantees of rigor and so are of interest in high-stakes uses of machine learning (ML). One drawback of abductive explanations is explanation size, justified by the cognitive limits of human decision-makers. Probabilistic abductive explanations (PAXps) address this limitation, but their theoretical and practical complexity makes their exact computation most often unrealistic. This paper proposes novel efficient algorithms for the computation of locally-minimal PXAps, which offer high-quality approximations of PXAps in practice. The experimental results demonstrate the practical efficiency of the proposed algorithms.

Engineering an Exact Pseudo-Boolean Model Counter

Model counting, a fundamental task in computer science, involves determining the number of satisfying assignments to a Boolean formula, typically represented in conjunctive normal form (CNF). While model counting for CNF formulas has received extensive attention with a broad range of applications, the study of model counting for Pseudo-Boolean (PB) formulas has been relatively overlooked. Pseudo-Boolean formulas, being more succinct than propositional Boolean formulas, offer greater flexibility in representing real-world problems. Consequently, there is a crucial need to investigate efficient techniques for model counting for PB formulas. In this work, we propose the first exact Pseudo-Boolean model counter, PBCount, that relies on knowledge compilation approach via algebraic decision diagrams. Our extensive empirical evaluation shows that PBCount can compute counts for 1513 instances while the current state-of-the-art approach could only handle 1013 instances. Our work opens up several avenues for future work in the context of model counting for PB formulas, such as the development of preprocessing techniques and exploration of approaches other than knowledge compilation.

Auditable Algorithms for Approximate Model Counting

Model counting, or counting the satisfying assignments of a Boolean formula, is a fundamental problem with diverse applications. Given #P-hardness of the problem, developing algorithms for approximate counting is an important research area. Building on the practical success of SAT-solvers, the focus has recently shifted from theory to practical implementations of approximate counting algorithms. This has brought to focus new challenges, such as the design of auditable approximate counters that not only provide an approximation of the model count, but also a certificate that a verifier with limited computational power can use to check if the count is indeed within the promised bounds of approximation. Towards generating certificates, we start by examining the best-known deterministic approximate counting algorithm that uses polynomially many calls to a $\Sigma_2^P$ oracle. We show that this can be audited via a $\Sigma_2^P$ oracle with the query constructed over $n^2 \log^2 n$ variables, where the original formula has $n$ variables. Since $n$ is often large, we ask if the count of variables in the certificate can be reduced -- a crucial question for potential implementation. We show that this is indeed possible with a tradeoff in the counting algorithm's complexity. Specifically, we develop new deterministic approximate counting algorithms that invoke a $\Sigma_3^P$ oracle, but can be certified using a $\Sigma_2^P$ oracle using certificates on far fewer variables: our final algorithm uses only $n \log n$ variables. Our study demonstrates that one can simplify auditing significantly if we allow the counting algorithm to access a slightly more powerful oracle. This shows for the first time how audit complexity can be traded for complexity of approximate counting.

Total Variation Distance Estimation Is as Easy as Probabilistic Inference

In this paper, we establish a novel connection between total variation (TV) distance estimation and probabilistic inference. In particular, we present an efficient, structure-preserving reduction from relative approximation of TV distance to probabilistic inference over directed graphical models. This reduction leads to a fully polynomial randomized approximation scheme (FPRAS) for estimating TV distances between distributions over any class of Bayes nets for which there is an efficient probabilistic inference algorithm. In particular, it leads to an FPRAS for estimating TV distances between distributions that are defined by Bayes nets of bounded treewidth. Prior to this work, such approximation schemes only existed for estimating TV distances between product distributions. Our approach employs a new notion of $partial$ couplings of high-dimensional distributions, which might be of independent interest.

Scalable Probabilistic Routes

Inference and prediction of routes have become of interest over the past decade owing to a dramatic increase in package delivery and ride-sharing services. Given the underlying combinatorial structure and the incorporation of probabilities, route prediction involves techniques from both formal methods and machine learning. One promising approach for predicting routes uses decision diagrams that are augmented with probability values. However, the effectiveness of this approach depends on the size of the compiled decision diagrams. The scalability of the approach is limited owing to its empirical runtime and space complexity. In this work, our contributions are two-fold: first, we introduce a relaxed encoding that uses a linear number of variables with respect to the number of vertices in a road network graph to significantly reduce the size of resultant decision diagrams. Secondly, instead of a stepwise sampling procedure, we propose a single pass sampling-based route prediction. In our evaluations arising from a real-world road network, we demonstrate that the resulting system achieves around twice the quality of suggested routes while being an order of magnitude faster compared to state-of-the-art.

Explaining SAT Solving Using Causal Reasoning

The past three decades have witnessed notable success in designing efficient SAT solvers, with modern solvers capable of solving industrial benchmarks containing millions of variables in just a few seconds. The success of modern SAT solvers owes to the widely-used CDCL algorithm, which lacks comprehensive theoretical investigation. Furthermore, it has been observed that CDCL solvers still struggle to deal with specific classes of benchmarks comprising only hundreds of variables, which contrasts with their widespread use in real-world applications. Consequently, there is an urgent need to uncover the inner workings of these seemingly weak yet powerful black boxes. In this paper, we present a first step towards this goal by introducing an approach called CausalSAT, which employs causal reasoning to gain insights into the functioning of modern SAT solvers. CausalSAT initially generates observational data from the execution of SAT solvers and learns a structured graph representing the causal relationships between the components of a SAT solver. Subsequently, given a query such as whether a clause with low literals blocks distance (LBD) has a higher clause utility, CausalSAT calculates the causal effect of LBD on clause utility and provides an answer to the question. We use CausalSAT to quantitatively verify hypotheses previously regarded as "rules of thumb" or empirical findings such as the query above. Moreover, CausalSAT can address previously unexplored questions, like which branching heuristic leads to greater clause utility in order to study the relationship between branching and clause management. Experimental evaluations using practical benchmarks demonstrate that CausalSAT effectively fits the data, verifies four "rules of thumb", and provides answers to three questions closely related to implementing modern solvers.

Rounding Meets Approximate Model Counting

The problem of model counting, also known as #SAT, is to compute the number of models or satisfying assignments of a given Boolean formula $F$. Model counting is a fundamental problem in computer science with a wide range of applications. In recent years, there has been a growing interest in using hashing-based techniques for approximate model counting that provide $(\varepsilon, \delta)$-guarantees: i.e., the count returned is within a $(1+\varepsilon)$-factor of the exact count with confidence at least $1-\delta$. While hashing-based techniques attain reasonable scalability for large enough values of $\delta$, their scalability is severely impacted for smaller values of $\delta$, thereby preventing their adoption in application domains that require estimates with high confidence. The primary contribution of this paper is to address the Achilles heel of hashing-based techniques: we propose a novel approach based on rounding that allows us to achieve a significant reduction in runtime for smaller values of $\delta$. The resulting counter, called RoundMC, achieves a substantial runtime performance improvement over the current state-of-the-art counter, ApproxMC. In particular, our extensive evaluation over a benchmark suite consisting of 1890 instances shows that RoundMC solves 204 more instances than ApproxMC, and achieves a $4\times$ speedup over ApproxMC.