Efficient Sample-optimal Learning of Gaussian Tree Models via Sample-optimal Testing of Gaussian Mutual Information

Learning high-dimensional distributions is a significant challenge in machine learning and statistics. Classical research has mostly concentrated on asymptotic analysis of such data under suitable assumptions. While existing works [Bhattacharyya et al.: SICOMP 2023, Daskalakis et al.: STOC 2021, Choo et al.: ALT 2024] focus on discrete distributions, the current work addresses the tree structure learning problem for Gaussian distributions, providing efficient algorithms with solid theoretical guarantees. This is crucial as real-world distributions are often continuous and differ from the discrete scenarios studied in prior works. In this work, we design a conditional mutual information tester for Gaussian random variables that can test whether two Gaussian random variables are independent, or their conditional mutual information is at least $\varepsilon$, for some parameter $\varepsilon \in (0,1)$ using $\mathcal{O}(\varepsilon^{-1})$ samples which we show to be near-optimal. In contrast, an additive estimation would require $\Omega(\varepsilon^{-2})$ samples. Our upper bound technique uses linear regression on a pair of suitably transformed random variables. Importantly, we show that the chain rule of conditional mutual information continues to hold for the estimated (conditional) mutual information. As an application of such a mutual information tester, we give an efficient $\varepsilon$-approximate structure-learning algorithm for an $n$-variate Gaussian tree model that takes $\widetilde{\Theta}(n\varepsilon^{-1})$ samples which we again show to be near-optimal. In contrast, when the underlying Gaussian model is not known to be tree-structured, we show that $\widetilde{{{\Theta}}}(n^2\varepsilon^{-2})$ samples are necessary and sufficient to output an $\varepsilon$-approximate tree structure. We perform extensive experiments that corroborate our theoretical convergence bounds.

Learnability of Parameter-Bounded Bayes Nets

Bayes nets are extensively used in practice to efficiently represent joint probability distributions over a set of random variables and capture dependency relations. In a seminal paper, Chickering et al. (JMLR 2004) showed that given a distribution $P$, that is defined as the marginal distribution of a Bayes net, it is $\mathsf{NP}$-hard to decide whether there is a parameter-bounded Bayes net that represents $P$. They called this problem LEARN. In this work, we extend the $\mathsf{NP}$-hardness result of LEARN and prove the $\mathsf{NP}$-hardness of a promise search variant of LEARN, whereby the Bayes net in question is guaranteed to exist and one is asked to find such a Bayes net. We complement our hardness result with a positive result about the sample complexity that is sufficient to recover a parameter-bounded Bayes net that is close (in TV distance) to a given distribution $P$, that is represented by some parameter-bounded Bayes net, generalizing a degree-bounded sample complexity result of Brustle et al. (EC 2020).

Distribution Learning Meets Graph Structure Sampling

This work establishes a novel link between the problem of PAC-learning high-dimensional graphical models and the task of (efficient) counting and sampling of graph structures, using an online learning framework. We observe that if we apply the exponentially weighted average (EWA) or randomized weighted majority (RWM) forecasters on a sequence of samples from a distribution P using the log loss function, the average regret incurred by the forecaster's predictions can be used to bound the expected KL divergence between P and the predictions. Known regret bounds for EWA and RWM then yield new sample complexity bounds for learning Bayes nets. Moreover, these algorithms can be made computationally efficient for several interesting classes of Bayes nets. Specifically, we give a new sample-optimal and polynomial time learning algorithm with respect to trees of unknown structure and the first polynomial sample and time algorithm for learning with respect to Bayes nets over a given chordal skeleton.

Total Variation Distance Estimation Is as Easy as Probabilistic Inference

In this paper, we establish a novel connection between total variation (TV) distance estimation and probabilistic inference. In particular, we present an efficient, structure-preserving reduction from relative approximation of TV distance to probabilistic inference over directed graphical models. This reduction leads to a fully polynomial randomized approximation scheme (FPRAS) for estimating TV distances between distributions over any class of Bayes nets for which there is an efficient probabilistic inference algorithm. In particular, it leads to an FPRAS for estimating TV distances between distributions that are defined by Bayes nets of bounded treewidth. Prior to this work, such approximation schemes only existed for estimating TV distances between product distributions. Our approach employs a new notion of $partial$ couplings of high-dimensional distributions, which might be of independent interest.

Efficient inference of interventional distributions

We consider the problem of efficiently inferring interventional distributions in a causal Bayesian network from a finite number of observations. Let $\mathcal{P}$ be a causal model on a set $\mathbf{V}$ of observable variables on a given causal graph $G$. For sets $\mathbf{X},\mathbf{Y}\subseteq \mathbf{V}$, and setting ${\bf x}$ to $\mathbf{X}$, let $P_{\bf x}(\mathbf{Y})$ denote the interventional distribution on $\mathbf{Y}$ with respect to an intervention ${\bf x}$ to variables ${\bf x}$. Shpitser and Pearl (AAAI 2006), building on the work of Tian and Pearl (AAAI 2001), gave an exact characterization of the class of causal graphs for which the interventional distribution $P_{\bf x}({\mathbf{Y}})$ can be uniquely determined. We give the first efficient version of the Shpitser-Pearl algorithm. In particular, under natural assumptions, we give a polynomial-time algorithm that on input a causal graph $G$ on observable variables $\mathbf{V}$, a setting ${\bf x}$ of a set $\mathbf{X} \subseteq \mathbf{V}$ of bounded size, outputs succinct descriptions of both an evaluator and a generator for a distribution $\hat{P}$ that is $\varepsilon$-close (in total variation distance) to $P_{\bf x}({\mathbf{Y}})$ where $Y=\mathbf{V}\setminus \mathbf{X}$, if $P_{\bf x}(\mathbf{Y})$ is identifiable. We also show that when $\mathbf{Y}$ is an arbitrary set, there is no efficient algorithm that outputs an evaluator of a distribution that is $\varepsilon$-close to $P_{\bf x}({\mathbf{Y}})$ unless all problems that have statistical zero-knowledge proofs, including the Graph Isomorphism problem, have efficient randomized algorithms.

Learning Sparse Fixed-Structure Gaussian Bayesian Networks

Gaussian Bayesian networks (a.k.a. linear Gaussian structural equation models) are widely used to model causal interactions among continuous variables. In this work, we study the problem of learning a fixed-structure Gaussian Bayesian network up to a bounded error in total variation distance. We analyze the commonly used node-wise least squares regression (LeastSquares) and prove that it has a near-optimal sample complexity. We also study a couple of new algorithms for the problem: - BatchAvgLeastSquares takes the average of several batches of least squares solutions at each node, so that one can interpolate between the batch size and the number of batches. We show that BatchAvgLeastSquares also has near-optimal sample complexity. - CauchyEst takes the median of solutions to several batches of linear systems at each node. We show that the algorithm specialized to polytrees, CauchyEstTree, has near-optimal sample complexity. Experimentally, we show that for uncontaminated, realizable data, the LeastSquares algorithm performs best, but in the presence of contamination or DAG misspecification, CauchyEst/CauchyEstTree and BatchAvgLeastSquares respectively perform better.

Testing Product Distributions: A Closer Look

We study the problems of identity and closeness testing of $n$-dimensional product distributions. Prior works by Canonne, Diakonikolas, Kane and Stewart (COLT 2017) and Daskalakis and Pan (COLT 2017) have established tight sample complexity bounds for non-tolerant testing over a binary alphabet: given two product distributions $P$ and $Q$ over a binary alphabet, distinguish between the cases $P = Q$ and $d_{\mathrm{TV}}(P, Q) > \epsilon$. We build on this prior work to give a more comprehensive map of the complexity of testing of product distributions by investigating tolerant testing with respect to several natural distance measures and over an arbitrary alphabet. Our study gives a fine-grained understanding of how the sample complexity of tolerant testing varies with the distance measures for product distributions. In addition, we also extend one of our upper bounds on product distributions to bounded-degree Bayes nets.

Near-Optimal Learning of Tree-Structured Distributions by Chow-Liu

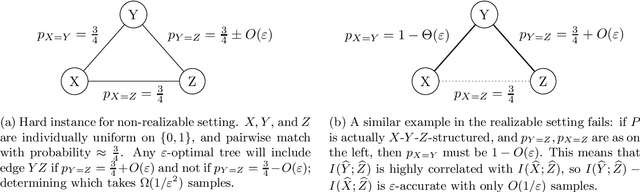
We provide finite sample guarantees for the classical Chow-Liu algorithm (IEEE Trans.~Inform.~Theory, 1968) to learn a tree-structured graphical model of a distribution. For a distribution $P$ on $\Sigma^n$ and a tree $T$ on $n$ nodes, we say $T$ is an $\varepsilon$-approximate tree for $P$ if there is a $T$-structured distribution $Q$ such that $D(P\;||\;Q)$ is at most $\varepsilon$ more than the best possible tree-structured distribution for $P$. We show that if $P$ itself is tree-structured, then the Chow-Liu algorithm with the plug-in estimator for mutual information with $\widetilde{O}(|\Sigma|^3 n\varepsilon^{-1})$ i.i.d.~samples outputs an $\varepsilon$-approximate tree for $P$ with constant probability. In contrast, for a general $P$ (which may not be tree-structured), $\Omega(n^2\varepsilon^{-2})$ samples are necessary to find an $\varepsilon$-approximate tree. Our upper bound is based on a new conditional independence tester that addresses an open problem posed by Canonne, Diakonikolas, Kane, and Stewart~(STOC, 2018): we prove that for three random variables $X,Y,Z$ each over $\Sigma$, testing if $I(X; Y \mid Z)$ is $0$ or $\geq \varepsilon$ is possible with $\widetilde{O}(|\Sigma|^3/\varepsilon)$ samples. Finally, we show that for a specific tree $T$, with $\widetilde{O} (|\Sigma|^2n\varepsilon^{-1})$ samples from a distribution $P$ over $\Sigma^n$, one can efficiently learn the closest $T$-structured distribution in KL divergence by applying the add-1 estimator at each node.

Efficient Distance Approximation for Structured High-Dimensional Distributions via Learning

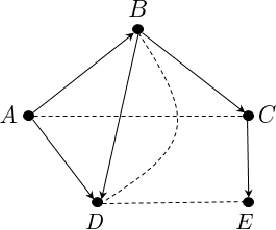
We design efficient distance approximation algorithms for several classes of structured high-dimensional distributions. Specifically, we show algorithms for the following problems: - Given sample access to two Bayesian networks $P_1$ and $P_2$ over known directed acyclic graphs $G_1$ and $G_2$ having $n$ nodes and bounded in-degree, approximate $d_{tv}(P_1,P_2)$ to within additive error $\epsilon$ using $poly(n,\epsilon)$ samples and time - Given sample access to two ferromagnetic Ising models $P_1$ and $P_2$ on $n$ variables with bounded width, approximate $d_{tv}(P_1, P_2)$ to within additive error $\epsilon$ using $poly(n,\epsilon)$ samples and time - Given sample access to two $n$-dimensional Gaussians $P_1$ and $P_2$, approximate $d_{tv}(P_1, P_2)$ to within additive error $\epsilon$ using $poly(n,\epsilon)$ samples and time - Given access to observations from two causal models $P$ and $Q$ on $n$ variables that are defined over known causal graphs, approximate $d_{tv}(P_a, Q_a)$ to within additive error $\epsilon$ using $poly(n,\epsilon)$ samples, where $P_a$ and $Q_a$ are the interventional distributions obtained by the intervention $do(A=a)$ on $P$ and $Q$ respectively for a particular variable $A$. Our results are the first efficient distance approximation algorithms for these well-studied problems. They are derived using a simple and general connection to distribution learning algorithms. The distance approximation algorithms imply new efficient algorithms for {\em tolerant} testing of closeness of the above-mentioned structured high-dimensional distributions.

Efficiently Learning and Sampling Interventional Distributions from Observations

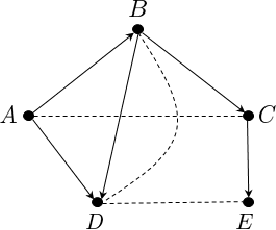
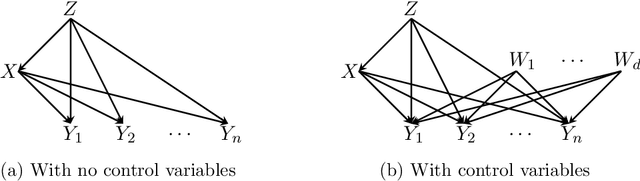
We study the problem of efficiently estimating the effect of an intervention on a single variable using observational samples in a causal Bayesian network. Our goal is to give algorithms that are efficient in both time and sample complexity in a non-parametric setting. Tian and Pearl (AAAI `02) have exactly characterized the class of causal graphs for which causal effects of atomic interventions can be identified from observational data. We make their result quantitative. Suppose P is a causal model on a set V of n observable variables with respect to a given causal graph G with observable distribution $P$. Let $P_x$ denote the interventional distribution over the observables with respect to an intervention of a designated variable X with x. We show that assuming that G has bounded in-degree, bounded c-components, and that the observational distribution is identifiable and satisfies certain strong positivity condition: 1. [Evaluation] There is an algorithm that outputs with probability $2/3$ an evaluator for a distribution $P'$ that satisfies $d_{tv}(P_x, P') \leq \epsilon$ using $m=\tilde{O}(n\epsilon^{-2})$ samples from $P$ and $O(mn)$ time. The evaluator can return in $O(n)$ time the probability $P'(v)$ for any assignment $v$ to $V$. 2. [Generation] There is an algorithm that outputs with probability $2/3$ a sampler for a distribution $\hat{P}$ that satisfies $d_{tv}(P_x, \hat{P}) \leq \epsilon$ using $m=\tilde{O}(n\epsilon^{-2})$ samples from $P$ and $O(mn)$ time. The sampler returns an iid sample from $\hat{P}$ with probability $1-\delta$ in $O(n\epsilon^{-1} \log\delta^{-1})$ time. We extend our techniques to estimate marginals $P_x|_Y$ over a given $Y \subset V$ of interest. We also show lower bounds for the sample complexity showing that our sample complexity has optimal dependence on the parameters n and $\epsilon$ as well as the strong positivity parameter.