The Poisson Midpoint Method for Langevin Dynamics: Provably Efficient Discretization for Diffusion Models

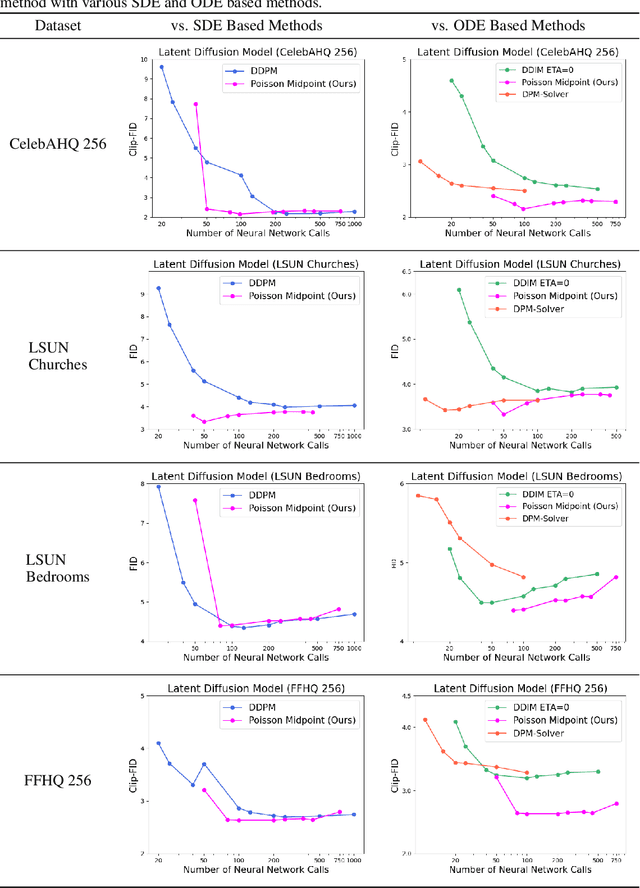
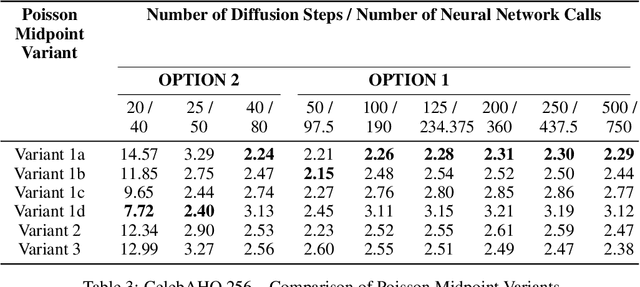
Langevin Dynamics is a Stochastic Differential Equation (SDE) central to sampling and generative modeling and is implemented via time discretization. Langevin Monte Carlo (LMC), based on the Euler-Maruyama discretization, is the simplest and most studied algorithm. LMC can suffer from slow convergence - requiring a large number of steps of small step-size to obtain good quality samples. This becomes stark in the case of diffusion models where a large number of steps gives the best samples, but the quality degrades rapidly with smaller number of steps. Randomized Midpoint Method has been recently proposed as a better discretization of Langevin dynamics for sampling from strongly log-concave distributions. However, important applications such as diffusion models involve non-log concave densities and contain time varying drift. We propose its variant, the Poisson Midpoint Method, which approximates a small step-size LMC with large step-sizes. We prove that this can obtain a quadratic speed up of LMC under very weak assumptions. We apply our method to diffusion models for image generation and show that it maintains the quality of DDPM with 1000 neural network calls with just 50-80 neural network calls and outperforms ODE based methods with similar compute.

Efficient inference of interventional distributions

We consider the problem of efficiently inferring interventional distributions in a causal Bayesian network from a finite number of observations. Let $\mathcal{P}$ be a causal model on a set $\mathbf{V}$ of observable variables on a given causal graph $G$. For sets $\mathbf{X},\mathbf{Y}\subseteq \mathbf{V}$, and setting ${\bf x}$ to $\mathbf{X}$, let $P_{\bf x}(\mathbf{Y})$ denote the interventional distribution on $\mathbf{Y}$ with respect to an intervention ${\bf x}$ to variables ${\bf x}$. Shpitser and Pearl (AAAI 2006), building on the work of Tian and Pearl (AAAI 2001), gave an exact characterization of the class of causal graphs for which the interventional distribution $P_{\bf x}({\mathbf{Y}})$ can be uniquely determined. We give the first efficient version of the Shpitser-Pearl algorithm. In particular, under natural assumptions, we give a polynomial-time algorithm that on input a causal graph $G$ on observable variables $\mathbf{V}$, a setting ${\bf x}$ of a set $\mathbf{X} \subseteq \mathbf{V}$ of bounded size, outputs succinct descriptions of both an evaluator and a generator for a distribution $\hat{P}$ that is $\varepsilon$-close (in total variation distance) to $P_{\bf x}({\mathbf{Y}})$ where $Y=\mathbf{V}\setminus \mathbf{X}$, if $P_{\bf x}(\mathbf{Y})$ is identifiable. We also show that when $\mathbf{Y}$ is an arbitrary set, there is no efficient algorithm that outputs an evaluator of a distribution that is $\varepsilon$-close to $P_{\bf x}({\mathbf{Y}})$ unless all problems that have statistical zero-knowledge proofs, including the Graph Isomorphism problem, have efficient randomized algorithms.

Testing Product Distributions: A Closer Look

We study the problems of identity and closeness testing of $n$-dimensional product distributions. Prior works by Canonne, Diakonikolas, Kane and Stewart (COLT 2017) and Daskalakis and Pan (COLT 2017) have established tight sample complexity bounds for non-tolerant testing over a binary alphabet: given two product distributions $P$ and $Q$ over a binary alphabet, distinguish between the cases $P = Q$ and $d_{\mathrm{TV}}(P, Q) > \epsilon$. We build on this prior work to give a more comprehensive map of the complexity of testing of product distributions by investigating tolerant testing with respect to several natural distance measures and over an arbitrary alphabet. Our study gives a fine-grained understanding of how the sample complexity of tolerant testing varies with the distance measures for product distributions. In addition, we also extend one of our upper bounds on product distributions to bounded-degree Bayes nets.

Efficiently Learning and Sampling Interventional Distributions from Observations

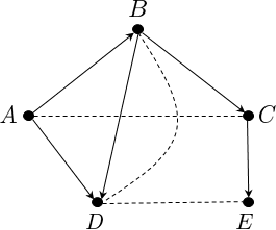
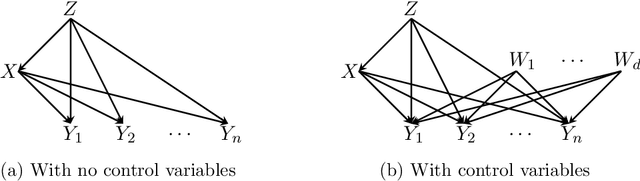
We study the problem of efficiently estimating the effect of an intervention on a single variable using observational samples in a causal Bayesian network. Our goal is to give algorithms that are efficient in both time and sample complexity in a non-parametric setting. Tian and Pearl (AAAI `02) have exactly characterized the class of causal graphs for which causal effects of atomic interventions can be identified from observational data. We make their result quantitative. Suppose P is a causal model on a set V of n observable variables with respect to a given causal graph G with observable distribution $P$. Let $P_x$ denote the interventional distribution over the observables with respect to an intervention of a designated variable X with x. We show that assuming that G has bounded in-degree, bounded c-components, and that the observational distribution is identifiable and satisfies certain strong positivity condition: 1. [Evaluation] There is an algorithm that outputs with probability $2/3$ an evaluator for a distribution $P'$ that satisfies $d_{tv}(P_x, P') \leq \epsilon$ using $m=\tilde{O}(n\epsilon^{-2})$ samples from $P$ and $O(mn)$ time. The evaluator can return in $O(n)$ time the probability $P'(v)$ for any assignment $v$ to $V$. 2. [Generation] There is an algorithm that outputs with probability $2/3$ a sampler for a distribution $\hat{P}$ that satisfies $d_{tv}(P_x, \hat{P}) \leq \epsilon$ using $m=\tilde{O}(n\epsilon^{-2})$ samples from $P$ and $O(mn)$ time. The sampler returns an iid sample from $\hat{P}$ with probability $1-\delta$ in $O(n\epsilon^{-1} \log\delta^{-1})$ time. We extend our techniques to estimate marginals $P_x|_Y$ over a given $Y \subset V$ of interest. We also show lower bounds for the sample complexity showing that our sample complexity has optimal dependence on the parameters n and $\epsilon$ as well as the strong positivity parameter.

Learning and Testing Causal Models with Interventions

We consider testing and learning problems on causal Bayesian networks as defined by Pearl (Pearl, 2009). Given a causal Bayesian network $\mathcal{M}$ on a graph with $n$ discrete variables and bounded in-degree and bounded `confounded components', we show that $O(\log n)$ interventions on an unknown causal Bayesian network $\mathcal{X}$ on the same graph, and $\tilde{O}(n/\epsilon^2)$ samples per intervention, suffice to efficiently distinguish whether $\mathcal{X}=\mathcal{M}$ or whether there exists some intervention under which $\mathcal{X}$ and $\mathcal{M}$ are farther than $\epsilon$ in total variation distance. We also obtain sample/time/intervention efficient algorithms for: (i) testing the identity of two unknown causal Bayesian networks on the same graph; and (ii) learning a causal Bayesian network on a given graph. Although our algorithms are non-adaptive, we show that adaptivity does not help in general: $\Omega(\log n)$ interventions are necessary for testing the identity of two unknown causal Bayesian networks on the same graph, even adaptively. Our algorithms are enabled by a new subadditivity inequality for the squared Hellinger distance between two causal Bayesian networks.