Poisson Midpoint Method for Log Concave Sampling: Beyond the Strong Error Lower Bounds

We study the problem of sampling from strongly log-concave distributions over $\mathbb{R}^d$ using the Poisson midpoint discretization (a variant of the randomized midpoint method) for overdamped/underdamped Langevin dynamics. We prove its convergence in the 2-Wasserstein distance ($W_2$), achieving a cubic speedup in dependence on the target accuracy ($\epsilon$) over the Euler-Maruyama discretization, surpassing existing bounds for randomized midpoint methods. Notably, in the case of underdamped Langevin dynamics, we demonstrate the complexity of $W_2$ convergence is much smaller than the complexity lower bounds for convergence in $L^2$ strong error established in the literature.

Interleaved Gibbs Diffusion for Constrained Generation

We introduce Interleaved Gibbs Diffusion (IGD), a novel generative modeling framework for mixed continuous-discrete data, focusing on constrained generation problems. Prior works on discrete and continuous-discrete diffusion models assume factorized denoising distribution for fast generation, which can hinder the modeling of strong dependencies between random variables encountered in constrained generation. IGD moves beyond this by interleaving continuous and discrete denoising algorithms via a discrete time Gibbs sampling type Markov chain. IGD provides flexibility in the choice of denoisers, allows conditional generation via state-space doubling and inference time scaling via the ReDeNoise method. Empirical evaluations on three challenging tasks-solving 3-SAT, generating molecule structures, and generating layouts-demonstrate state-of-the-art performance. Notably, IGD achieves a 7% improvement on 3-SAT out of the box and achieves state-of-the-art results in molecule generation without relying on equivariant diffusion or domain-specific architectures. We explore a wide range of modeling, and interleaving strategies along with hyperparameters in each of these problems.

Near-Optimal Streaming Heavy-Tailed Statistical Estimation with Clipped SGD

We consider the problem of high-dimensional heavy-tailed statistical estimation in the streaming setting, which is much harder than the traditional batch setting due to memory constraints. We cast this problem as stochastic convex optimization with heavy tailed stochastic gradients, and prove that the widely used Clipped-SGD algorithm attains near-optimal sub-Gaussian statistical rates whenever the second moment of the stochastic gradient noise is finite. More precisely, with $T$ samples, we show that Clipped-SGD, for smooth and strongly convex objectives, achieves an error of $\sqrt{\frac{\mathsf{Tr}(\Sigma)+\sqrt{\mathsf{Tr}(\Sigma)\|\Sigma\|_2}\log(\frac{\log(T)}{\delta})}{T}}$ with probability $1-\delta$, where $\Sigma$ is the covariance of the clipped gradient. Note that the fluctuations (depending on $\frac{1}{\delta}$) are of lower order than the term $\mathsf{Tr}(\Sigma)$. This improves upon the current best rate of $\sqrt{\frac{\mathsf{Tr}(\Sigma)\log(\frac{1}{\delta})}{T}}$ for Clipped-SGD, known only for smooth and strongly convex objectives. Our results also extend to smooth convex and lipschitz convex objectives. Key to our result is a novel iterative refinement strategy for martingale concentration, improving upon the PAC-Bayes approach of Catoni and Giulini.

The Bandit Whisperer: Communication Learning for Restless Bandits

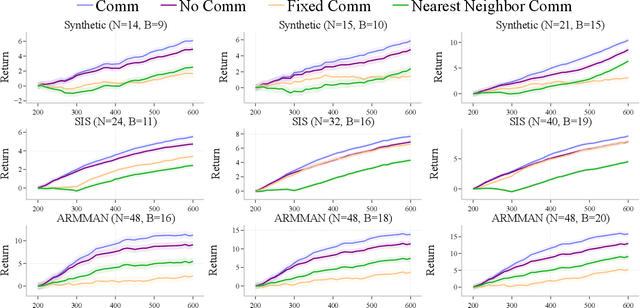
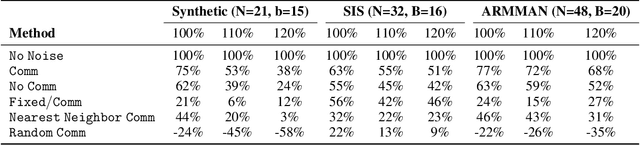
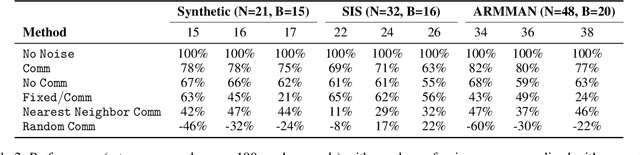
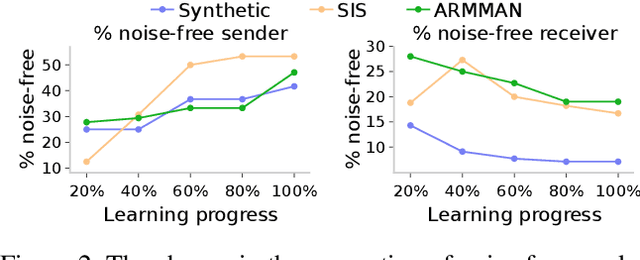
Applying Reinforcement Learning (RL) to Restless Multi-Arm Bandits (RMABs) offers a promising avenue for addressing allocation problems with resource constraints and temporal dynamics. However, classic RMAB models largely overlook the challenges of (systematic) data errors - a common occurrence in real-world scenarios due to factors like varying data collection protocols and intentional noise for differential privacy. We demonstrate that conventional RL algorithms used to train RMABs can struggle to perform well in such settings. To solve this problem, we propose the first communication learning approach in RMABs, where we study which arms, when involved in communication, are most effective in mitigating the influence of such systematic data errors. In our setup, the arms receive Q-function parameters from similar arms as messages to guide behavioral policies, steering Q-function updates. We learn communication strategies by considering the joint utility of messages across all pairs of arms and using a Q-network architecture that decomposes the joint utility. Both theoretical and empirical evidence validate the effectiveness of our method in significantly improving RMAB performance across diverse problems.

Glauber Generative Model: Discrete Diffusion Models via Binary Classification

We introduce the Glauber Generative Model (GGM), a new class of discrete diffusion models, to obtain new samples from a distribution given samples from a discrete space. GGM deploys a discrete Markov chain called the heat bath dynamics (or the Glauber dynamics) to denoise a sequence of noisy tokens to a sample from a joint distribution of discrete tokens. Our novel conceptual framework provides an exact reduction of the task of learning the denoising Markov chain to solving a class of binary classification tasks. More specifically, the model learns to classify a given token in a noisy sequence as signal or noise. In contrast, prior works on discrete diffusion models either solve regression problems to learn importance ratios, or minimize loss functions given by variational approximations. We apply GGM to language modeling and image generation, where images are discretized using image tokenizers like VQGANs. We show that it outperforms existing discrete diffusion models in language generation, and demonstrates strong performance for image generation without using dataset-specific image tokenizers. We also show that our model is capable of performing well in zero-shot control settings like text and image infilling.

The Poisson Midpoint Method for Langevin Dynamics: Provably Efficient Discretization for Diffusion Models

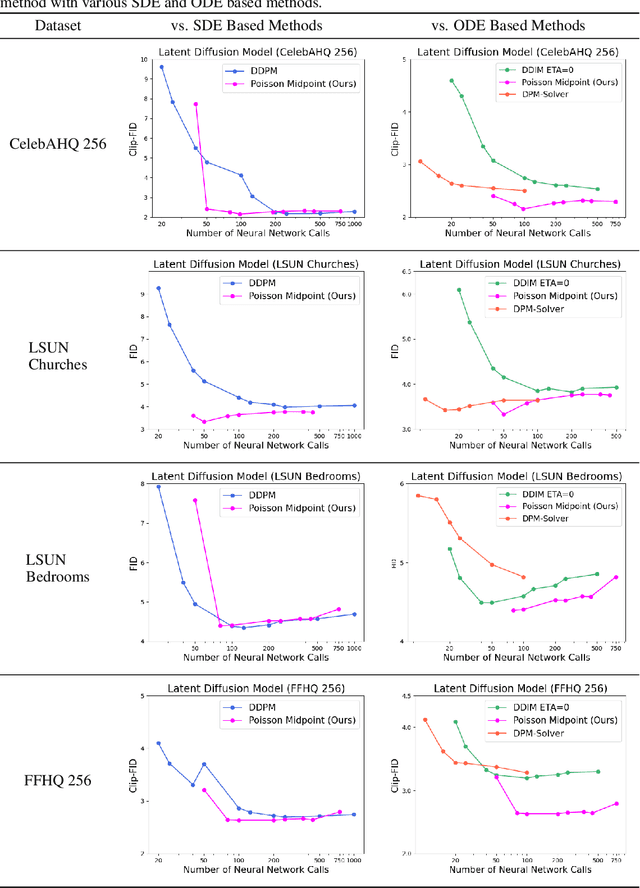
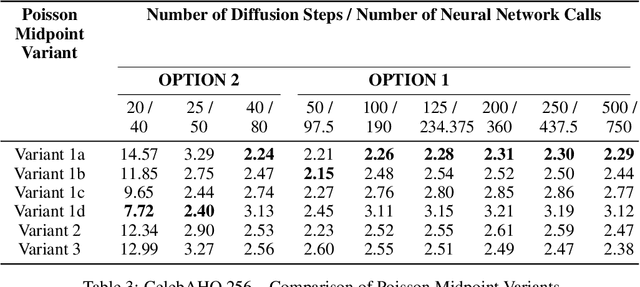
Langevin Dynamics is a Stochastic Differential Equation (SDE) central to sampling and generative modeling and is implemented via time discretization. Langevin Monte Carlo (LMC), based on the Euler-Maruyama discretization, is the simplest and most studied algorithm. LMC can suffer from slow convergence - requiring a large number of steps of small step-size to obtain good quality samples. This becomes stark in the case of diffusion models where a large number of steps gives the best samples, but the quality degrades rapidly with smaller number of steps. Randomized Midpoint Method has been recently proposed as a better discretization of Langevin dynamics for sampling from strongly log-concave distributions. However, important applications such as diffusion models involve non-log concave densities and contain time varying drift. We propose its variant, the Poisson Midpoint Method, which approximates a small step-size LMC with large step-sizes. We prove that this can obtain a quadratic speed up of LMC under very weak assumptions. We apply our method to diffusion models for image generation and show that it maintains the quality of DDPM with 1000 neural network calls with just 50-80 neural network calls and outperforms ODE based methods with similar compute.

A Decision-Language Model (DLM) for Dynamic Restless Multi-Armed Bandit Tasks in Public Health

Efforts to reduce maternal mortality rate, a key UN Sustainable Development target (SDG Target 3.1), rely largely on preventative care programs to spread critical health information to high-risk populations. These programs face two important challenges: efficiently allocating limited health resources to large beneficiary populations, and adapting to evolving policy priorities. While prior works in restless multi-armed bandit (RMAB) demonstrated success in public health allocation tasks, they lack flexibility to adapt to evolving policy priorities. Concurrently, Large Language Models (LLMs) have emerged as adept, automated planners in various domains, including robotic control and navigation. In this paper, we propose DLM: a Decision Language Model for RMABs. To enable dynamic fine-tuning of RMAB policies for challenging public health settings using human-language commands, we propose using LLMs as automated planners to (1) interpret human policy preference prompts, (2) propose code reward functions for a multi-agent RL environment for RMABs, and (3) iterate on the generated reward using feedback from RMAB simulations to effectively adapt policy outcomes. In collaboration with ARMMAN, an India-based public health organization promoting preventative care for pregnant mothers, we conduct a simulation study, showing DLM can dynamically shape policy outcomes using only human language commands as input.

Towards Zero Shot Learning in Restless Multi-armed Bandits

Restless multi-arm bandits (RMABs), a class of resource allocation problems with broad application in areas such as healthcare, online advertising, and anti-poaching, have recently been studied from a multi-agent reinforcement learning perspective. Prior RMAB research suffers from several limitations, e.g., it fails to adequately address continuous states, and requires retraining from scratch when arms opt-in and opt-out over time, a common challenge in many real world applications. We address these limitations by developing a neural network-based pre-trained model (PreFeRMAB) that has general zero-shot ability on a wide range of previously unseen RMABs, and which can be fine-tuned on specific instances in a more sample-efficient way than retraining from scratch. Our model also accommodates general multi-action settings and discrete or continuous state spaces. To enable fast generalization, we learn a novel single policy network model that utilizes feature information and employs a training procedure in which arms opt-in and out over time. We derive a new update rule for a crucial $\lambda$-network with theoretical convergence guarantees and empirically demonstrate the advantages of our approach on several challenging, real-world inspired problems.

Near Optimal Heteroscedastic Regression with Symbiotic Learning

We consider the problem of heteroscedastic linear regression, where, given $n$ samples $(\mathbf{x}_i, y_i)$ from $y_i = \langle \mathbf{w}^{*}, \mathbf{x}_i \rangle + \epsilon_i \cdot \langle \mathbf{f}^{*}, \mathbf{x}_i \rangle$ with $\mathbf{x}_i \sim N(0,\mathbf{I})$, $\epsilon_i \sim N(0,1)$, we aim to estimate $\mathbf{w}^{*}$. Beyond classical applications of such models in statistics, econometrics, time series analysis etc., it is also particularly relevant in machine learning when data is collected from multiple sources of varying but apriori unknown quality. Our work shows that we can estimate $\mathbf{w}^{*}$ in squared norm up to an error of $\tilde{O}\left(\|\mathbf{f}^{*}\|^2 \cdot \left(\frac{1}{n} + \left(\frac{d}{n}\right)^2\right)\right)$ and prove a matching lower bound (upto log factors). This represents a substantial improvement upon the previous best known upper bound of $\tilde{O}\left(\|\mathbf{f}^{*}\|^2\cdot \frac{d}{n}\right)$. Our algorithm is an alternating minimization procedure with two key subroutines 1. An adaptation of the classical weighted least squares heuristic to estimate $\mathbf{w}^{*}$, for which we provide the first non-asymptotic guarantee. 2. A nonconvex pseudogradient descent procedure for estimating $\mathbf{f}^{*}$ inspired by phase retrieval. As corollaries, we obtain fast non-asymptotic rates for two important problems, linear regression with multiplicative noise and phase retrieval with multiplicative noise, both of which are of independent interest. Beyond this, the proof of our lower bound, which involves a novel adaptation of LeCam's method for handling infinite mutual information quantities (thereby preventing a direct application of standard techniques like Fano's method), could also be of broader interest for establishing lower bounds for other heteroscedastic or heavy-tailed statistical problems.

Stochastic Re-weighted Gradient Descent via Distributionally Robust Optimization

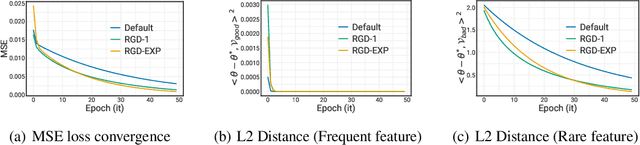
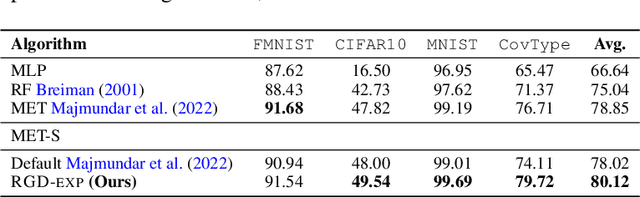
We develop a re-weighted gradient descent technique for boosting the performance of deep neural networks. Our algorithm involves the importance weighting of data points during each optimization step. Our approach is inspired by distributionally robust optimization with $f$-divergences, which has been known to result in models with improved generalization guarantees. Our re-weighting scheme is simple, computationally efficient, and can be combined with any popular optimization algorithms such as SGD and Adam. Empirically, we demonstrate our approach's superiority on various tasks, including vanilla classification, classification with label imbalance, noisy labels, domain adaptation, and tabular representation learning. Notably, we obtain improvements of +0.7% and +1.44% over SOTA on DomainBed and Tabular benchmarks, respectively. Moreover, our algorithm boosts the performance of BERT on GLUE benchmarks by +1.94%, and ViT on ImageNet-1K by +0.9%. These results demonstrate the effectiveness of the proposed approach, indicating its potential for improving performance in diverse domains.