Interleaved Gibbs Diffusion for Constrained Generation

We introduce Interleaved Gibbs Diffusion (IGD), a novel generative modeling framework for mixed continuous-discrete data, focusing on constrained generation problems. Prior works on discrete and continuous-discrete diffusion models assume factorized denoising distribution for fast generation, which can hinder the modeling of strong dependencies between random variables encountered in constrained generation. IGD moves beyond this by interleaving continuous and discrete denoising algorithms via a discrete time Gibbs sampling type Markov chain. IGD provides flexibility in the choice of denoisers, allows conditional generation via state-space doubling and inference time scaling via the ReDeNoise method. Empirical evaluations on three challenging tasks-solving 3-SAT, generating molecule structures, and generating layouts-demonstrate state-of-the-art performance. Notably, IGD achieves a 7% improvement on 3-SAT out of the box and achieves state-of-the-art results in molecule generation without relying on equivariant diffusion or domain-specific architectures. We explore a wide range of modeling, and interleaving strategies along with hyperparameters in each of these problems.

Infinite Width Limits of Self Supervised Neural Networks

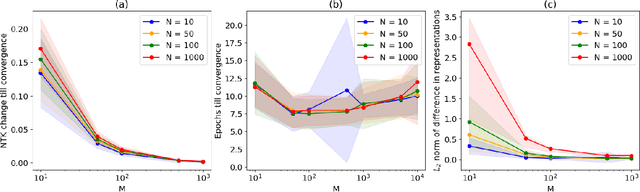
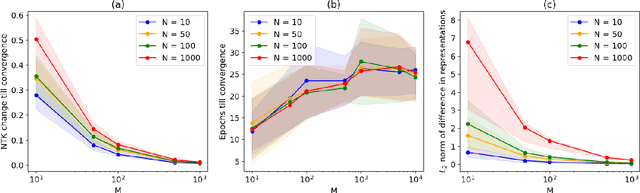
The NTK is a widely used tool in the theoretical analysis of deep learning, allowing us to look at supervised deep neural networks through the lenses of kernel regression. Recently, several works have investigated kernel models for self-supervised learning, hypothesizing that these also shed light on the behaviour of wide neural networks by virtue of the NTK. However, it remains an open question to what extent this connection is mathematically sound -- it is a commonly encountered misbelief that the kernel behaviour of wide neural networks emerges irrespective of the loss function it is trained on. In this paper, we bridge the gap between the NTK and self-supervised learning, focusing on two-layer neural networks trained under the Barlow Twins loss. We prove that the NTK of Barlow Twins indeed becomes constant as the width of the network approaches infinity. Our analysis technique is different from previous works on the NTK and may be of independent interest. Overall, our work provides a first rigorous justification for the use of classic kernel theory to understand self-supervised learning of wide neural networks. Building on this result, we derive generalization error bounds for kernelized Barlow Twins and connect them to neural networks of finite width.

When can we Approximate Wide Contrastive Models with Neural Tangent Kernels and Principal Component Analysis?

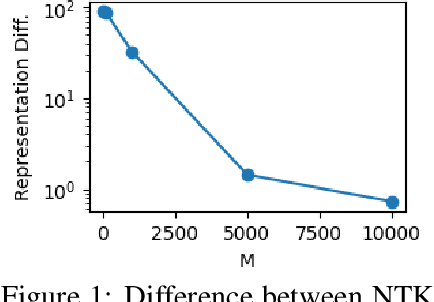
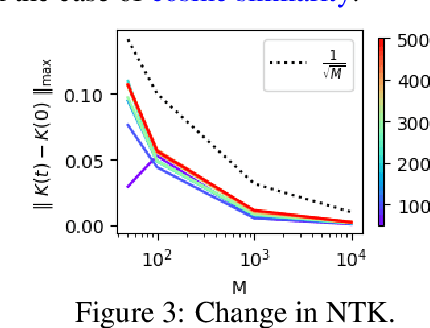
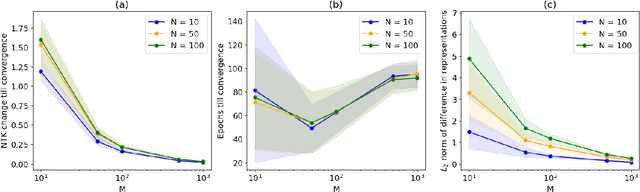
Contrastive learning is a paradigm for learning representations from unlabelled data that has been highly successful for image and text data. Several recent works have examined contrastive losses to claim that contrastive models effectively learn spectral embeddings, while few works show relations between (wide) contrastive models and kernel principal component analysis (PCA). However, it is not known if trained contrastive models indeed correspond to kernel methods or PCA. In this work, we analyze the training dynamics of two-layer contrastive models, with non-linear activation, and answer when these models are close to PCA or kernel methods. It is well known in the supervised setting that neural networks are equivalent to neural tangent kernel (NTK) machines, and that the NTK of infinitely wide networks remains constant during training. We provide the first convergence results of NTK for contrastive losses, and present a nuanced picture: NTK of wide networks remains almost constant for cosine similarity based contrastive losses, but not for losses based on dot product similarity. We further study the training dynamics of contrastive models with orthogonality constraints on output layer, which is implicitly assumed in works relating contrastive learning to spectral embedding. Our deviation bounds suggest that representations learned by contrastive models are close to the principal components of a certain matrix computed from random features. We empirically show that our theoretical results possibly hold beyond two-layer networks.