Cluster Specific Representation Learning

Representation learning aims to extract meaningful lower-dimensional embeddings from data, known as representations. Despite its widespread application, there is no established definition of a ``good'' representation. Typically, the representation quality is evaluated based on its performance in downstream tasks such as clustering, de-noising, etc. However, this task-specific approach has a limitation where a representation that performs well for one task may not necessarily be effective for another. This highlights the need for a more agnostic formulation, which is the focus of our work. We propose a downstream-agnostic formulation: when inherent clusters exist in the data, the representations should be specific to each cluster. Under this idea, we develop a meta-algorithm that jointly learns cluster-specific representations and cluster assignments. As our approach is easy to integrate with any representation learning framework, we demonstrate its effectiveness in various setups, including Autoencoders, Variational Autoencoders, Contrastive learning models, and Restricted Boltzmann Machines. We qualitatively compare our cluster-specific embeddings to standard embeddings and downstream tasks such as de-noising and clustering. While our method slightly increases runtime and parameters compared to the standard model, the experiments clearly show that it extracts the inherent cluster structures in the data, resulting in improved performance in relevant applications.

When can we Approximate Wide Contrastive Models with Neural Tangent Kernels and Principal Component Analysis?

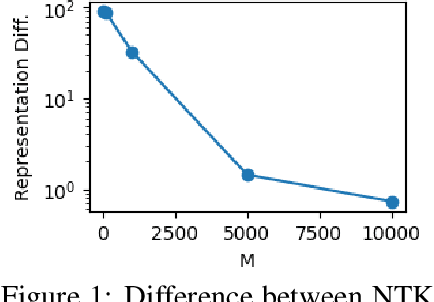
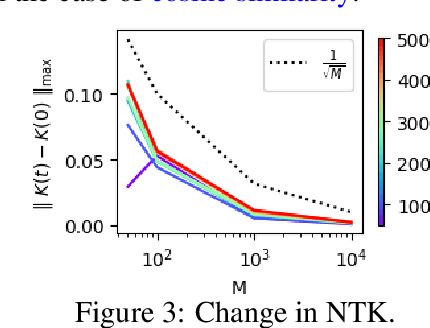
Contrastive learning is a paradigm for learning representations from unlabelled data that has been highly successful for image and text data. Several recent works have examined contrastive losses to claim that contrastive models effectively learn spectral embeddings, while few works show relations between (wide) contrastive models and kernel principal component analysis (PCA). However, it is not known if trained contrastive models indeed correspond to kernel methods or PCA. In this work, we analyze the training dynamics of two-layer contrastive models, with non-linear activation, and answer when these models are close to PCA or kernel methods. It is well known in the supervised setting that neural networks are equivalent to neural tangent kernel (NTK) machines, and that the NTK of infinitely wide networks remains constant during training. We provide the first convergence results of NTK for contrastive losses, and present a nuanced picture: NTK of wide networks remains almost constant for cosine similarity based contrastive losses, but not for losses based on dot product similarity. We further study the training dynamics of contrastive models with orthogonality constraints on output layer, which is implicitly assumed in works relating contrastive learning to spectral embedding. Our deviation bounds suggest that representations learned by contrastive models are close to the principal components of a certain matrix computed from random features. We empirically show that our theoretical results possibly hold beyond two-layer networks.

Non-Parametric Representation Learning with Kernels

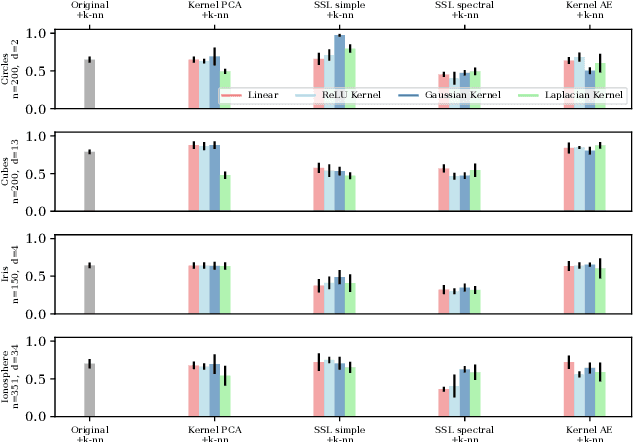
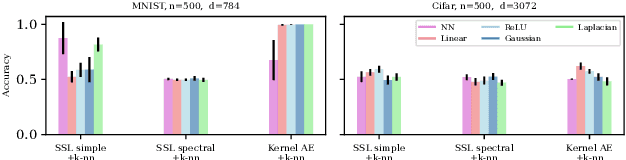
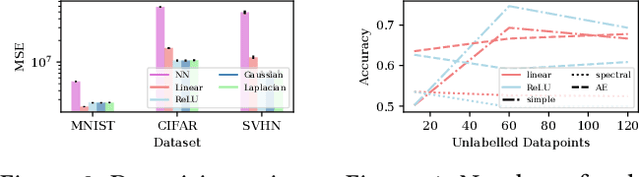
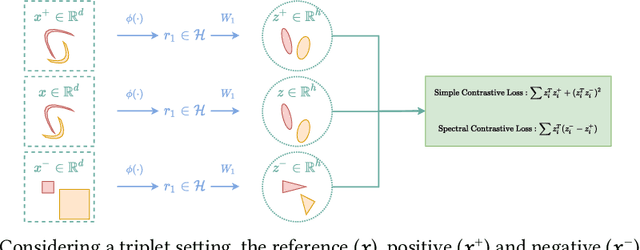
Unsupervised and self-supervised representation learning has become popular in recent years for learning useful features from unlabelled data. Representation learning has been mostly developed in the neural network literature, and other models for representation learning are surprisingly unexplored. In this work, we introduce and analyze several kernel-based representation learning approaches: Firstly, we define two kernel Self-Supervised Learning (SSL) models using contrastive loss functions and secondly, a Kernel Autoencoder (AE) model based on the idea of embedding and reconstructing data. We argue that the classical representer theorems for supervised kernel machines are not always applicable for (self-supervised) representation learning, and present new representer theorems, which show that the representations learned by our kernel models can be expressed in terms of kernel matrices. We further derive generalisation error bounds for representation learning with kernel SSL and AE, and empirically evaluate the performance of these methods in both small data regimes as well as in comparison with neural network based models.

Representation Learning Dynamics of Self-Supervised Models

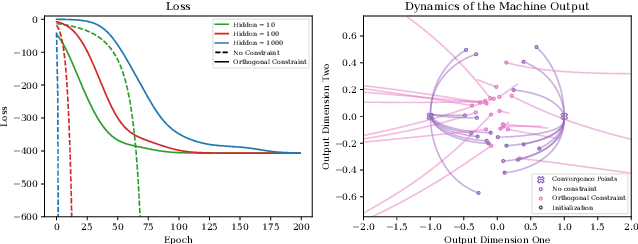
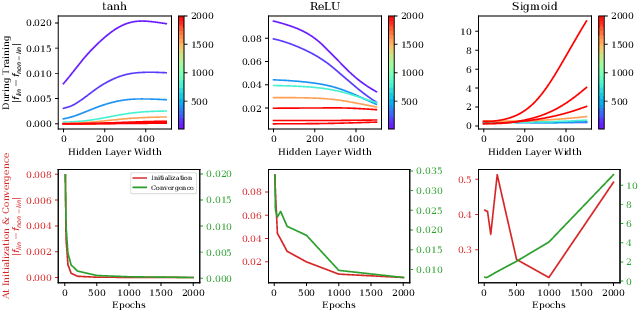
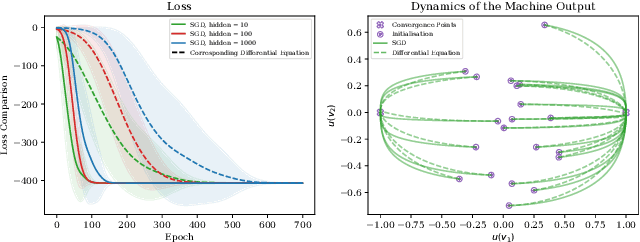
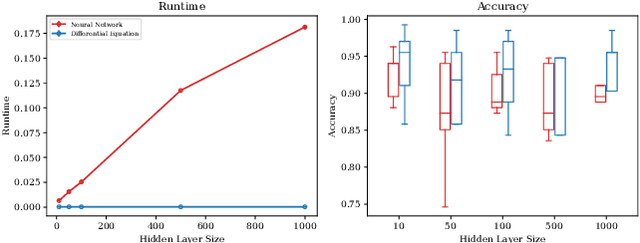
Self-Supervised Learning (SSL) is an important paradigm for learning representations from unlabelled data, and SSL with neural networks has been highly successful in practice. However current theoretical analysis of SSL is mostly restricted to generalisation error bounds. In contrast, learning dynamics often provide a precise characterisation of the behaviour of neural networks based models but, so far, are mainly known in supervised settings. In this paper, we study the learning dynamics of SSL models, specifically representations obtained by minimising contrastive and non-contrastive losses. We show that a naive extension of the dymanics of multivariate regression to SSL leads to learning trivial scalar representations that demonstrates dimension collapse in SSL. Consequently, we formulate SSL objectives with orthogonality constraints on the weights, and derive the exact (network width independent) learning dynamics of the SSL models trained using gradient descent on the Grassmannian manifold. We also argue that the infinite width approximation of SSL models significantly deviate from the neural tangent kernel approximations of supervised models. We numerically illustrate the validity of our theoretical findings, and discuss how the presented results provide a framework for further theoretical analysis of contrastive and non-contrastive SSL.

Representation Power of Graph Convolutions : Neural Tangent Kernel Analysis

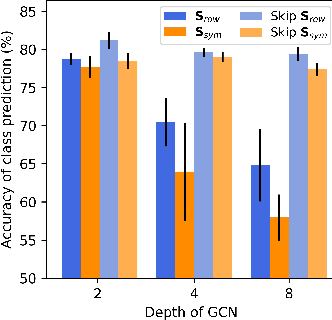
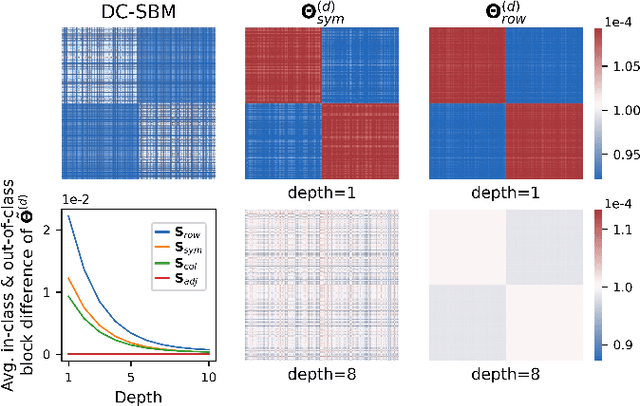
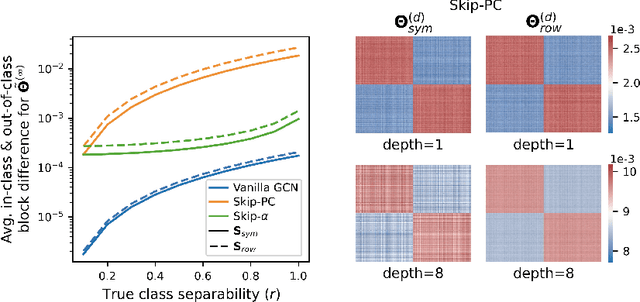
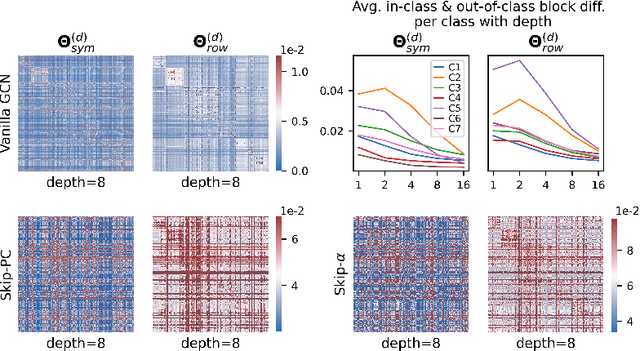
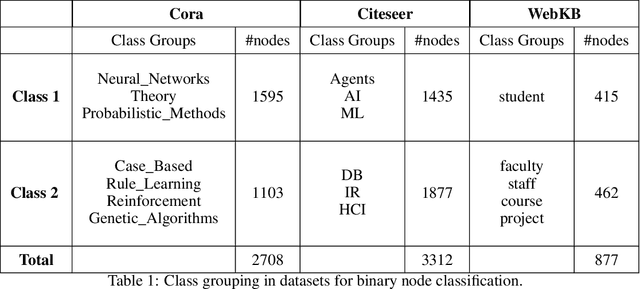
The fundamental principle of Graph Neural Networks (GNNs) is to exploit the structural information of the data by aggregating the neighboring nodes using a graph convolution. Therefore, understanding its influence on the network performance is crucial. Convolutions based on graph Laplacian have emerged as the dominant choice with the symmetric normalization of the adjacency matrix $A$, defined as $D^{-1/2}AD^{-1/2}$, being the most widely adopted one, where $D$ is the degree matrix. However, some empirical studies show that row normalization $D^{-1}A$ outperforms it in node classification. Despite the widespread use of GNNs, there is no rigorous theoretical study on the representation power of these convolution operators, that could explain this behavior. In this work, we analyze the influence of the graph convolutions theoretically using Graph Neural Tangent Kernel in a semi-supervised node classification setting. Under a Degree Corrected Stochastic Block Model, we prove that: (i) row normalization preserves the underlying class structure better than other convolutions; (ii) performance degrades with network depth due to over-smoothing, but the loss in class information is the slowest in row normalization; (iii) skip connections retain the class information even at infinite depth, thereby eliminating over-smoothing. We finally validate our theoretical findings on real datasets.

New Insights into Graph Convolutional Networks using Neural Tangent Kernels

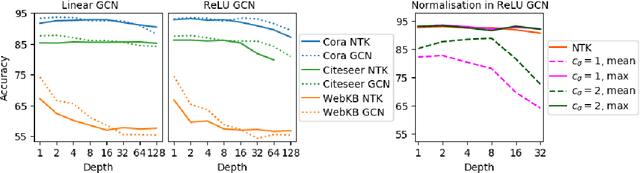
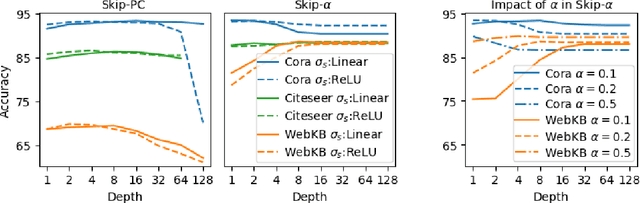
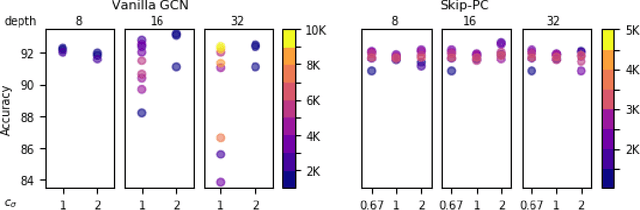
Graph Convolutional Networks (GCNs) have emerged as powerful tools for learning on network structured data. Although empirically successful, GCNs exhibit certain behaviour that has no rigorous explanation -- for instance, the performance of GCNs significantly degrades with increasing network depth, whereas it improves marginally with depth using skip connections. This paper focuses on semi-supervised learning on graphs, and explains the above observations through the lens of Neural Tangent Kernels (NTKs). We derive NTKs corresponding to infinitely wide GCNs (with and without skip connections). Subsequently, we use the derived NTKs to identify that, with suitable normalisation, network depth does not always drastically reduce the performance of GCNs -- a fact that we also validate through extensive simulation. Furthermore, we propose NTK as an efficient `surrogate model' for GCNs that does not suffer from performance fluctuations due to hyper-parameter tuning since it is a hyper-parameter free deterministic kernel. The efficacy of this idea is demonstrated through a comparison of different skip connections for GCNs using the surrogate NTKs.