The Poisson Midpoint Method for Langevin Dynamics: Provably Efficient Discretization for Diffusion Models
Paper and Code
May 27, 2024

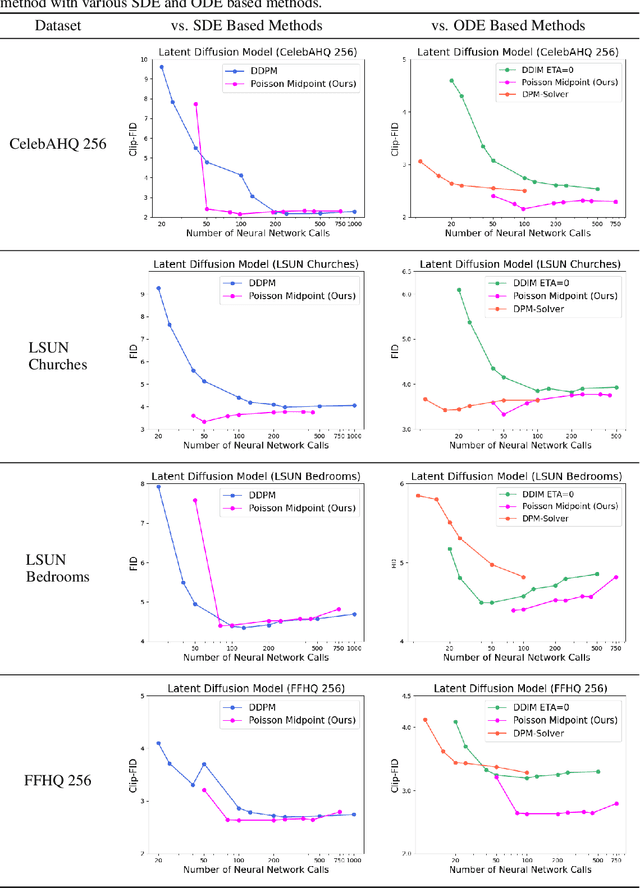
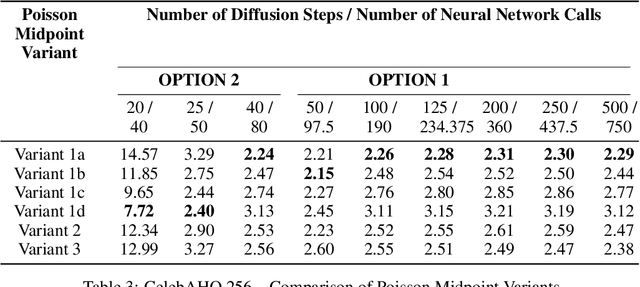
Langevin Dynamics is a Stochastic Differential Equation (SDE) central to sampling and generative modeling and is implemented via time discretization. Langevin Monte Carlo (LMC), based on the Euler-Maruyama discretization, is the simplest and most studied algorithm. LMC can suffer from slow convergence - requiring a large number of steps of small step-size to obtain good quality samples. This becomes stark in the case of diffusion models where a large number of steps gives the best samples, but the quality degrades rapidly with smaller number of steps. Randomized Midpoint Method has been recently proposed as a better discretization of Langevin dynamics for sampling from strongly log-concave distributions. However, important applications such as diffusion models involve non-log concave densities and contain time varying drift. We propose its variant, the Poisson Midpoint Method, which approximates a small step-size LMC with large step-sizes. We prove that this can obtain a quadratic speed up of LMC under very weak assumptions. We apply our method to diffusion models for image generation and show that it maintains the quality of DDPM with 1000 neural network calls with just 50-80 neural network calls and outperforms ODE based methods with similar compute.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge