Diffusion Models are Secretly Exchangeable: Parallelizing DDPMs via Autospeculation

Denoising Diffusion Probabilistic Models (DDPMs) have emerged as powerful tools for generative modeling. However, their sequential computation requirements lead to significant inference-time bottlenecks. In this work, we utilize the connection between DDPMs and Stochastic Localization to prove that, under an appropriate reparametrization, the increments of DDPM satisfy an exchangeability property. This general insight enables near-black-box adaptation of various performance optimization techniques from autoregressive models to the diffusion setting. To demonstrate this, we introduce \emph{Autospeculative Decoding} (ASD), an extension of the widely used speculative decoding algorithm to DDPMs that does not require any auxiliary draft models. Our theoretical analysis shows that ASD achieves a $\tilde{O} (K^{\frac{1}{3}})$ parallel runtime speedup over the $K$ step sequential DDPM. We also demonstrate that a practical implementation of autospeculative decoding accelerates DDPM inference significantly in various domains.

ColonNet: A Hybrid Of DenseNet121 And U-NET Model For Detection And Segmentation Of GI Bleeding

This study presents an integrated deep learning model for automatic detection and classification of Gastrointestinal bleeding in the frames extracted from Wireless Capsule Endoscopy (WCE) videos. The dataset has been released as part of Auto-WCBleedGen Challenge Version V2 hosted by the MISAHUB team. Our model attained the highest performance among 75 teams that took part in this competition. It aims to efficiently utilizes CNN based model i.e. DenseNet and UNet to detect and segment bleeding and non-bleeding areas in the real-world complex dataset. The model achieves an impressive overall accuracy of 80% which would surely help a skilled doctor to carry out further diagnostics.

Near-Optimal Streaming Heavy-Tailed Statistical Estimation with Clipped SGD

We consider the problem of high-dimensional heavy-tailed statistical estimation in the streaming setting, which is much harder than the traditional batch setting due to memory constraints. We cast this problem as stochastic convex optimization with heavy tailed stochastic gradients, and prove that the widely used Clipped-SGD algorithm attains near-optimal sub-Gaussian statistical rates whenever the second moment of the stochastic gradient noise is finite. More precisely, with $T$ samples, we show that Clipped-SGD, for smooth and strongly convex objectives, achieves an error of $\sqrt{\frac{\mathsf{Tr}(\Sigma)+\sqrt{\mathsf{Tr}(\Sigma)\|\Sigma\|_2}\log(\frac{\log(T)}{\delta})}{T}}$ with probability $1-\delta$, where $\Sigma$ is the covariance of the clipped gradient. Note that the fluctuations (depending on $\frac{1}{\delta}$) are of lower order than the term $\mathsf{Tr}(\Sigma)$. This improves upon the current best rate of $\sqrt{\frac{\mathsf{Tr}(\Sigma)\log(\frac{1}{\delta})}{T}}$ for Clipped-SGD, known only for smooth and strongly convex objectives. Our results also extend to smooth convex and lipschitz convex objectives. Key to our result is a novel iterative refinement strategy for martingale concentration, improving upon the PAC-Bayes approach of Catoni and Giulini.

CapsuleNet: A Deep Learning Model To Classify GI Diseases Using EfficientNet-b7

Gastrointestinal (GI) diseases represent a significant global health concern, with Capsule Endoscopy (CE) offering a non-invasive method for diagnosis by capturing a large number of GI tract images. However, the sheer volume of video frames necessitates automated analysis to reduce the workload on doctors and increase the diagnostic accuracy. In this paper, we present CapsuleNet, a deep learning model developed for the Capsule Vision 2024 Challenge, aimed at classifying 10 distinct GI abnormalities. Using a highly imbalanced dataset, we implemented various data augmentation strategies, reducing the data imbalance to a manageable level. Our model leverages a pretrained EfficientNet-b7 backbone, tuned with additional layers for classification and optimized with PReLU activation functions. The model demonstrated superior performance on validation data, achieving a micro accuracy of 84.5% and outperforming the VGG16 baseline across most classes. Despite these advances, challenges remain in classifying certain abnormalities, such as Erythema. Our findings suggest that CNN-based models like CapsuleNet can provide an efficient solution for GI tract disease classification, particularly when inference time is a critical factor.

Near Optimal Heteroscedastic Regression with Symbiotic Learning

We consider the problem of heteroscedastic linear regression, where, given $n$ samples $(\mathbf{x}_i, y_i)$ from $y_i = \langle \mathbf{w}^{*}, \mathbf{x}_i \rangle + \epsilon_i \cdot \langle \mathbf{f}^{*}, \mathbf{x}_i \rangle$ with $\mathbf{x}_i \sim N(0,\mathbf{I})$, $\epsilon_i \sim N(0,1)$, we aim to estimate $\mathbf{w}^{*}$. Beyond classical applications of such models in statistics, econometrics, time series analysis etc., it is also particularly relevant in machine learning when data is collected from multiple sources of varying but apriori unknown quality. Our work shows that we can estimate $\mathbf{w}^{*}$ in squared norm up to an error of $\tilde{O}\left(\|\mathbf{f}^{*}\|^2 \cdot \left(\frac{1}{n} + \left(\frac{d}{n}\right)^2\right)\right)$ and prove a matching lower bound (upto log factors). This represents a substantial improvement upon the previous best known upper bound of $\tilde{O}\left(\|\mathbf{f}^{*}\|^2\cdot \frac{d}{n}\right)$. Our algorithm is an alternating minimization procedure with two key subroutines 1. An adaptation of the classical weighted least squares heuristic to estimate $\mathbf{w}^{*}$, for which we provide the first non-asymptotic guarantee. 2. A nonconvex pseudogradient descent procedure for estimating $\mathbf{f}^{*}$ inspired by phase retrieval. As corollaries, we obtain fast non-asymptotic rates for two important problems, linear regression with multiplicative noise and phase retrieval with multiplicative noise, both of which are of independent interest. Beyond this, the proof of our lower bound, which involves a novel adaptation of LeCam's method for handling infinite mutual information quantities (thereby preventing a direct application of standard techniques like Fano's method), could also be of broader interest for establishing lower bounds for other heteroscedastic or heavy-tailed statistical problems.

Provably Fast Finite Particle Variants of SVGD via Virtual Particle Stochastic Approximation

Stein Variational Gradient Descent (SVGD) is a popular variational inference algorithm which simulates an interacting particle system to approximately sample from a target distribution, with impressive empirical performance across various domains. Theoretically, its population (i.e, infinite-particle) limit dynamics is well studied but the behavior of SVGD in the finite-particle regime is much less understood. In this work, we design two computationally efficient variants of SVGD, namely VP-SVGD (which is conceptually elegant) and GB-SVGD (which is empirically effective), with provably fast finite-particle convergence rates. We introduce the notion of \emph{virtual particles} and develop novel stochastic approximations of population-limit SVGD dynamics in the space of probability measures, which are exactly implementable using a finite number of particles. Our algorithms can be viewed as specific random-batch approximations of SVGD, which are computationally more efficient than ordinary SVGD. We show that the $n$ particles output by VP-SVGD and GB-SVGD, run for $T$ steps with batch-size $K$, are at-least as good as i.i.d samples from a distribution whose Kernel Stein Discrepancy to the target is at most $O\left(\tfrac{d^{1/3}}{(KT)^{1/6}}\right)$ under standard assumptions. Our results also hold under a mild growth condition on the potential function, which is much weaker than the isoperimetric (e.g. Poincare Inequality) or information-transport conditions (e.g. Talagrand's Inequality $\mathsf{T}_1$) generally considered in prior works. As a corollary, we consider the convergence of the empirical measure (of the particles output by VP-SVGD and GB-SVGD) to the target distribution and demonstrate a \emph{double exponential improvement} over the best known finite-particle analysis of SVGD.

Sampling without Replacement Leads to Faster Rates in Finite-Sum Minimax Optimization

We analyze the convergence rates of stochastic gradient algorithms for smooth finite-sum minimax optimization and show that, for many such algorithms, sampling the data points without replacement leads to faster convergence compared to sampling with replacement. For the smooth and strongly convex-strongly concave setting, we consider gradient descent ascent and the proximal point method, and present a unified analysis of two popular without-replacement sampling strategies, namely Random Reshuffling (RR), which shuffles the data every epoch, and Single Shuffling or Shuffle Once (SO), which shuffles only at the beginning. We obtain tight convergence rates for RR and SO and demonstrate that these strategies lead to faster convergence than uniform sampling. Moving beyond convexity, we obtain similar results for smooth nonconvex-nonconcave objectives satisfying a two-sided Polyak-{\L}ojasiewicz inequality. Finally, we demonstrate that our techniques are general enough to analyze the effect of data-ordering attacks, where an adversary manipulates the order in which data points are supplied to the optimizer. Our analysis also recovers tight rates for the incremental gradient method, where the data points are not shuffled at all.

NeurInt : Learning to Interpolate through Neural ODEs

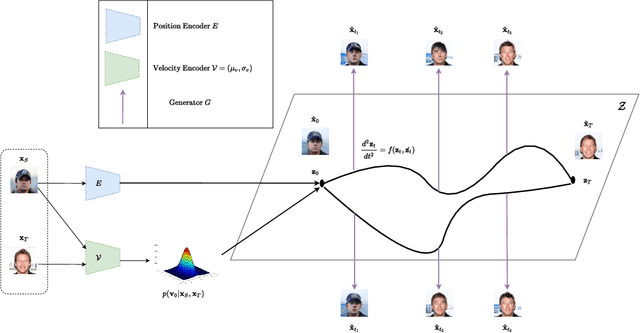
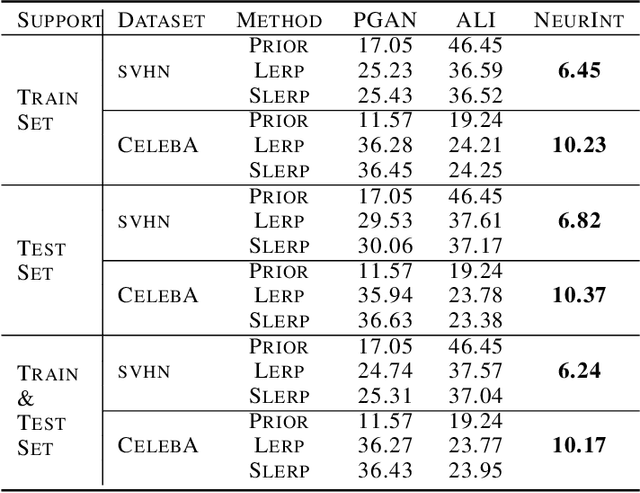
A wide range of applications require learning image generation models whose latent space effectively captures the high-level factors of variation present in the data distribution. The extent to which a model represents such variations through its latent space can be judged by its ability to interpolate between images smoothly. However, most generative models mapping a fixed prior to the generated images lead to interpolation trajectories lacking smoothness and containing images of reduced quality. In this work, we propose a novel generative model that learns a flexible non-parametric prior over interpolation trajectories, conditioned on a pair of source and target images. Instead of relying on deterministic interpolation methods (such as linear or spherical interpolation in latent space), we devise a framework that learns a distribution of trajectories between two given images using Latent Second-Order Neural Ordinary Differential Equations. Through a hybrid combination of reconstruction and adversarial losses, the generator is trained to map the sampled points from these trajectories to sequences of realistic images that smoothly transition from the source to the target image. Through comprehensive qualitative and quantitative experiments, we demonstrate our approach's effectiveness in generating images of improved quality as well as its ability to learn a diverse distribution over smooth interpolation trajectories for any pair of real source and target images.

Jointly Trained Image and Video Generation using Residual Vectors

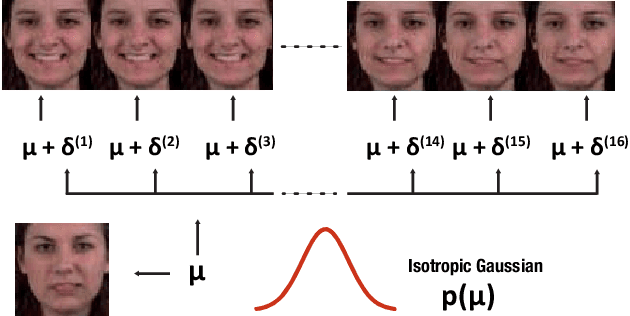
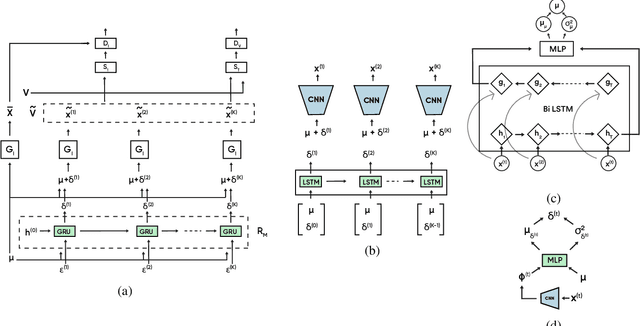
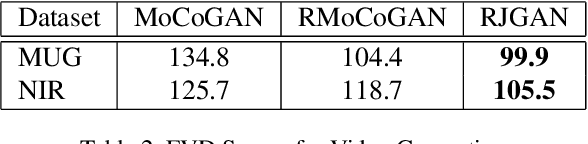
In this work, we propose a modeling technique for jointly training image and video generation models by simultaneously learning to map latent variables with a fixed prior onto real images and interpolate over images to generate videos. The proposed approach models the variations in representations using residual vectors encoding the change at each time step over a summary vector for the entire video. We utilize the technique to jointly train an image generation model with a fixed prior along with a video generation model lacking constraints such as disentanglement. The joint training enables the image generator to exploit temporal information while the video generation model learns to flexibly share information across frames. Moreover, experimental results verify our approach's compatibility with pre-training on videos or images and training on datasets containing a mixture of both. A comprehensive set of quantitative and qualitative evaluations reveal the improvements in sample quality and diversity over both video generation and image generation baselines. We further demonstrate the technique's capabilities of exploiting similarity in features across frames by applying it to a model based on decomposing the video into motion and content. The proposed model allows minor variations in content across frames while maintaining the temporal dependence through latent vectors encoding the pose or motion features.

TorchGAN: A Flexible Framework for GAN Training and Evaluation

TorchGAN is a PyTorch based framework for writing succinct and comprehensible code for training and evaluation of Generative Adversarial Networks. The framework's modular design allows effortless customization of the model architecture, loss functions, training paradigms, and evaluation metrics. The key features of TorchGAN are its extensibility, built-in support for a large number of popular models, losses and evaluation metrics, and zero overhead compared to vanilla PyTorch. By using the framework to implement several popular GAN models, we demonstrate its extensibility and ease of use. We also benchmark the training time of our framework for said models against the corresponding baseline PyTorch implementations and observe that TorchGAN's features bear almost zero overhead.