NeurInt : Learning to Interpolate through Neural ODEs
Paper and Code
Nov 07, 2021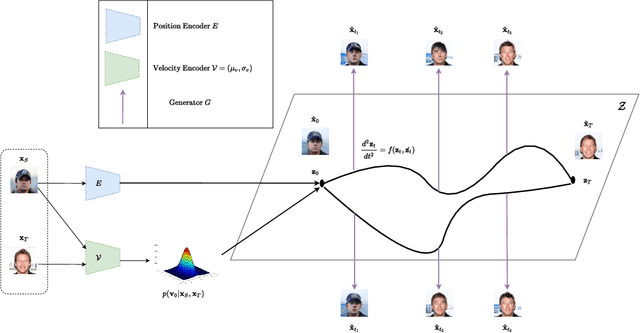
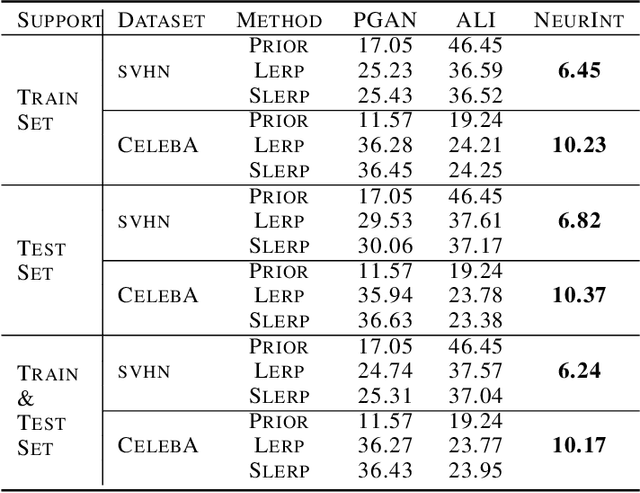


A wide range of applications require learning image generation models whose latent space effectively captures the high-level factors of variation present in the data distribution. The extent to which a model represents such variations through its latent space can be judged by its ability to interpolate between images smoothly. However, most generative models mapping a fixed prior to the generated images lead to interpolation trajectories lacking smoothness and containing images of reduced quality. In this work, we propose a novel generative model that learns a flexible non-parametric prior over interpolation trajectories, conditioned on a pair of source and target images. Instead of relying on deterministic interpolation methods (such as linear or spherical interpolation in latent space), we devise a framework that learns a distribution of trajectories between two given images using Latent Second-Order Neural Ordinary Differential Equations. Through a hybrid combination of reconstruction and adversarial losses, the generator is trained to map the sampled points from these trajectories to sequences of realistic images that smoothly transition from the source to the target image. Through comprehensive qualitative and quantitative experiments, we demonstrate our approach's effectiveness in generating images of improved quality as well as its ability to learn a diverse distribution over smooth interpolation trajectories for any pair of real source and target images.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge