Arun Sai Suggala
Offline-to-online hyperparameter transfer for stochastic bandits
Jan 06, 2025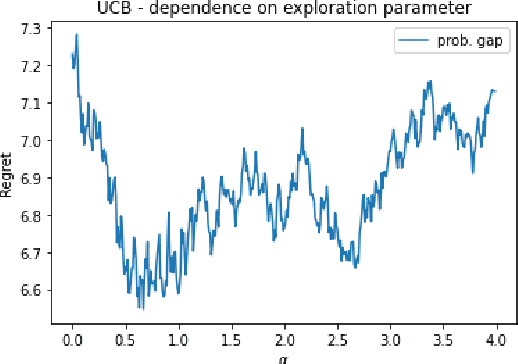

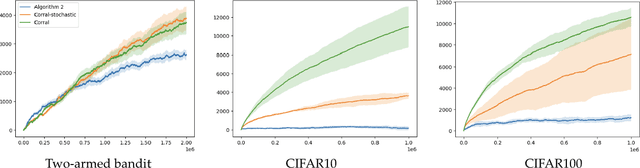
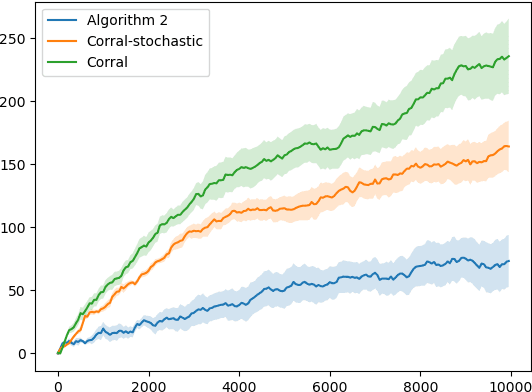
Abstract:Classic algorithms for stochastic bandits typically use hyperparameters that govern their critical properties such as the trade-off between exploration and exploitation. Tuning these hyperparameters is a problem of great practical significance. However, this is a challenging problem and in certain cases is information theoretically impossible. To address this challenge, we consider a practically relevant transfer learning setting where one has access to offline data collected from several bandit problems (tasks) coming from an unknown distribution over the tasks. Our aim is to use this offline data to set the hyperparameters for a new task drawn from the unknown distribution. We provide bounds on the inter-task (number of tasks) and intra-task (number of arm pulls for each task) sample complexity for learning near-optimal hyperparameters on unseen tasks drawn from the distribution. Our results apply to several classic algorithms, including tuning the exploration parameters in UCB and LinUCB and the noise parameter in GP-UCB. Our experiments indicate the significance and effectiveness of the transfer of hyperparameters from offline problems in online learning with stochastic bandit feedback.
CDQuant: Accurate Post-training Weight Quantization of Large Pre-trained Models using Greedy Coordinate Descent
Jun 26, 2024



Abstract:Large language models (LLMs) have recently demonstrated remarkable performance across diverse language tasks. But their deployment is often constrained by their substantial computational and storage requirements. Quantization has emerged as a key technique for addressing this challenge, enabling the compression of large models with minimal impact on performance. The recent GPTQ algorithm, a post-training quantization (PTQ) method, has proven highly effective for compressing LLMs, sparking a wave of research that leverages GPTQ as a core component. Recognizing the pivotal role of GPTQ in the PTQ landscape, we introduce CDQuant, a simple and scalable alternative to GPTQ with improved performance. CDQuant uses coordinate descent to minimize the layer-wise reconstruction loss to achieve high-quality quantized weights. Our algorithm is easy to implement and scales efficiently to models with hundreds of billions of parameters. Through extensive evaluation on the PaLM2 model family, we demonstrate that CDQuant consistently outperforms GPTQ across diverse model sizes and quantization levels. In particular, for INT2 quantization of PaLM2-Otter, CDQuant achieves a 10% reduction in perplexity compared to GPTQ.
Blocked Collaborative Bandits: Online Collaborative Filtering with Per-Item Budget Constraints
Oct 31, 2023

Abstract:We consider the problem of \emph{blocked} collaborative bandits where there are multiple users, each with an associated multi-armed bandit problem. These users are grouped into \emph{latent} clusters such that the mean reward vectors of users within the same cluster are identical. Our goal is to design algorithms that maximize the cumulative reward accrued by all the users over time, under the \emph{constraint} that no arm of a user is pulled more than $\mathsf{B}$ times. This problem has been originally considered by \cite{Bresler:2014}, and designing regret-optimal algorithms for it has since remained an open problem. In this work, we propose an algorithm called \texttt{B-LATTICE} (Blocked Latent bAndiTs via maTrIx ComplEtion) that collaborates across users, while simultaneously satisfying the budget constraints, to maximize their cumulative rewards. Theoretically, under certain reasonable assumptions on the latent structure, with $\mathsf{M}$ users, $\mathsf{N}$ arms, $\mathsf{T}$ rounds per user, and $\mathsf{C}=O(1)$ latent clusters, \texttt{B-LATTICE} achieves a per-user regret of $\widetilde{O}(\sqrt{\mathsf{T}(1 + \mathsf{N}\mathsf{M}^{-1})}$ under a budget constraint of $\mathsf{B}=\Theta(\log \mathsf{T})$. These are the first sub-linear regret bounds for this problem, and match the minimax regret bounds when $\mathsf{B}=\mathsf{T}$. Empirically, we demonstrate that our algorithm has superior performance over baselines even when $\mathsf{B}=1$. \texttt{B-LATTICE} runs in phases where in each phase it clusters users into groups and collaborates across users within a group to quickly learn their reward models.
Stochastic Re-weighted Gradient Descent via Distributionally Robust Optimization
Jun 15, 2023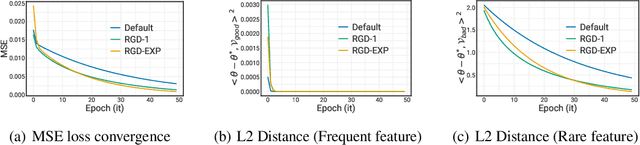


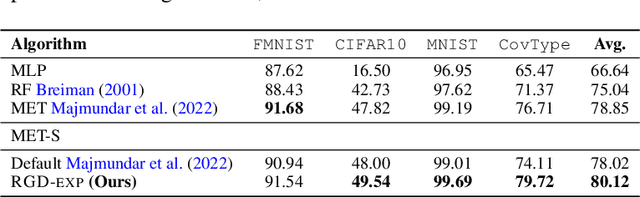
Abstract:We develop a re-weighted gradient descent technique for boosting the performance of deep neural networks. Our algorithm involves the importance weighting of data points during each optimization step. Our approach is inspired by distributionally robust optimization with $f$-divergences, which has been known to result in models with improved generalization guarantees. Our re-weighting scheme is simple, computationally efficient, and can be combined with any popular optimization algorithms such as SGD and Adam. Empirically, we demonstrate our approach's superiority on various tasks, including vanilla classification, classification with label imbalance, noisy labels, domain adaptation, and tabular representation learning. Notably, we obtain improvements of +0.7% and +1.44% over SOTA on DomainBed and Tabular benchmarks, respectively. Moreover, our algorithm boosts the performance of BERT on GLUE benchmarks by +1.94%, and ViT on ImageNet-1K by +0.9%. These results demonstrate the effectiveness of the proposed approach, indicating its potential for improving performance in diverse domains.
Optimal Best-Arm Identification in Bandits with Access to Offline Data
Jun 15, 2023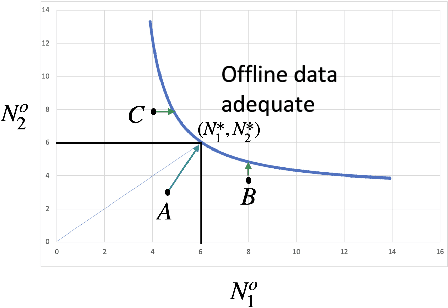
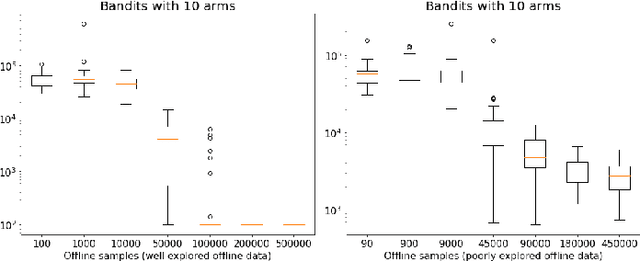
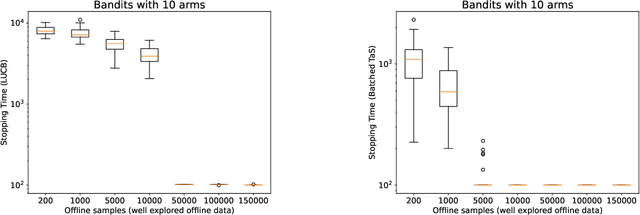
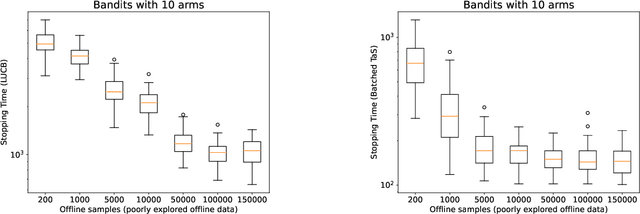
Abstract:Learning paradigms based purely on offline data as well as those based solely on sequential online learning have been well-studied in the literature. In this paper, we consider combining offline data with online learning, an area less studied but of obvious practical importance. We consider the stochastic $K$-armed bandit problem, where our goal is to identify the arm with the highest mean in the presence of relevant offline data, with confidence $1-\delta$. We conduct a lower bound analysis on policies that provide such $1-\delta$ probabilistic correctness guarantees. We develop algorithms that match the lower bound on sample complexity when $\delta$ is small. Our algorithms are computationally efficient with an average per-sample acquisition cost of $\tilde{O}(K)$, and rely on a careful characterization of the optimality conditions of the lower bound problem.
End-to-End Neural Network Compression via $\frac{\ell_1}{\ell_2}$ Regularized Latency Surrogates
Jun 13, 2023



Abstract:Neural network (NN) compression via techniques such as pruning, quantization requires setting compression hyperparameters (e.g., number of channels to be pruned, bitwidths for quantization) for each layer either manually or via neural architecture search (NAS) which can be computationally expensive. We address this problem by providing an end-to-end technique that optimizes for model's Floating Point Operations (FLOPs) or for on-device latency via a novel $\frac{\ell_1}{\ell_2}$ latency surrogate. Our algorithm is versatile and can be used with many popular compression methods including pruning, low-rank factorization, and quantization. Crucially, it is fast and runs in almost the same amount of time as single model training; which is a significant training speed-up over standard NAS methods. For BERT compression on GLUE fine-tuning tasks, we achieve $50\%$ reduction in FLOPs with only $1\%$ drop in performance. For compressing MobileNetV3 on ImageNet-1K, we achieve $15\%$ reduction in FLOPs, and $11\%$ reduction in on-device latency without drop in accuracy, while still requiring $3\times$ less training compute than SOTA compression techniques. Finally, for transfer learning on smaller datasets, our technique identifies $1.2\times$-$1.4\times$ cheaper architectures than standard MobileNetV3, EfficientNet suite of architectures at almost the same training cost and accuracy.
Near Optimal Private and Robust Linear Regression
Jan 30, 2023



Abstract:We study the canonical statistical estimation problem of linear regression from $n$ i.i.d.~examples under $(\varepsilon,\delta)$-differential privacy when some response variables are adversarially corrupted. We propose a variant of the popular differentially private stochastic gradient descent (DP-SGD) algorithm with two innovations: a full-batch gradient descent to improve sample complexity and a novel adaptive clipping to guarantee robustness. When there is no adversarial corruption, this algorithm improves upon the existing state-of-the-art approach and achieves a near optimal sample complexity. Under label-corruption, this is the first efficient linear regression algorithm to guarantee both $(\varepsilon,\delta)$-DP and robustness. Synthetic experiments confirm the superiority of our approach.
Optimal Algorithms for Latent Bandits with Cluster Structure
Jan 17, 2023Abstract:We consider the problem of latent bandits with cluster structure where there are multiple users, each with an associated multi-armed bandit problem. These users are grouped into \emph{latent} clusters such that the mean reward vectors of users within the same cluster are identical. At each round, a user, selected uniformly at random, pulls an arm and observes a corresponding noisy reward. The goal of the users is to maximize their cumulative rewards. This problem is central to practical recommendation systems and has received wide attention of late \cite{gentile2014online, maillard2014latent}. Now, if each user acts independently, then they would have to explore each arm independently and a regret of $\Omega(\sqrt{\mathsf{MNT}})$ is unavoidable, where $\mathsf{M}, \mathsf{N}$ are the number of arms and users, respectively. Instead, we propose LATTICE (Latent bAndiTs via maTrIx ComplEtion) which allows exploitation of the latent cluster structure to provide the minimax optimal regret of $\widetilde{O}(\sqrt{(\mathsf{M}+\mathsf{N})\mathsf{T}})$, when the number of clusters is $\widetilde{O}(1)$. This is the first algorithm to guarantee such a strong regret bound. LATTICE is based on a careful exploitation of arm information within a cluster while simultaneously clustering users. Furthermore, it is computationally efficient and requires only $O(\log{\mathsf{T}})$ calls to an offline matrix completion oracle across all $\mathsf{T}$ rounds.
Building Robust Ensembles via Margin Boosting
Jun 07, 2022
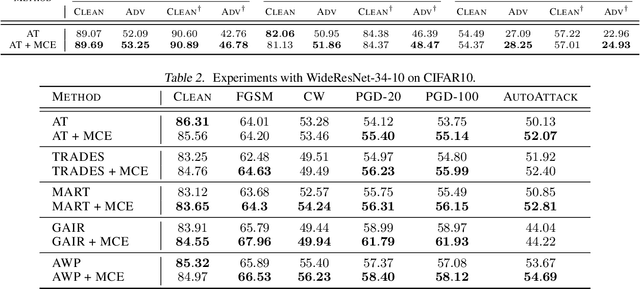

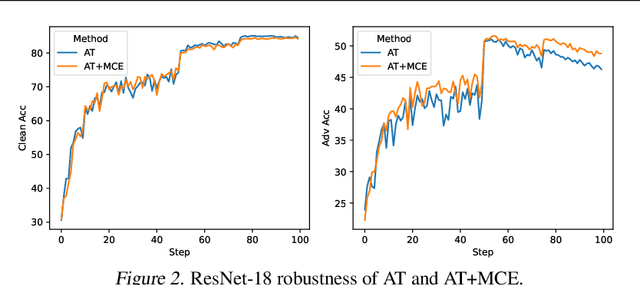
Abstract:In the context of adversarial robustness, a single model does not usually have enough power to defend against all possible adversarial attacks, and as a result, has sub-optimal robustness. Consequently, an emerging line of work has focused on learning an ensemble of neural networks to defend against adversarial attacks. In this work, we take a principled approach towards building robust ensembles. We view this problem from the perspective of margin-boosting and develop an algorithm for learning an ensemble with maximum margin. Through extensive empirical evaluation on benchmark datasets, we show that our algorithm not only outperforms existing ensembling techniques, but also large models trained in an end-to-end fashion. An important byproduct of our work is a margin-maximizing cross-entropy (MCE) loss, which is a better alternative to the standard cross-entropy (CE) loss. Empirically, we show that replacing the CE loss in state-of-the-art adversarial training techniques with our MCE loss leads to significant performance improvement.
Boosted CVaR Classification
Nov 10, 2021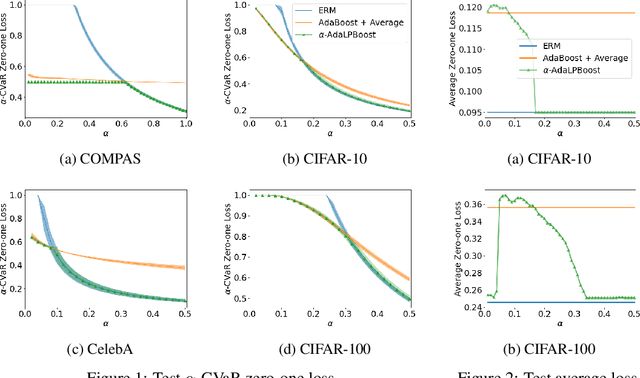
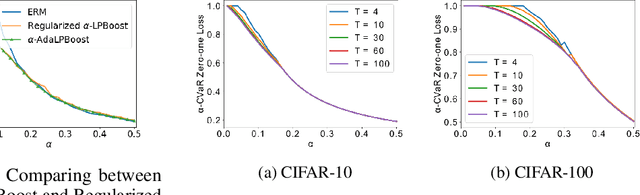
Abstract:Many modern machine learning tasks require models with high tail performance, i.e. high performance over the worst-off samples in the dataset. This problem has been widely studied in fields such as algorithmic fairness, class imbalance, and risk-sensitive decision making. A popular approach to maximize the model's tail performance is to minimize the CVaR (Conditional Value at Risk) loss, which computes the average risk over the tails of the loss. However, for classification tasks where models are evaluated by the zero-one loss, we show that if the classifiers are deterministic, then the minimizer of the average zero-one loss also minimizes the CVaR zero-one loss, suggesting that CVaR loss minimization is not helpful without additional assumptions. We circumvent this negative result by minimizing the CVaR loss over randomized classifiers, for which the minimizers of the average zero-one loss and the CVaR zero-one loss are no longer the same, so minimizing the latter can lead to better tail performance. To learn such randomized classifiers, we propose the Boosted CVaR Classification framework which is motivated by a direct relationship between CVaR and a classical boosting algorithm called LPBoost. Based on this framework, we design an algorithm called $\alpha$-AdaLPBoost. We empirically evaluate our proposed algorithm on four benchmark datasets and show that it achieves higher tail performance than deterministic model training methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge