Optimal Best-Arm Identification in Bandits with Access to Offline Data
Paper and Code
Jun 15, 2023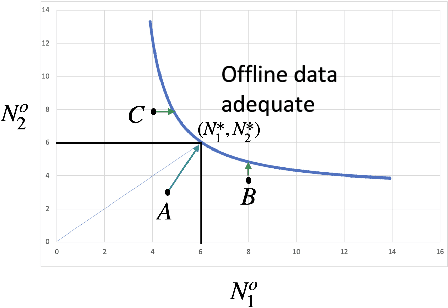
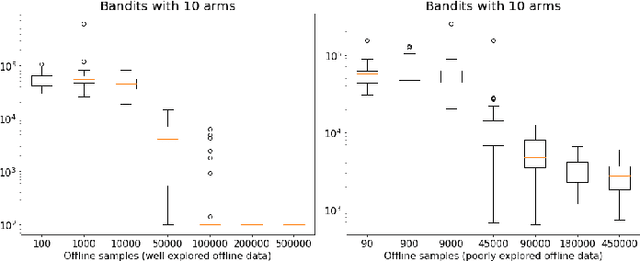
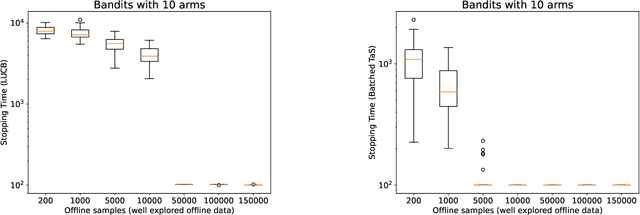
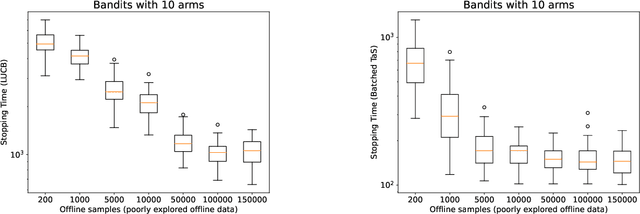
Learning paradigms based purely on offline data as well as those based solely on sequential online learning have been well-studied in the literature. In this paper, we consider combining offline data with online learning, an area less studied but of obvious practical importance. We consider the stochastic $K$-armed bandit problem, where our goal is to identify the arm with the highest mean in the presence of relevant offline data, with confidence $1-\delta$. We conduct a lower bound analysis on policies that provide such $1-\delta$ probabilistic correctness guarantees. We develop algorithms that match the lower bound on sample complexity when $\delta$ is small. Our algorithms are computationally efficient with an average per-sample acquisition cost of $\tilde{O}(K)$, and rely on a careful characterization of the optimality conditions of the lower bound problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge