FastRef:Fast Prototype Refinement for Few-Shot Industrial Anomaly Detection

Few-shot industrial anomaly detection (FS-IAD) presents a critical challenge for practical automated inspection systems operating in data-scarce environments. While existing approaches predominantly focus on deriving prototypes from limited normal samples, they typically neglect to systematically incorporate query image statistics to enhance prototype representativeness. To address this issue, we propose FastRef, a novel and efficient prototype refinement framework for FS-IAD. Our method operates through an iterative two-stage process: (1) characteristic transfer from query features to prototypes via an optimizable transformation matrix, and (2) anomaly suppression through prototype alignment. The characteristic transfer is achieved through linear reconstruction of query features from prototypes, while the anomaly suppression addresses a key observation in FS-IAD that unlike conventional IAD with abundant normal prototypes, the limited-sample setting makes anomaly reconstruction more probable. Therefore, we employ optimal transport (OT) for non-Gaussian sampled features to measure and minimize the gap between prototypes and their refined counterparts for anomaly suppression. For comprehensive evaluation, we integrate FastRef with three competitive prototype-based FS-IAD methods: PatchCore, FastRecon, WinCLIP, and AnomalyDINO. Extensive experiments across four benchmark datasets of MVTec, ViSA, MPDD and RealIAD demonstrate both the effectiveness and computational efficiency of our approach under 1/2/4-shots.

Meta-SurDiff: Classification Diffusion Model Optimized by Meta Learning is Reliable for Online Surgical Phase Recognition

Online surgical phase recognition has drawn great attention most recently due to its potential downstream applications closely related to human life and health. Despite deep models have made significant advances in capturing the discriminative long-term dependency of surgical videos to achieve improved recognition, they rarely account for exploring and modeling the uncertainty in surgical videos, which should be crucial for reliable online surgical phase recognition. We categorize the sources of uncertainty into two types, frame ambiguity in videos and unbalanced distribution among surgical phases, which are inevitable in surgical videos. To address this pivot issue, we introduce a meta-learning-optimized classification diffusion model (Meta-SurDiff), to take full advantage of the deep generative model and meta-learning in achieving precise frame-level distribution estimation for reliable online surgical phase recognition. For coarse recognition caused by ambiguous video frames, we employ a classification diffusion model to assess the confidence of recognition results at a finer-grained frame-level instance. For coarse recognition caused by unbalanced phase distribution, we use a meta-learning based objective to learn the diffusion model, thus enhancing the robustness of classification boundaries for different surgical phases.We establish effectiveness of Meta-SurDiff in online surgical phase recognition through extensive experiments on five widely used datasets using more than four practical metrics. The datasets include Cholec80, AutoLaparo, M2Cai16, OphNet, and NurViD, where OphNet comes from ophthalmic surgeries, NurViD is the daily care dataset, while the others come from laparoscopic surgeries. We will release the code upon acceptance.

Insufficient Statistics Perturbation: Stable Estimators for Private Least Squares

We present a sample- and time-efficient differentially private algorithm for ordinary least squares, with error that depends linearly on the dimension and is independent of the condition number of $X^\top X$, where $X$ is the design matrix. All prior private algorithms for this task require either $d^{3/2}$ examples, error growing polynomially with the condition number, or exponential time. Our near-optimal accuracy guarantee holds for any dataset with bounded statistical leverage and bounded residuals. Technically, we build on the approach of Brown et al. (2023) for private mean estimation, adding scaled noise to a carefully designed stable nonprivate estimator of the empirical regression vector.

Hierarchical Vector Quantized Transformer for Multi-class Unsupervised Anomaly Detection

Unsupervised image Anomaly Detection (UAD) aims to learn robust and discriminative representations of normal samples. While separate solutions per class endow expensive computation and limited generalizability, this paper focuses on building a unified framework for multiple classes. Under such a challenging setting, popular reconstruction-based networks with continuous latent representation assumption always suffer from the "identical shortcut" issue, where both normal and abnormal samples can be well recovered and difficult to distinguish. To address this pivotal issue, we propose a hierarchical vector quantized prototype-oriented Transformer under a probabilistic framework. First, instead of learning the continuous representations, we preserve the typical normal patterns as discrete iconic prototypes, and confirm the importance of Vector Quantization in preventing the model from falling into the shortcut. The vector quantized iconic prototype is integrated into the Transformer for reconstruction, such that the abnormal data point is flipped to a normal data point.Second, we investigate an exquisite hierarchical framework to relieve the codebook collapse issue and replenish frail normal patterns. Third, a prototype-oriented optimal transport method is proposed to better regulate the prototypes and hierarchically evaluate the abnormal score. By evaluating on MVTec-AD and VisA datasets, our model surpasses the state-of-the-art alternatives and possesses good interpretability. The code is available at https://github.com/RuiyingLu/HVQ-Trans.

Prototypes-oriented Transductive Few-shot Learning with Conditional Transport

Transductive Few-Shot Learning (TFSL) has recently attracted increasing attention since it typically outperforms its inductive peer by leveraging statistics of query samples. However, previous TFSL methods usually encode uniform prior that all the classes within query samples are equally likely, which is biased in imbalanced TFSL and causes severe performance degradation. Given this pivotal issue, in this work, we propose a novel Conditional Transport (CT) based imbalanced TFSL model called {\textbf P}rototypes-oriented {\textbf U}nbiased {\textbf T}ransfer {\textbf M}odel (PUTM) to fully exploit unbiased statistics of imbalanced query samples, which employs forward and backward navigators as transport matrices to balance the prior of query samples per class between uniform and adaptive data-driven distributions. For efficiently transferring statistics learned by CT, we further derive a closed form solution to refine prototypes based on MAP given the learned navigators. The above two steps of discovering and transferring unbiased statistics follow an iterative manner, formulating our EM-based solver. Experimental results on four standard benchmarks including miniImageNet, tieredImageNet, CUB, and CIFAR-FS demonstrate superiority of our model in class-imbalanced generalization.

Near Optimal Private and Robust Linear Regression

We study the canonical statistical estimation problem of linear regression from $n$ i.i.d.~examples under $(\varepsilon,\delta)$-differential privacy when some response variables are adversarially corrupted. We propose a variant of the popular differentially private stochastic gradient descent (DP-SGD) algorithm with two innovations: a full-batch gradient descent to improve sample complexity and a novel adaptive clipping to guarantee robustness. When there is no adversarial corruption, this algorithm improves upon the existing state-of-the-art approach and achieves a near optimal sample complexity. Under label-corruption, this is the first efficient linear regression algorithm to guarantee both $(\varepsilon,\delta)$-DP and robustness. Synthetic experiments confirm the superiority of our approach.

Machine Learning-Aided Efficient Decoding of Reed-Muller Subcodes

Reed-Muller (RM) codes achieve the capacity of general binary-input memoryless symmetric channels and have a comparable performance to that of random codes in terms of scaling laws. However, they lack efficient decoders with performance close to that of a maximum-likelihood decoder for general code parameters. Also, they only admit limited sets of rates. In this paper, we focus on subcodes of RM codes with flexible rates. We first extend the recently-introduced recursive projection-aggregation (RPA) decoding algorithm to RM subcodes. To lower the complexity of our decoding algorithm, referred to as subRPA, we investigate different approaches to prune the projections. Next, we derive the soft-decision based version of our algorithm, called soft-subRPA, that not only improves upon the performance of subRPA but also enables a differentiable decoding algorithm. Building upon the soft-subRPA algorithm, we then provide a framework for training a machine learning (ML) model to search for \textit{good} sets of projections that minimize the decoding error rate. Training our ML model enables achieving very close to the performance of full-projection decoding with a significantly smaller number of projections. We also show that the choice of the projections in decoding RM subcodes matters significantly, and our ML-aided projection pruning scheme is able to find a \textit{good} selection, i.e., with negligible performance degradation compared to the full-projection case, given a reasonable number of projections.

DP-PCA: Statistically Optimal and Differentially Private PCA

We study the canonical statistical task of computing the principal component from $n$ i.i.d.~data in $d$ dimensions under $(\varepsilon,\delta)$-differential privacy. Although extensively studied in literature, existing solutions fall short on two key aspects: ($i$) even for Gaussian data, existing private algorithms require the number of samples $n$ to scale super-linearly with $d$, i.e., $n=\Omega(d^{3/2})$, to obtain non-trivial results while non-private PCA requires only $n=O(d)$, and ($ii$) existing techniques suffer from a non-vanishing error even when the randomness in each data point is arbitrarily small. We propose DP-PCA, which is a single-pass algorithm that overcomes both limitations. It is based on a private minibatch gradient ascent method that relies on {\em private mean estimation}, which adds minimal noise required to ensure privacy by adapting to the variance of a given minibatch of gradients. For sub-Gaussian data, we provide nearly optimal statistical error rates even for $n=\tilde O(d)$. Furthermore, we provide a lower bound showing that sub-Gaussian style assumption is necessary in obtaining the optimal error rate.

Differential privacy and robust statistics in high dimensions

We introduce a universal framework for characterizing the statistical efficiency of a statistical estimation problem with differential privacy guarantees. Our framework, which we call High-dimensional Propose-Test-Release (HPTR), builds upon three crucial components: the exponential mechanism, robust statistics, and the Propose-Test-Release mechanism. Gluing all these together is the concept of resilience, which is central to robust statistical estimation. Resilience guides the design of the algorithm, the sensitivity analysis, and the success probability analysis of the test step in Propose-Test-Release. The key insight is that if we design an exponential mechanism that accesses the data only via one-dimensional robust statistics, then the resulting local sensitivity can be dramatically reduced. Using resilience, we can provide tight local sensitivity bounds. These tight bounds readily translate into near-optimal utility guarantees in several cases. We give a general recipe for applying HPTR to a given instance of a statistical estimation problem and demonstrate it on canonical problems of mean estimation, linear regression, covariance estimation, and principal component analysis. We introduce a general utility analysis technique that proves that HPTR nearly achieves the optimal sample complexity under several scenarios studied in the literature.

KO codes: Inventing Nonlinear Encoding and Decoding for Reliable Wireless Communication via Deep-learning

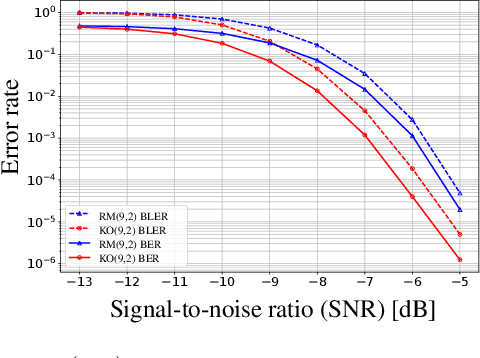
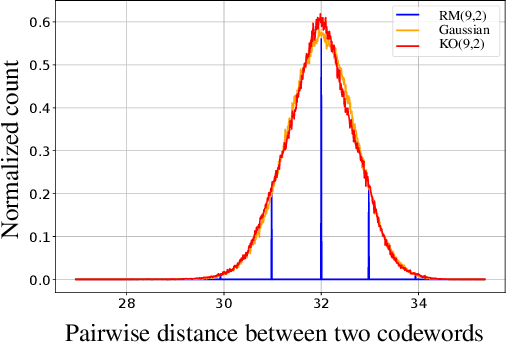
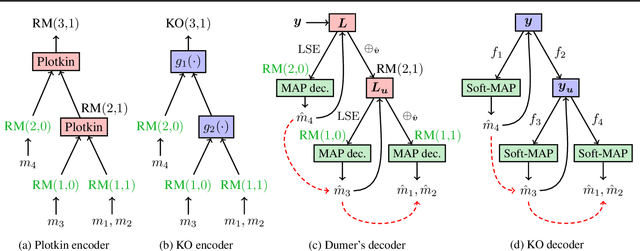
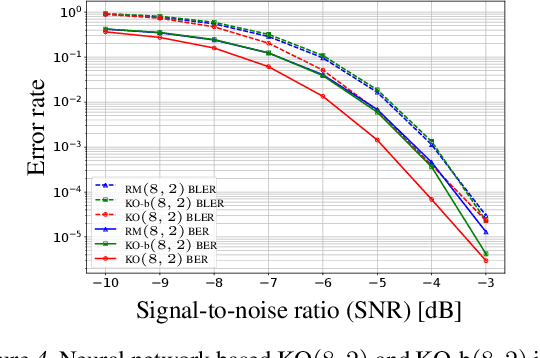
Landmark codes underpin reliable physical layer communication, e.g., Reed-Muller, BCH, Convolution, Turbo, LDPC and Polar codes: each is a linear code and represents a mathematical breakthrough. The impact on humanity is huge: each of these codes has been used in global wireless communication standards (satellite, WiFi, cellular). Reliability of communication over the classical additive white Gaussian noise (AWGN) channel enables benchmarking and ranking of the different codes. In this paper, we construct KO codes, a computationaly efficient family of deep-learning driven (encoder, decoder) pairs that outperform the state-of-the-art reliability performance on the standardized AWGN channel. KO codes beat state-of-the-art Reed-Muller and Polar codes, under the low-complexity successive cancellation decoding, in the challenging short-to-medium block length regime on the AWGN channel. We show that the gains of KO codes are primarily due to the nonlinear mapping of information bits directly to transmit real symbols (bypassing modulation) and yet possess an efficient, high performance decoder. The key technical innovation that renders this possible is design of a novel family of neural architectures inspired by the computation tree of the {\bf K}ronecker {\bf O}peration (KO) central to Reed-Muller and Polar codes. These architectures pave way for the discovery of a much richer class of hitherto unexplored nonlinear algebraic structures. The code is available at \href{https://github.com/deepcomm/KOcodes}{https://github.com/deepcomm/KOcodes}