ProductAE: Toward Deep Learning Driven Error-Correction Codes of Large Dimensions

While decades of theoretical research have led to the invention of several classes of error-correction codes, the design of such codes is an extremely challenging task, mostly driven by human ingenuity. Recent studies demonstrate that such designs can be effectively automated and accelerated via tools from machine learning (ML), thus enabling ML-driven classes of error-correction codes with promising performance gains compared to classical designs. A fundamental challenge, however, is that it is prohibitively complex, if not impossible, to design and train fully ML-driven encoder and decoder pairs for large code dimensions. In this paper, we propose Product Autoencoder (ProductAE) -- a computationally-efficient family of deep learning driven (encoder, decoder) pairs -- aimed at enabling the training of relatively large codes (both encoder and decoder) with a manageable training complexity. We build upon ideas from classical product codes and propose constructing large neural codes using smaller code components. ProductAE boils down the complex problem of training the encoder and decoder for a large code dimension $k$ and blocklength $n$ to less-complex sub-problems of training encoders and decoders for smaller dimensions and blocklengths. Our training results show successful training of ProductAEs of dimensions as large as $k = 300$ bits with meaningful performance gains compared to state-of-the-art classical and neural designs. Moreover, we demonstrate excellent robustness and adaptivity of ProductAEs to channel models different than the ones used for training.

Machine Learning-Aided Efficient Decoding of Reed-Muller Subcodes

Reed-Muller (RM) codes achieve the capacity of general binary-input memoryless symmetric channels and have a comparable performance to that of random codes in terms of scaling laws. However, they lack efficient decoders with performance close to that of a maximum-likelihood decoder for general code parameters. Also, they only admit limited sets of rates. In this paper, we focus on subcodes of RM codes with flexible rates. We first extend the recently-introduced recursive projection-aggregation (RPA) decoding algorithm to RM subcodes. To lower the complexity of our decoding algorithm, referred to as subRPA, we investigate different approaches to prune the projections. Next, we derive the soft-decision based version of our algorithm, called soft-subRPA, that not only improves upon the performance of subRPA but also enables a differentiable decoding algorithm. Building upon the soft-subRPA algorithm, we then provide a framework for training a machine learning (ML) model to search for \textit{good} sets of projections that minimize the decoding error rate. Training our ML model enables achieving very close to the performance of full-projection decoding with a significantly smaller number of projections. We also show that the choice of the projections in decoding RM subcodes matters significantly, and our ML-aided projection pruning scheme is able to find a \textit{good} selection, i.e., with negligible performance degradation compared to the full-projection case, given a reasonable number of projections.

ProductAE: Towards Training Larger Channel Codes based on Neural Product Codes

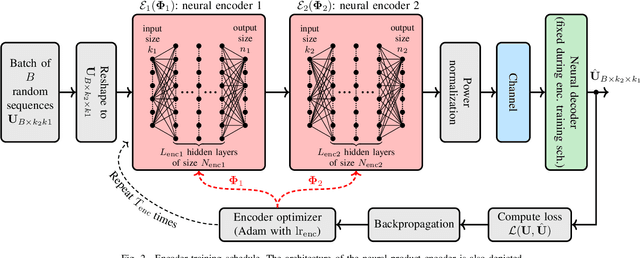
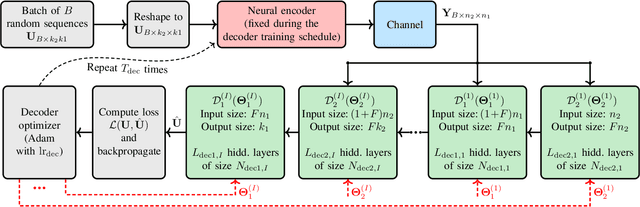
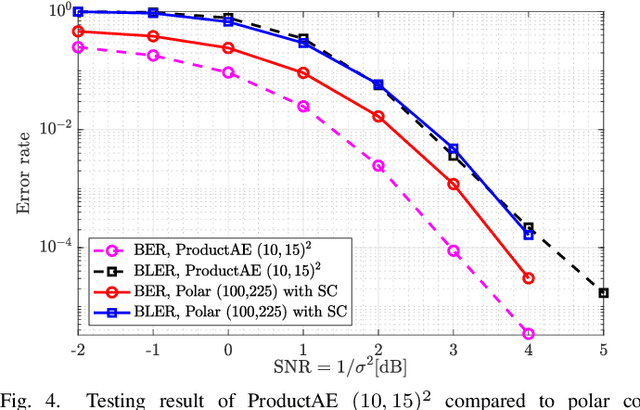
There have been significant research activities in recent years to automate the design of channel encoders and decoders via deep learning. Due the dimensionality challenge in channel coding, it is prohibitively complex to design and train relatively large neural channel codes via deep learning techniques. Consequently, most of the results in the literature are limited to relatively short codes having less than 100 information bits. In this paper, we construct ProductAEs, a computationally efficient family of deep-learning driven (encoder, decoder) pairs, that aim at enabling the training of relatively large channel codes (both encoders and decoders) with a manageable training complexity. We build upon the ideas from classical product codes, and propose constructing large neural codes using smaller code components. More specifically, instead of directly training the encoder and decoder for a large neural code of dimension $k$ and blocklength $n$, we provide a framework that requires training neural encoders and decoders for the code parameters $(k_1,n_1)$ and $(k_2,n_2)$ such that $k_1 k_2=k$ and $n_1 n_2=n$. Our training results show significant gains, over all ranges of signal-to-noise ratio (SNR), for a code of parameters $(100,225)$ and a moderate-length code of parameters $(196,441)$, over polar codes under successive cancellation (SC) decoder. Moreover, our results demonstrate meaningful gains over Turbo Autoencoder (TurboAE) and state-of-the-art classical codes. This is the first work to design product autoencoders and a pioneering work on training large channel codes.

KO codes: Inventing Nonlinear Encoding and Decoding for Reliable Wireless Communication via Deep-learning

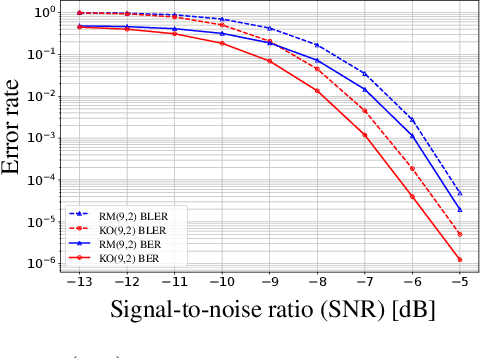
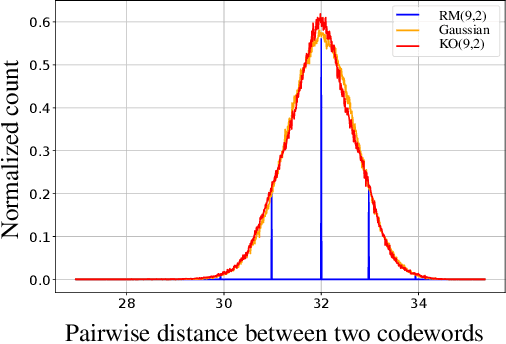
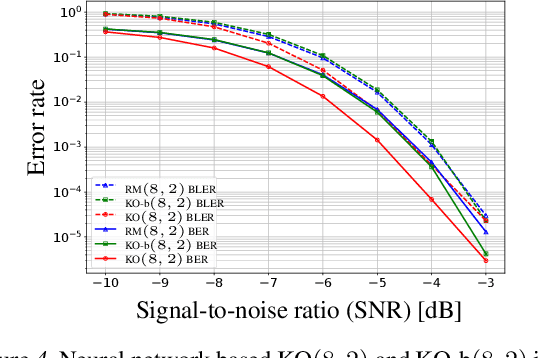
Landmark codes underpin reliable physical layer communication, e.g., Reed-Muller, BCH, Convolution, Turbo, LDPC and Polar codes: each is a linear code and represents a mathematical breakthrough. The impact on humanity is huge: each of these codes has been used in global wireless communication standards (satellite, WiFi, cellular). Reliability of communication over the classical additive white Gaussian noise (AWGN) channel enables benchmarking and ranking of the different codes. In this paper, we construct KO codes, a computationaly efficient family of deep-learning driven (encoder, decoder) pairs that outperform the state-of-the-art reliability performance on the standardized AWGN channel. KO codes beat state-of-the-art Reed-Muller and Polar codes, under the low-complexity successive cancellation decoding, in the challenging short-to-medium block length regime on the AWGN channel. We show that the gains of KO codes are primarily due to the nonlinear mapping of information bits directly to transmit real symbols (bypassing modulation) and yet possess an efficient, high performance decoder. The key technical innovation that renders this possible is design of a novel family of neural architectures inspired by the computation tree of the {\bf K}ronecker {\bf O}peration (KO) central to Reed-Muller and Polar codes. These architectures pave way for the discovery of a much richer class of hitherto unexplored nonlinear algebraic structures. The code is available at \href{https://github.com/deepcomm/KOcodes}{https://github.com/deepcomm/KOcodes}