p-Mean Regret for Stochastic Bandits

In this work, we extend the concept of the $p$-mean welfare objective from social choice theory (Moulin 2004) to study $p$-mean regret in stochastic multi-armed bandit problems. The $p$-mean regret, defined as the difference between the optimal mean among the arms and the $p$-mean of the expected rewards, offers a flexible framework for evaluating bandit algorithms, enabling algorithm designers to balance fairness and efficiency by adjusting the parameter $p$. Our framework encompasses both average cumulative regret and Nash regret as special cases. We introduce a simple, unified UCB-based algorithm (Explore-Then-UCB) that achieves novel $p$-mean regret bounds. Our algorithm consists of two phases: a carefully calibrated uniform exploration phase to initialize sample means, followed by the UCB1 algorithm of Auer, Cesa-Bianchi, and Fischer (2002). Under mild assumptions, we prove that our algorithm achieves a $p$-mean regret bound of $\tilde{O}\left(\sqrt{\frac{k}{T^{\frac{1}{2|p|}}}}\right)$ for all $p \leq -1$, where $k$ represents the number of arms and $T$ the time horizon. When $-1<p<0$, we achieve a regret bound of $\tilde{O}\left(\sqrt{\frac{k^{1.5}}{T^{\frac{1}{2}}}}\right)$. For the range $0< p \leq 1$, we achieve a $p$-mean regret scaling as $\tilde{O}\left(\sqrt{\frac{k}{T}}\right)$, which matches the previously established lower bound up to logarithmic factors (Auer et al. 1995). This result stems from the fact that the $p$-mean regret of any algorithm is at least its average cumulative regret for $p \leq 1$. In the case of Nash regret (the limit as $p$ approaches zero), our unified approach differs from prior work (Barman et al. 2023), which requires a new Nash Confidence Bound algorithm. Notably, we achieve the same regret bound up to constant factors using our more general method.

Learning multivariate Gaussians with imperfect advice

We revisit the problem of distribution learning within the framework of learning-augmented algorithms. In this setting, we explore the scenario where a probability distribution is provided as potentially inaccurate advice on the true, unknown distribution. Our objective is to develop learning algorithms whose sample complexity decreases as the quality of the advice improves, thereby surpassing standard learning lower bounds when the advice is sufficiently accurate. Specifically, we demonstrate that this outcome is achievable for the problem of learning a multivariate Gaussian distribution $N(\boldsymbol{\mu}, \boldsymbol{\Sigma})$ in the PAC learning setting. Classically, in the advice-free setting, $\tilde{\Theta}(d^2/\varepsilon^2)$ samples are sufficient and worst case necessary to learn $d$-dimensional Gaussians up to TV distance $\varepsilon$ with constant probability. When we are additionally given a parameter $\tilde{\boldsymbol{\Sigma}}$ as advice, we show that $\tilde{O}(d^{2-\beta}/\varepsilon^2)$ samples suffices whenever $\| \tilde{\boldsymbol{\Sigma}}^{-1/2} \boldsymbol{\Sigma} \tilde{\boldsymbol{\Sigma}}^{-1/2} - \boldsymbol{I_d} \|_1 \leq \varepsilon d^{1-\beta}$ (where $\|\cdot\|_1$ denotes the entrywise $\ell_1$ norm) for any $\beta > 0$, yielding a polynomial improvement over the advice-free setting.

Efficient, Low-Regret, Online Reinforcement Learning for Linear MDPs

Reinforcement learning algorithms are usually stated without theoretical guarantees regarding their performance. Recently, Jin, Yang, Wang, and Jordan (COLT 2020) showed a polynomial-time reinforcement learning algorithm (namely, LSVI-UCB) for the setting of linear Markov decision processes, and provided theoretical guarantees regarding its running time and regret. In real-world scenarios, however, the space usage of this algorithm can be prohibitive due to a utilized linear regression step. We propose and analyze two modifications of LSVI-UCB, which alternate periods of learning and not-learning, to reduce space and time usage while maintaining sublinear regret. We show experimentally, on synthetic data and real-world benchmarks, that our algorithms achieve low space usage and running time, while not significantly sacrificing regret.

Distribution Learning Meets Graph Structure Sampling

This work establishes a novel link between the problem of PAC-learning high-dimensional graphical models and the task of (efficient) counting and sampling of graph structures, using an online learning framework. We observe that if we apply the exponentially weighted average (EWA) or randomized weighted majority (RWM) forecasters on a sequence of samples from a distribution P using the log loss function, the average regret incurred by the forecaster's predictions can be used to bound the expected KL divergence between P and the predictions. Known regret bounds for EWA and RWM then yield new sample complexity bounds for learning Bayes nets. Moreover, these algorithms can be made computationally efficient for several interesting classes of Bayes nets. Specifically, we give a new sample-optimal and polynomial time learning algorithm with respect to trees of unknown structure and the first polynomial sample and time algorithm for learning with respect to Bayes nets over a given chordal skeleton.

Verifying Individual Fairness in Machine Learning Models

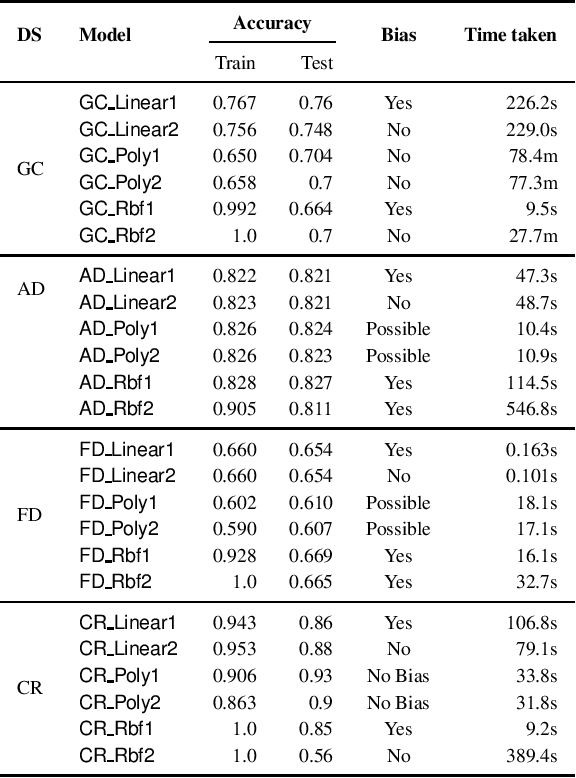
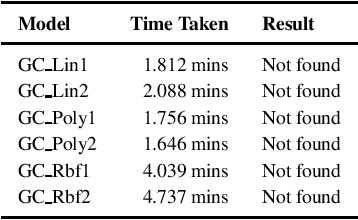
We consider the problem of whether a given decision model, working with structured data, has individual fairness. Following the work of Dwork, a model is individually biased (or unfair) if there is a pair of valid inputs which are close to each other (according to an appropriate metric) but are treated differently by the model (different class label, or large difference in output), and it is unbiased (or fair) if no such pair exists. Our objective is to construct verifiers for proving individual fairness of a given model, and we do so by considering appropriate relaxations of the problem. We construct verifiers which are sound but not complete for linear classifiers, and kernelized polynomial/radial basis function classifiers. We also report the experimental results of evaluating our proposed algorithms on publicly available datasets.