Verifying Individual Fairness in Machine Learning Models
Paper and Code
Jun 21, 2020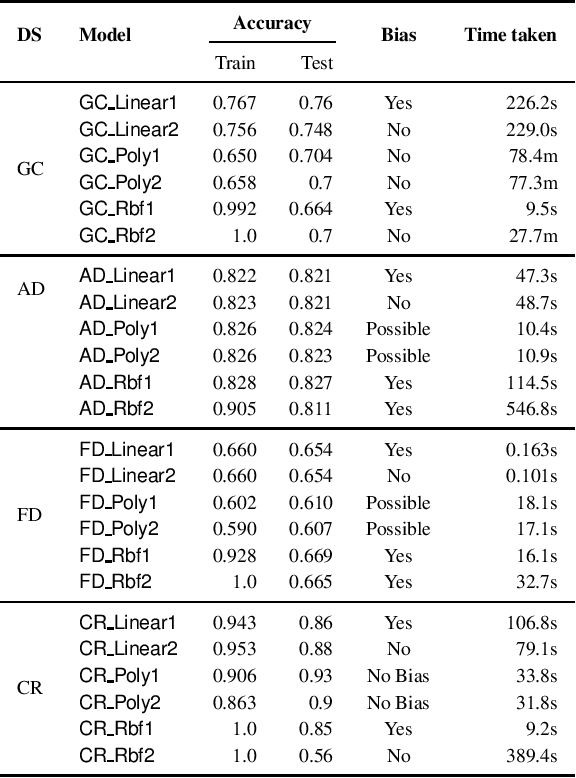
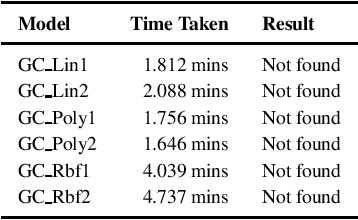

We consider the problem of whether a given decision model, working with structured data, has individual fairness. Following the work of Dwork, a model is individually biased (or unfair) if there is a pair of valid inputs which are close to each other (according to an appropriate metric) but are treated differently by the model (different class label, or large difference in output), and it is unbiased (or fair) if no such pair exists. Our objective is to construct verifiers for proving individual fairness of a given model, and we do so by considering appropriate relaxations of the problem. We construct verifiers which are sound but not complete for linear classifiers, and kernelized polynomial/radial basis function classifiers. We also report the experimental results of evaluating our proposed algorithms on publicly available datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge