Everything, Everywhere, All at Once: Is Mechanistic Interpretability Identifiable?

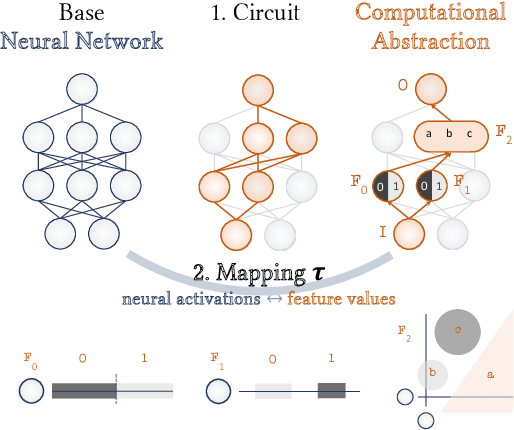
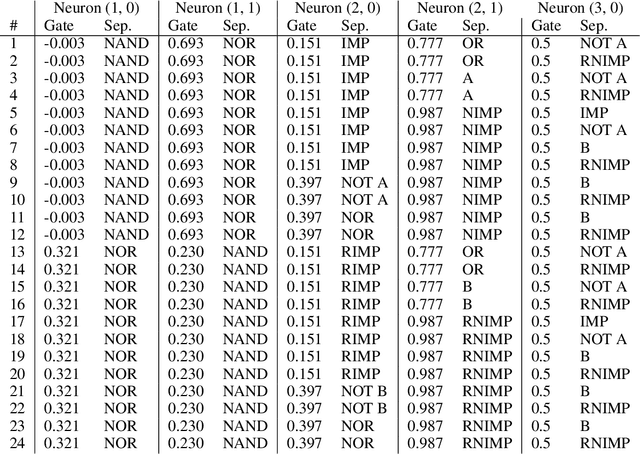
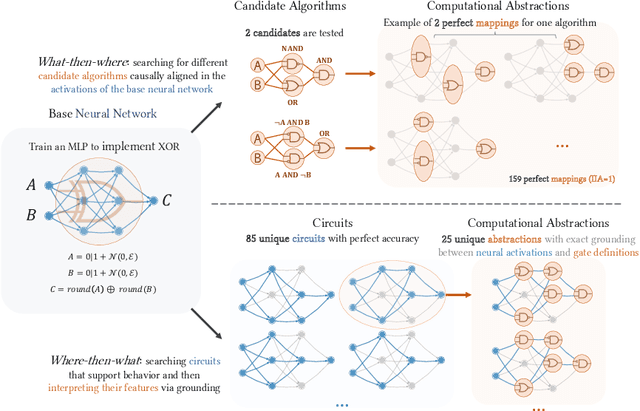
As AI systems are used in high-stakes applications, ensuring interpretability is crucial. Mechanistic Interpretability (MI) aims to reverse-engineer neural networks by extracting human-understandable algorithms to explain their behavior. This work examines a key question: for a given behavior, and under MI's criteria, does a unique explanation exist? Drawing on identifiability in statistics, where parameters are uniquely inferred under specific assumptions, we explore the identifiability of MI explanations. We identify two main MI strategies: (1) "where-then-what," which isolates a circuit replicating model behavior before interpreting it, and (2) "what-then-where," which starts with candidate algorithms and searches for neural activation subspaces implementing them, using causal alignment. We test both strategies on Boolean functions and small multi-layer perceptrons, fully enumerating candidate explanations. Our experiments reveal systematic non-identifiability: multiple circuits can replicate behavior, a circuit can have multiple interpretations, several algorithms can align with the network, and one algorithm can align with different subspaces. Is uniqueness necessary? A pragmatic approach may require only predictive and manipulability standards. If uniqueness is essential for understanding, stricter criteria may be needed. We also reference the inner interpretability framework, which validates explanations through multiple criteria. This work contributes to defining explanation standards in AI.

Efficient, Low-Regret, Online Reinforcement Learning for Linear MDPs

Reinforcement learning algorithms are usually stated without theoretical guarantees regarding their performance. Recently, Jin, Yang, Wang, and Jordan (COLT 2020) showed a polynomial-time reinforcement learning algorithm (namely, LSVI-UCB) for the setting of linear Markov decision processes, and provided theoretical guarantees regarding its running time and regret. In real-world scenarios, however, the space usage of this algorithm can be prohibitive due to a utilized linear regression step. We propose and analyze two modifications of LSVI-UCB, which alternate periods of learning and not-learning, to reduce space and time usage while maintaining sublinear regret. We show experimentally, on synthetic data and real-world benchmarks, that our algorithms achieve low space usage and running time, while not significantly sacrificing regret.

Contextual Bandits for Advertising Campaigns: A Diffusion-Model Independent Approach (Extended Version)

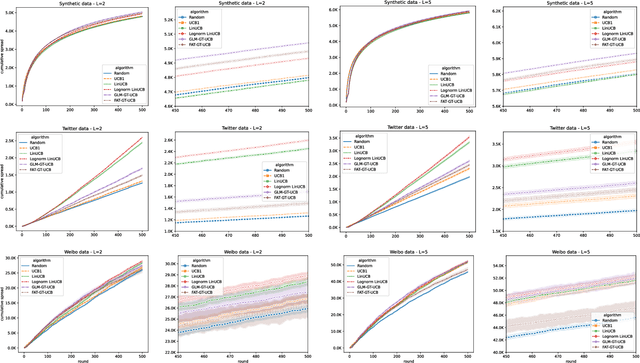
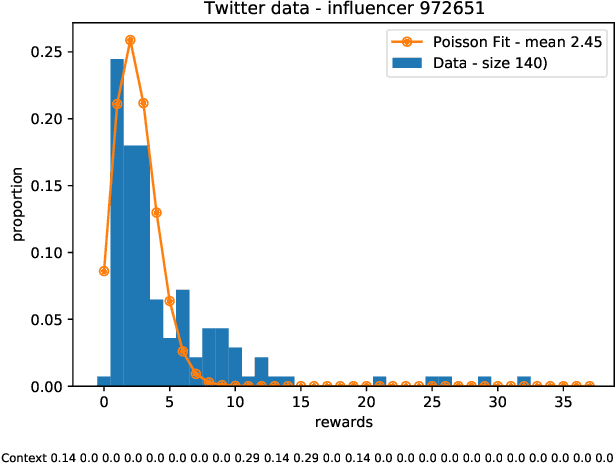
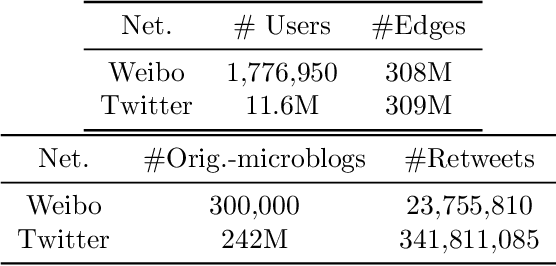
Motivated by scenarios of information diffusion and advertising in social media, we study an influence maximization problem in which little is assumed to be known about the diffusion network or about the model that determines how information may propagate. In such a highly uncertain environment, one can focus on multi-round diffusion campaigns, with the objective to maximize the number of distinct users that are influenced or activated, starting from a known base of few influential nodes. During a campaign, spread seeds are selected sequentially at consecutive rounds, and feedback is collected in the form of the activated nodes at each round. A round's impact (reward) is then quantified as the number of newly activated nodes. Overall, one must maximize the campaign's total spread, as the sum of rounds' rewards. In this setting, an explore-exploit approach could be used to learn the key underlying diffusion parameters, while running the campaign. We describe and compare two methods of contextual multi-armed bandits, with upper-confidence bounds on the remaining potential of influencers, one using a generalized linear model and the Good-Turing estimator for remaining potential (GLM-GT-UCB), and another one that directly adapts the LinUCB algorithm to our setting (LogNorm-LinUCB). We show that they outperform baseline methods using state-of-the-art ideas, on synthetic and real-world data, while at the same time exhibiting different and complementary behavior, depending on the scenarios in which they are deployed.

Bandits Under The Influence (Extended Version)

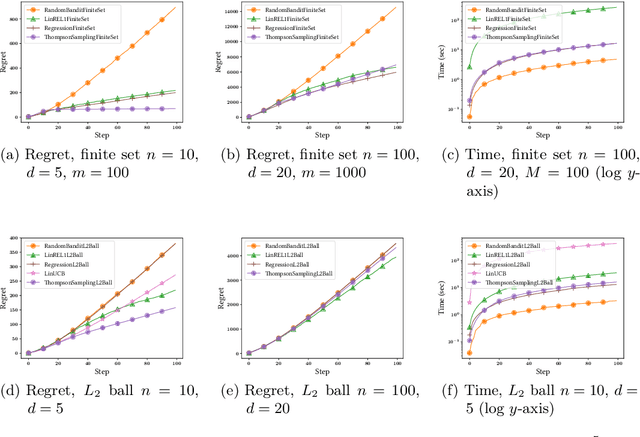
Recommender systems should adapt to user interests as the latter evolve. A prevalent cause for the evolution of user interests is the influence of their social circle. In general, when the interests are not known, online algorithms that explore the recommendation space while also exploiting observed preferences are preferable. We present online recommendation algorithms rooted in the linear multi-armed bandit literature. Our bandit algorithms are tailored precisely to recommendation scenarios where user interests evolve under social influence. In particular, we show that our adaptations of the classic LinREL and Thompson Sampling algorithms maintain the same asymptotic regret bounds as in the non-social case. We validate our approach experimentally using both synthetic and real datasets.