p-Mean Regret for Stochastic Bandits

In this work, we extend the concept of the $p$-mean welfare objective from social choice theory (Moulin 2004) to study $p$-mean regret in stochastic multi-armed bandit problems. The $p$-mean regret, defined as the difference between the optimal mean among the arms and the $p$-mean of the expected rewards, offers a flexible framework for evaluating bandit algorithms, enabling algorithm designers to balance fairness and efficiency by adjusting the parameter $p$. Our framework encompasses both average cumulative regret and Nash regret as special cases. We introduce a simple, unified UCB-based algorithm (Explore-Then-UCB) that achieves novel $p$-mean regret bounds. Our algorithm consists of two phases: a carefully calibrated uniform exploration phase to initialize sample means, followed by the UCB1 algorithm of Auer, Cesa-Bianchi, and Fischer (2002). Under mild assumptions, we prove that our algorithm achieves a $p$-mean regret bound of $\tilde{O}\left(\sqrt{\frac{k}{T^{\frac{1}{2|p|}}}}\right)$ for all $p \leq -1$, where $k$ represents the number of arms and $T$ the time horizon. When $-1<p<0$, we achieve a regret bound of $\tilde{O}\left(\sqrt{\frac{k^{1.5}}{T^{\frac{1}{2}}}}\right)$. For the range $0< p \leq 1$, we achieve a $p$-mean regret scaling as $\tilde{O}\left(\sqrt{\frac{k}{T}}\right)$, which matches the previously established lower bound up to logarithmic factors (Auer et al. 1995). This result stems from the fact that the $p$-mean regret of any algorithm is at least its average cumulative regret for $p \leq 1$. In the case of Nash regret (the limit as $p$ approaches zero), our unified approach differs from prior work (Barman et al. 2023), which requires a new Nash Confidence Bound algorithm. Notably, we achieve the same regret bound up to constant factors using our more general method.

A Sample Efficient Alternating Minimization-based Algorithm For Robust Phase Retrieval

In this work, we study the robust phase retrieval problem where the task is to recover an unknown signal $\theta^* \in \mathbb{R}^d$ in the presence of potentially arbitrarily corrupted magnitude-only linear measurements. We propose an alternating minimization approach that incorporates an oracle solver for a non-convex optimization problem as a subroutine. Our algorithm guarantees convergence to $\theta^*$ and provides an explicit polynomial dependence of the convergence rate on the fraction of corrupted measurements. We then provide an efficient construction of the aforementioned oracle under a sparse arbitrary outliers model and offer valuable insights into the geometric properties of the loss landscape in phase retrieval with corrupted measurements. Our proposed oracle avoids the need for computationally intensive spectral initialization, using a simple gradient descent algorithm with a constant step size and random initialization instead. Additionally, our overall algorithm achieves nearly linear sample complexity, $\mathcal{O}(d \, \mathrm{polylog}(d))$.

LEARN: An Invex Loss for Outlier Oblivious Robust Online Optimization

We study a robust online convex optimization framework, where an adversary can introduce outliers by corrupting loss functions in an arbitrary number of rounds k, unknown to the learner. Our focus is on a novel setting allowing unbounded domains and large gradients for the losses without relying on a Lipschitz assumption. We introduce the Log Exponential Adjusted Robust and iNvex (LEARN) loss, a non-convex (invex) robust loss function to mitigate the effects of outliers and develop a robust variant of the online gradient descent algorithm by leveraging the LEARN loss. We establish tight regret guarantees (up to constants), in a dynamic setting, with respect to the uncorrupted rounds and conduct experiments to validate our theory. Furthermore, we present a unified analysis framework for developing online optimization algorithms for non-convex (invex) losses, utilizing it to provide regret bounds with respect to the LEARN loss, which may be of independent interest.

Invex Programs: First Order Algorithms and Their Convergence

Invex programs are a special kind of non-convex problems which attain global minima at every stationary point. While classical first-order gradient descent methods can solve them, they converge very slowly. In this paper, we propose new first-order algorithms to solve the general class of invex problems. We identify sufficient conditions for convergence of our algorithms and provide rates of convergence. Furthermore, we go beyond unconstrained problems and provide a novel projected gradient method for constrained invex programs with convergence rate guarantees. We compare and contrast our results with existing first-order algorithms for a variety of unconstrained and constrained invex problems. To the best of our knowledge, our proposed algorithm is the first algorithm to solve constrained invex programs.

Outlier-robust Estimation of a Sparse Linear Model Using Invexity

In this paper, we study problem of estimating a sparse regression vector with correct support in the presence of outlier samples. The inconsistency of lasso-type methods is well known in this scenario. We propose a combinatorial version of outlier-robust lasso which also identifies clean samples. Subsequently, we use these clean samples to make a good estimation. We also provide a novel invex relaxation for the combinatorial problem and provide provable theoretical guarantees for this relaxation. Finally, we conduct experiments to validate our theory and compare our results against standard lasso.

A Novel Plug-and-Play Approach for Adversarially Robust Generalization

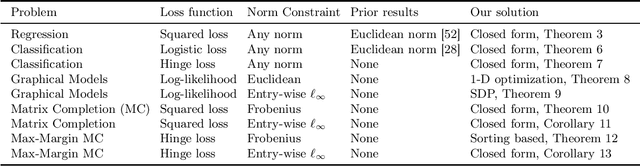
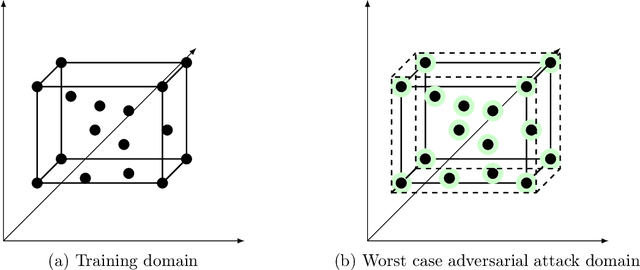
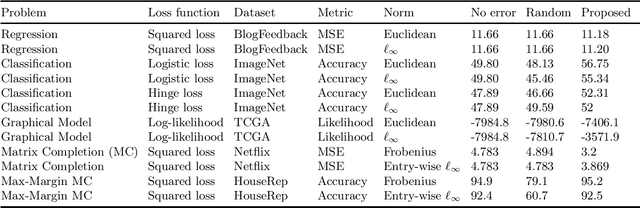
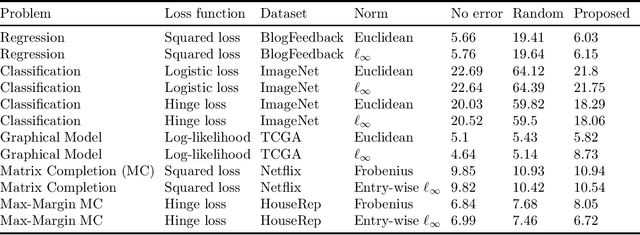
In this work, we propose a robust framework that employs adversarially robust training to safeguard the machine learning models against perturbed testing data. We achieve this by incorporating the worst-case additive adversarial error within a fixed budget for each sample during model estimation. Our main focus is to provide a plug-and-play solution that can be incorporated in the existing machine learning algorithms with minimal changes. To that end, we derive the closed-form ready-to-use solution for several widely used loss functions with a variety of norm constraints on adversarial perturbation. Finally, we validate our approach by showing significant performance improvement on real-world datasets for supervised problems such as regression and classification, as well as for unsupervised problems such as matrix completion and learning graphical models, with very little computational overhead.

Sparse Mixed Linear Regression with Guarantees: Taming an Intractable Problem with Invex Relaxation

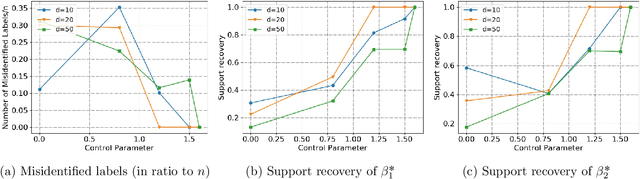
In this paper, we study the problem of sparse mixed linear regression on an unlabeled dataset that is generated from linear measurements from two different regression parameter vectors. Since the data is unlabeled, our task is not only to figure out a good approximation of the regression parameter vectors but also to label the dataset correctly. In its original form, this problem is NP-hard. The most popular algorithms to solve this problem (such as Expectation-Maximization) have a tendency to stuck at local minima. We provide a novel invex relaxation for this intractable problem which leads to a solution with provable theoretical guarantees. This relaxation enables exact recovery of data labels. Furthermore, we recover a close approximation of the regression parameter vectors which match the true parameter vectors in support and sign. Our formulation uses a carefully constructed primal dual witnesses framework for the invex problem. Furthermore, we show that the sample complexity of our method is only logarithmic in terms of the dimension of the regression parameter vectors.

Information-Theoretic Bounds for Integral Estimation

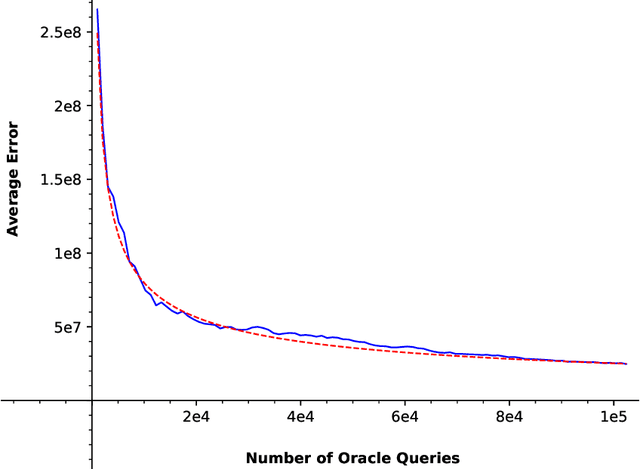
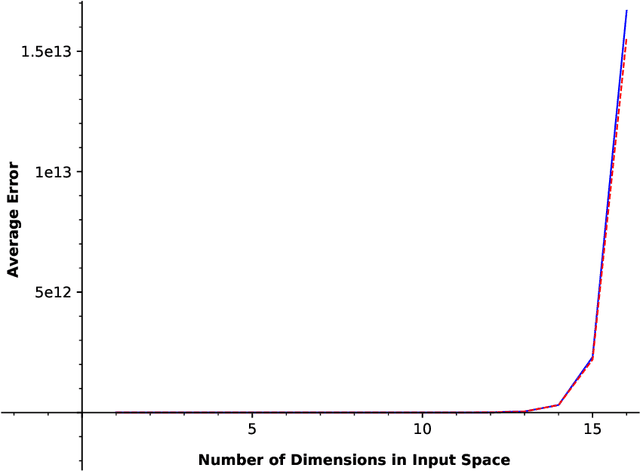
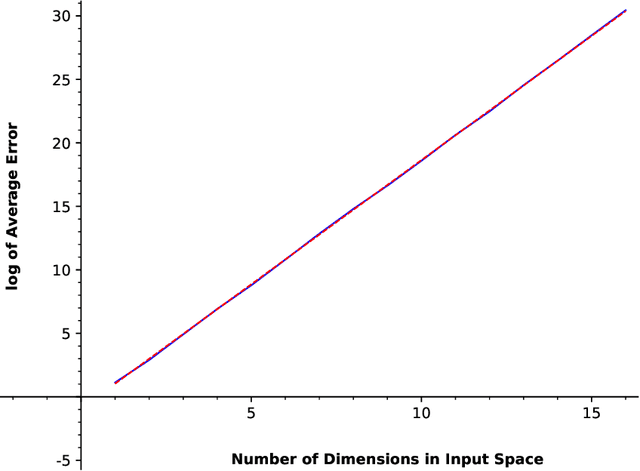
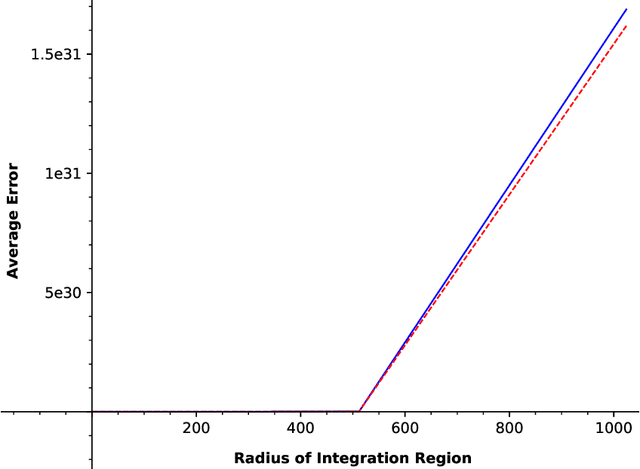
In this paper, we consider a zero-order stochastic oracle model of estimating definite integrals. In this model, integral estimation methods may query an oracle function for a fixed number of noisy values of the integrand function and use these values to produce an estimate of the integral. We first show that the information-theoretic error lower bound for estimating the integral of a $d$-dimensional function over a region with $l_\infty$ radius $r$ using at most $T$ queries to the oracle function is $\Omega(2^d r^{d+1}\sqrt{d/T})$. Additionally, we find that the Gaussian Quadrature method under the same model achieves a rate of $O(2^{d}r^d/\sqrt{T})$ for functions with zero fourth and higher-order derivatives with respect to individual dimensions, and for Gaussian oracles, this rate is tight. For functions with nonzero fourth derivatives, the Gaussian Quadrature method achieves an upper bound which is not tight with the information-theoretic lower bound. Therefore, it is not minimax optimal, so there is space for the development of better integral estimation methods for such functions.

Fair Sparse Regression with Clustering: An Invex Relaxation for a Combinatorial Problem

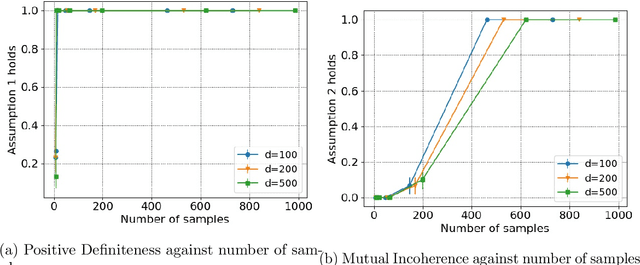
In this paper, we study the problem of fair sparse regression on a biased dataset where bias depends upon a hidden binary attribute. The presence of a hidden attribute adds an extra layer of complexity to the problem by combining sparse regression and clustering with unknown binary labels. The corresponding optimization problem is combinatorial but we propose a novel relaxation of it as an \emph{invex} optimization problem. To the best of our knowledge, this is the first invex relaxation for a combinatorial problem. We show that the inclusion of the debiasing/fairness constraint in our model has no adverse effect on the performance. Rather, it enables the recovery of the hidden attribute. The support of our recovered regression parameter vector matches exactly with the true parameter vector. Moreover, we simultaneously solve the clustering problem by recovering the exact value of the hidden attribute for each sample. Our method uses carefully constructed primal dual witnesses to solve the combinatorial problem. We provide theoretical guarantees which hold as long as the number of samples is polynomial in terms of the dimension of the regression parameter vector.

A Simple Unified Framework for High Dimensional Bandit Problems

Stochastic high dimensional bandit problems with low dimensional structure are useful in different applications such as online advertising and drug discovery. In this work, we propose a simple unified algorithm for such problems and present a general analysis framework for the regret upper bound of our algorithm. We show that under some mild unified assumptions, our algorithm can be applied to different high dimensional bandit problems. Our framework utilizes the low dimensional structure to guide the parameter estimation in the problem, therefore our algorithm achieves the best regret bounds in the LASSO bandit, better bounds in the low-rank matrix bandit and the group sparse matrix bandit, as well as a novel bound in the multi-agent LASSO bandit.