Jean Honorio
Stony Brook University
Personalized Federated X -armed Bandit
Oct 25, 2023Abstract:In this work, we study the personalized federated $\mathcal{X}$-armed bandit problem, where the heterogeneous local objectives of the clients are optimized simultaneously in the federated learning paradigm. We propose the \texttt{PF-PNE} algorithm with a unique double elimination strategy, which safely eliminates the non-optimal regions while encouraging federated collaboration through biased but effective evaluations of the local objectives. The proposed \texttt{PF-PNE} algorithm is able to optimize local objectives with arbitrary levels of heterogeneity, and its limited communications protects the confidentiality of the client-wise reward data. Our theoretical analysis shows the benefit of the proposed algorithm over single-client algorithms. Experimentally, \texttt{PF-PNE} outperforms multiple baselines on both synthetic and real life datasets.
Invex Programs: First Order Algorithms and Their Convergence
Jul 10, 2023Abstract:Invex programs are a special kind of non-convex problems which attain global minima at every stationary point. While classical first-order gradient descent methods can solve them, they converge very slowly. In this paper, we propose new first-order algorithms to solve the general class of invex problems. We identify sufficient conditions for convergence of our algorithms and provide rates of convergence. Furthermore, we go beyond unconstrained problems and provide a novel projected gradient method for constrained invex programs with convergence rate guarantees. We compare and contrast our results with existing first-order algorithms for a variety of unconstrained and constrained invex problems. To the best of our knowledge, our proposed algorithm is the first algorithm to solve constrained invex programs.
Outlier-robust Estimation of a Sparse Linear Model Using Invexity
Jun 22, 2023Abstract:In this paper, we study problem of estimating a sparse regression vector with correct support in the presence of outlier samples. The inconsistency of lasso-type methods is well known in this scenario. We propose a combinatorial version of outlier-robust lasso which also identifies clean samples. Subsequently, we use these clean samples to make a good estimation. We also provide a novel invex relaxation for the combinatorial problem and provide provable theoretical guarantees for this relaxation. Finally, we conduct experiments to validate our theory and compare our results against standard lasso.
Partial Inference in Structured Prediction
Jun 06, 2023Abstract:In this paper, we examine the problem of partial inference in the context of structured prediction. Using a generative model approach, we consider the task of maximizing a score function with unary and pairwise potentials in the space of labels on graphs. Employing a two-stage convex optimization algorithm for label recovery, we analyze the conditions under which a majority of the labels can be recovered. We introduce a novel perspective on the Karush-Kuhn-Tucker (KKT) conditions and primal and dual construction, and provide statistical and topological requirements for partial recovery with provable guarantees.
Matrix Completion from General Deterministic Sampling Patterns
Jun 04, 2023Abstract:Most of the existing works on provable guarantees for low-rank matrix completion algorithms rely on some unrealistic assumptions such that matrix entries are sampled randomly or the sampling pattern has a specific structure. In this work, we establish theoretical guarantee for the exact and approximate low-rank matrix completion problems which can be applied to any deterministic sampling schemes. For this, we introduce a graph having observed entries as its edge set, and investigate its graph properties involving the performance of the standard constrained nuclear norm minimization algorithm. We theoretically and experimentally show that the algorithm can be successful as the observation graph is well-connected and has similar node degrees. Our result can be viewed as an extension of the works by Bhojanapalli and Jain [2014] and Burnwal and Vidyasagar [2020], in which the node degrees of the observation graph were assumed to be the same. In particular, our theory significantly improves their results when the underlying matrix is symmetric.
PyXAB -- A Python Library for $\mathcal{X}$-Armed Bandit and Online Blackbox Optimization Algorithms
Mar 07, 2023Abstract:We introduce a Python open-source library for $\mathcal{X}$-armed bandit and online blackbox optimization named PyXAB. PyXAB contains the implementations for more than 10 $\mathcal{X}$-armed bandit algorithms, such as HOO, StoSOO, HCT, and the most recent works GPO and VHCT. PyXAB also provides the most commonly-used synthetic objectives to evaluate the performance of different algorithms and the various choices of the hierarchical partitions on the parameter space. The online documentation for PyXAB includes clear instructions for installation, straight-forward examples, detailed feature descriptions, and a complete reference of the API. PyXAB is released under the MIT license in order to encourage both academic and industrial usage. The library can be directly installed from PyPI with its source code available at https://github.com/WilliamLwj/PyXAB
Exact Inference in High-order Structured Prediction
Feb 07, 2023Abstract:In this paper, we study the problem of inference in high-order structured prediction tasks. In the context of Markov random fields, the goal of a high-order inference task is to maximize a score function on the space of labels, and the score function can be decomposed into sum of unary and high-order potentials. We apply a generative model approach to study the problem of high-order inference, and provide a two-stage convex optimization algorithm for exact label recovery. We also provide a new class of hypergraph structural properties related to hyperedge expansion that drives the success in general high-order inference problems. Finally, we connect the performance of our algorithm and the hyperedge expansion property using a novel hypergraph Cheeger-type inequality.
Support Recovery in Sparse PCA with Non-Random Missing Data
Feb 03, 2023Abstract:We analyze a practical algorithm for sparse PCA on incomplete and noisy data under a general non-random sampling scheme. The algorithm is based on a semidefinite relaxation of the $\ell_1$-regularized PCA problem. We provide theoretical justification that under certain conditions, we can recover the support of the sparse leading eigenvector with high probability by obtaining a unique solution. The conditions involve the spectral gap between the largest and second-largest eigenvalues of the true data matrix, the magnitude of the noise, and the structural properties of the observed entries. The concepts of algebraic connectivity and irregularity are used to describe the structural properties of the observed entries. We empirically justify our theorem with synthetic and real data analysis. We also show that our algorithm outperforms several other sparse PCA approaches especially when the observed entries have good structural properties. As a by-product of our analysis, we provide two theorems to handle a deterministic sampling scheme, which can be applied to other matrix-related problems.
Learning Against Distributional Uncertainty: On the Trade-off Between Robustness and Specificity
Jan 31, 2023Abstract:Trustworthy machine learning aims at combating distributional uncertainties in training data distributions compared to population distributions. Typical treatment frameworks include the Bayesian approach, (min-max) distributionally robust optimization (DRO), and regularization. However, two issues have to be raised: 1) All these methods are biased estimators of the true optimal cost; 2) the prior distribution in the Bayesian method, the radius of the distributional ball in the DRO method, and the regularizer in the regularization method are difficult to specify. This paper studies a new framework that unifies the three approaches and that addresses the two challenges mentioned above. The asymptotic properties (e.g., consistency and asymptotic normalities), non-asymptotic properties (e.g., unbiasedness and generalization error bound), and a Monte--Carlo-based solution method of the proposed model are studied. The new model reveals the trade-off between the robustness to the unseen data and the specificity to the training data.
A Theoretical Study of The Effects of Adversarial Attacks on Sparse Regression
Dec 22, 2022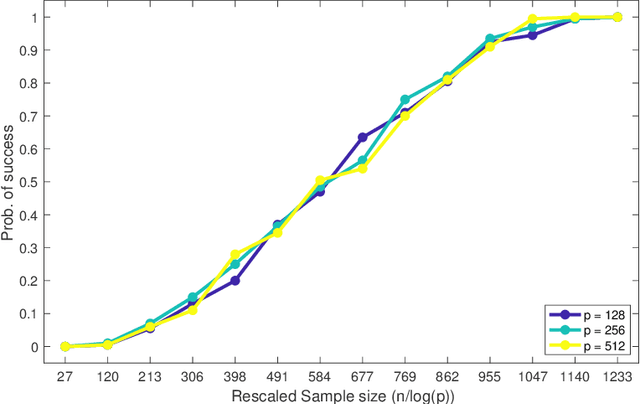
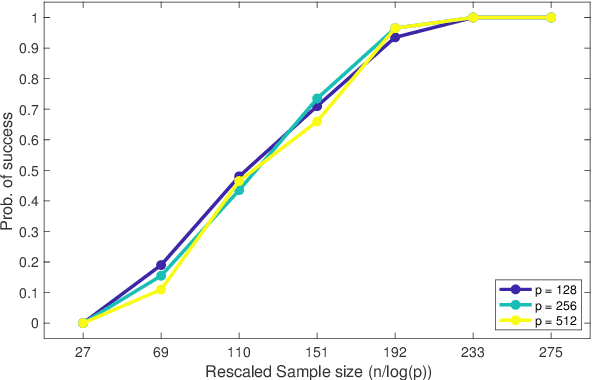

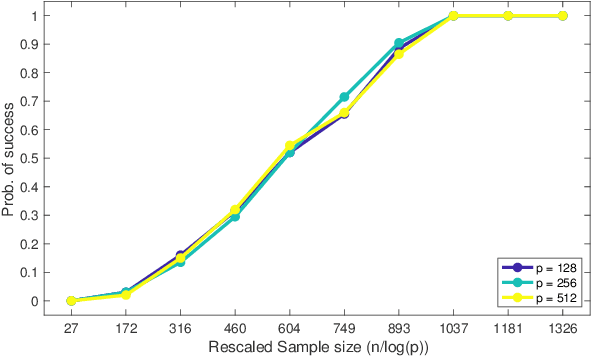
Abstract:This paper analyzes $\ell_1$ regularized linear regression under the challenging scenario of having only adversarially corrupted data for training. We use the primal-dual witness paradigm to provide provable performance guarantees for the support of the estimated regression parameter vector to match the actual parameter. Our theoretical analysis shows the counter-intuitive result that an adversary can influence sample complexity by corrupting the irrelevant features, i.e., those corresponding to zero coefficients of the regression parameter vector, which, consequently, do not affect the dependent variable. As any adversarially robust algorithm has its limitations, our theoretical analysis identifies the regimes under which the learning algorithm and adversary can dominate over each other. It helps us to analyze these fundamental limits and address critical scientific questions of which parameters (like mutual incoherence, the maximum and minimum eigenvalue of the covariance matrix, and the budget of adversarial perturbation) play a role in the high or low probability of success of the LASSO algorithm. Also, the derived sample complexity is logarithmic with respect to the size of the regression parameter vector, and our theoretical claims are validated by empirical analysis on synthetic and real-world datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge