A Theoretical Study of The Effects of Adversarial Attacks on Sparse Regression

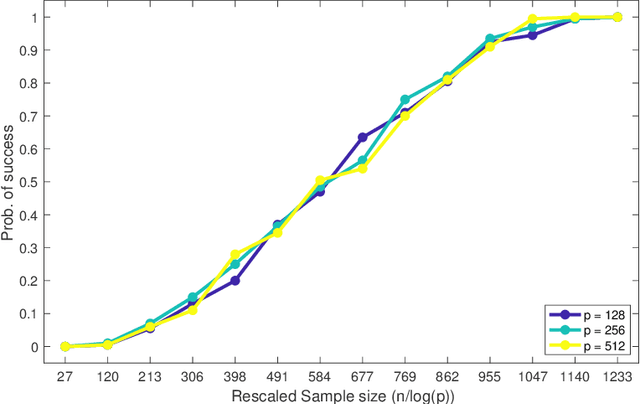
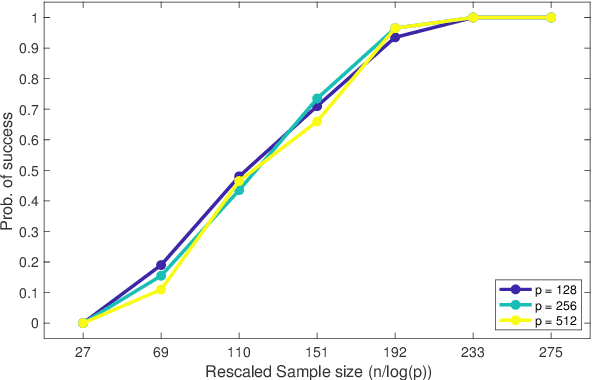
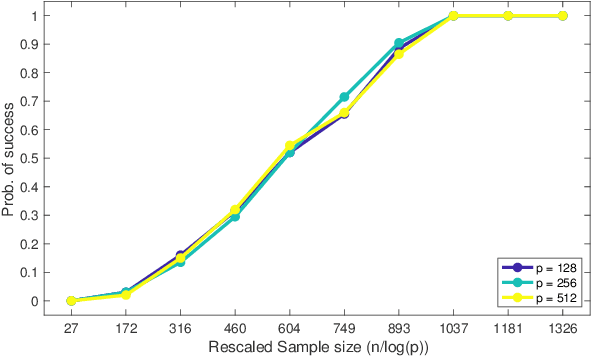
This paper analyzes $\ell_1$ regularized linear regression under the challenging scenario of having only adversarially corrupted data for training. We use the primal-dual witness paradigm to provide provable performance guarantees for the support of the estimated regression parameter vector to match the actual parameter. Our theoretical analysis shows the counter-intuitive result that an adversary can influence sample complexity by corrupting the irrelevant features, i.e., those corresponding to zero coefficients of the regression parameter vector, which, consequently, do not affect the dependent variable. As any adversarially robust algorithm has its limitations, our theoretical analysis identifies the regimes under which the learning algorithm and adversary can dominate over each other. It helps us to analyze these fundamental limits and address critical scientific questions of which parameters (like mutual incoherence, the maximum and minimum eigenvalue of the covariance matrix, and the budget of adversarial perturbation) play a role in the high or low probability of success of the LASSO algorithm. Also, the derived sample complexity is logarithmic with respect to the size of the regression parameter vector, and our theoretical claims are validated by empirical analysis on synthetic and real-world datasets.

A Novel Plug-and-Play Approach for Adversarially Robust Generalization

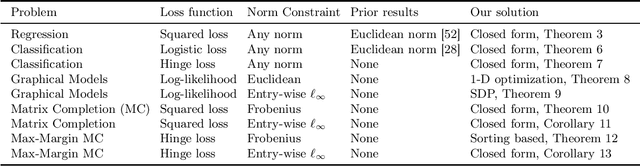
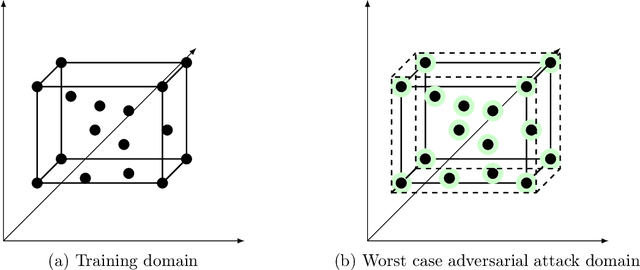
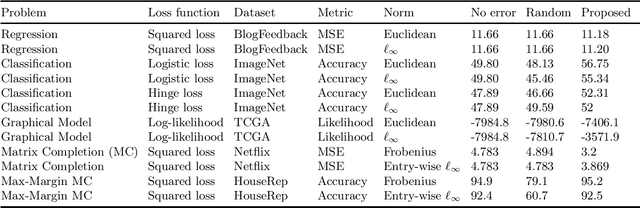
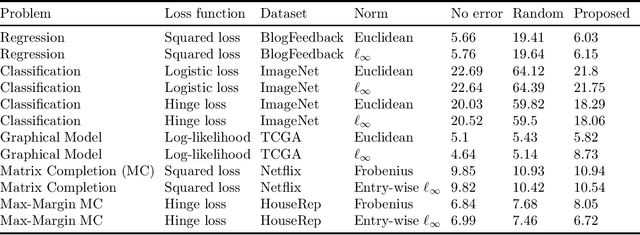
In this work, we propose a robust framework that employs adversarially robust training to safeguard the machine learning models against perturbed testing data. We achieve this by incorporating the worst-case additive adversarial error within a fixed budget for each sample during model estimation. Our main focus is to provide a plug-and-play solution that can be incorporated in the existing machine learning algorithms with minimal changes. To that end, we derive the closed-form ready-to-use solution for several widely used loss functions with a variety of norm constraints on adversarial perturbation. Finally, we validate our approach by showing significant performance improvement on real-world datasets for supervised problems such as regression and classification, as well as for unsupervised problems such as matrix completion and learning graphical models, with very little computational overhead.

Hyperedge Prediction using Tensor Eigenvalue Decomposition

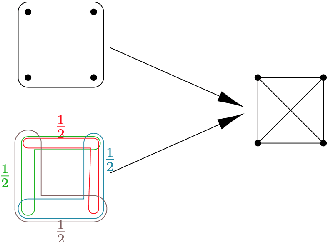
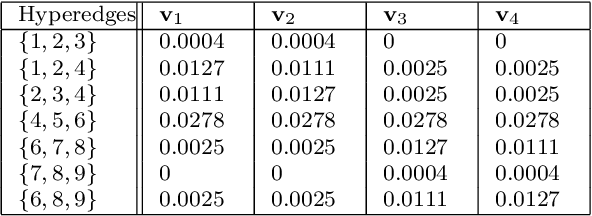
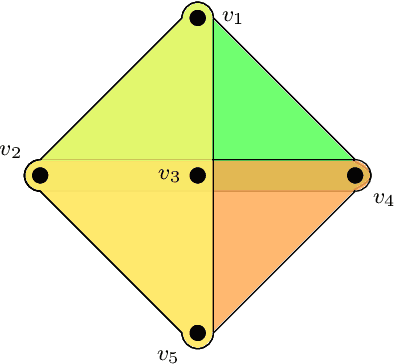
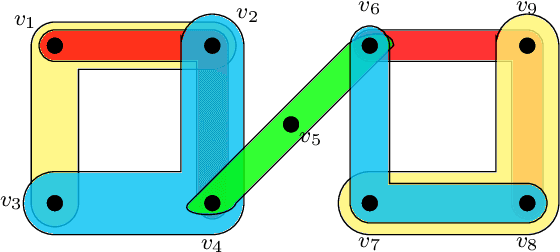
Link prediction in graphs is studied by modeling the dyadic interactions among two nodes. The relationships can be more complex than simple dyadic interactions and could require the user to model super-dyadic associations among nodes. Such interactions can be modeled using a hypergraph, which is a generalization of a graph where a hyperedge can connect more than two nodes. In this work, we consider the problem of hyperedge prediction in a $k-$uniform hypergraph. We utilize the tensor-based representation of hypergraphs and propose a novel interpretation of the tensor eigenvectors. This is further used to propose a hyperedge prediction algorithm. The proposed algorithm utilizes the \textit{Fiedler} eigenvector computed using tensor eigenvalue decomposition of hypergraph Laplacian. The \textit{Fiedler} eigenvector is used to evaluate the construction cost of new hyperedges, which is further utilized to determine the most probable hyperedges to be constructed. The functioning and efficacy of the proposed method are illustrated using some example hypergraphs and a few real datasets. The code for the proposed method is available on https://github.com/d-maurya/hypred_ tensorEVD

Identification of Errors-in-Variables ARX Models Using Modified Dynamic Iterative PCA

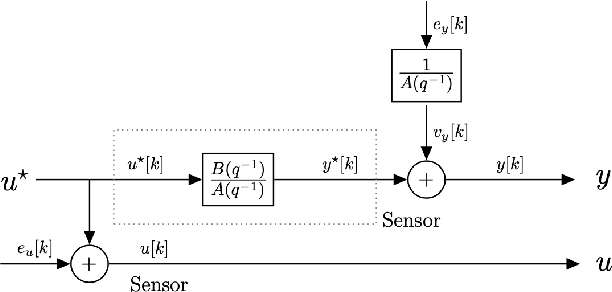
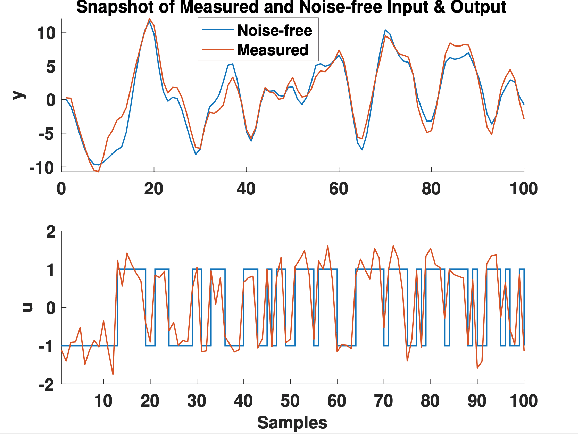
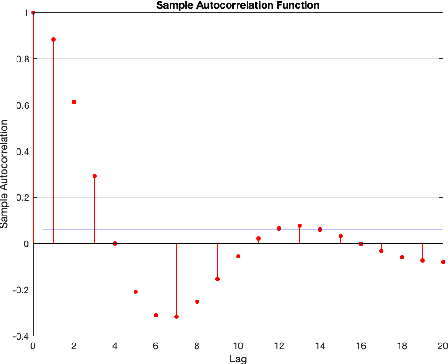
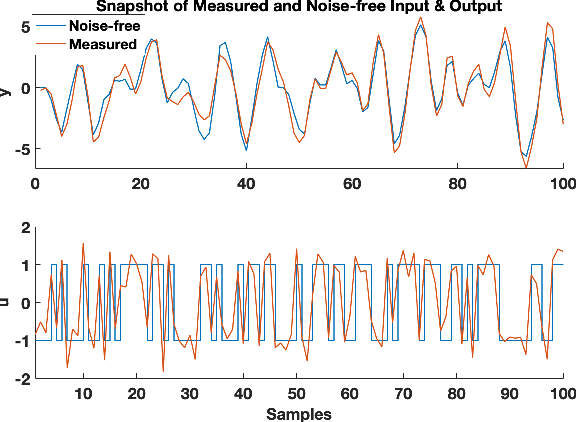
Identification of autoregressive models with exogenous input (ARX) is a classical problem in system identification. This article considers the errors-in-variables (EIV) ARX model identification problem, where input measurements are also corrupted with noise. The recently proposed DIPCA technique solves the EIV identification problem but is only applicable to white measurement errors. We propose a novel identification algorithm based on a modified Dynamic Iterative Principal Components Analysis (DIPCA) approach for identifying the EIV-ARX model for single-input, single-output (SISO) systems where the output measurements are corrupted with coloured noise consistent with the ARX model. Most of the existing methods assume important parameters like input-output orders, delay, or noise-variances to be known. This work's novelty lies in the joint estimation of error variances, process order, delay, and model parameters. The central idea used to obtain all these parameters in a theoretically rigorous manner is based on transforming the lagged measurements using the appropriate error covariance matrix, which is obtained using estimated error variances and model parameters. Simulation studies on two systems are presented to demonstrate the efficacy of the proposed algorithm.

Hypergraph Partitioning using Tensor Eigenvalue Decomposition

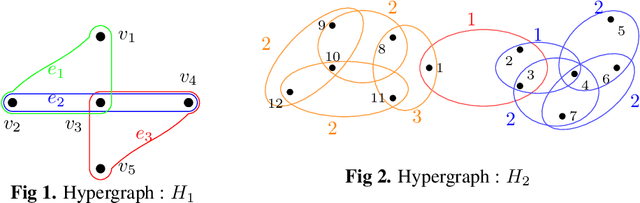
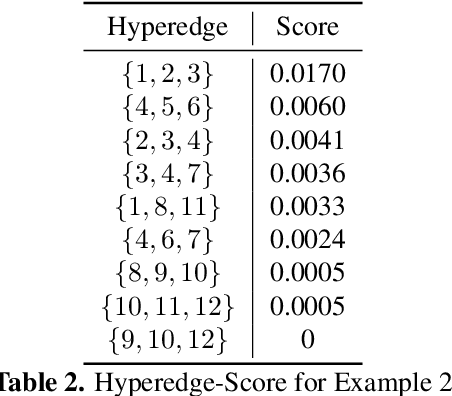
Hypergraphs have gained increasing attention in the machine learning community lately due to their superiority over graphs in capturing super-dyadic interactions among entities. In this work, we propose a novel approach for the partitioning of k-uniform hypergraphs. Most of the existing methods work by reducing the hypergraph to a graph followed by applying standard graph partitioning algorithms. The reduction step restricts the algorithms to capturing only some weighted pairwise interactions and hence loses essential information about the original hypergraph. We overcome this issue by utilizing the tensor-based representation of hypergraphs, which enables us to capture actual super-dyadic interactions. We prove that the hypergraph to graph reduction is a special case of tensor contraction. We extend the notion of minimum ratio-cut and normalized-cut from graphs to hypergraphs and show the relaxed optimization problem is equivalent to tensor eigenvalue decomposition. This novel formulation also enables us to capture different ways of cutting a hyperedge, unlike the existing reduction approaches. We propose a hypergraph partitioning algorithm inspired from spectral graph theory that can accommodate this notion of hyperedge cuts. We also derive a tighter upper bound on the minimum positive eigenvalue of even-order hypergraph Laplacian tensor in terms of its conductance, which is utilized in the partitioning algorithm to approximate the normalized cut. The efficacy of the proposed method is demonstrated numerically on simple hypergraphs. We also show improvement for the min-cut solution on 2-uniform hypergraphs (graphs) over the standard spectral partitioning algorithm.

Incorporating prior knowledge about structural constraints in model identification

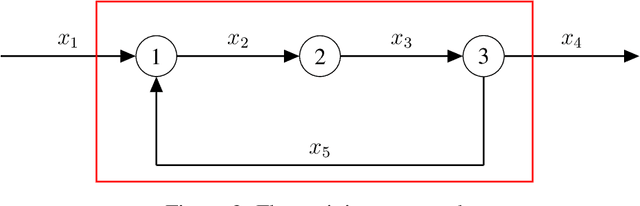
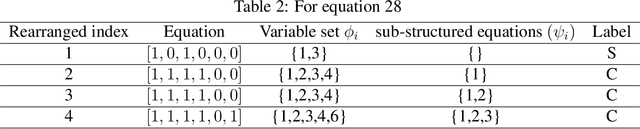
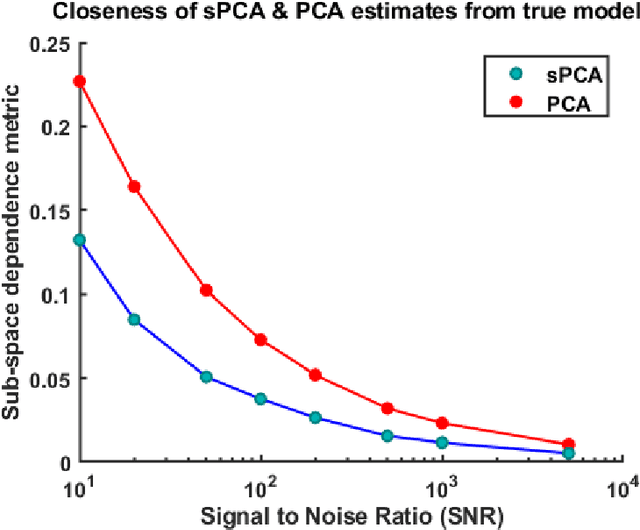
Model identification is a crucial problem in chemical industries. In recent years, there has been increasing interest in learning data-driven models utilizing partial knowledge about the system of interest. Most techniques for model identification do not provide the freedom to incorporate any partial information such as the structure of the model. In this article, we propose model identification techniques that could leverage such partial information to produce better estimates. Specifically, we propose Structural Principal Component Analysis (SPCA) which improvises over existing methods like PCA by utilizing the essential structural information about the model. Most of the existing methods or closely related methods use sparsity constraints which could be computationally expensive. Our proposed method is a wise modification of PCA to utilize structural information. The efficacy of the proposed approach is demonstrated using synthetic and industrial case-studies.