A Theoretical Study of The Effects of Adversarial Attacks on Sparse Regression
Paper and Code
Dec 22, 2022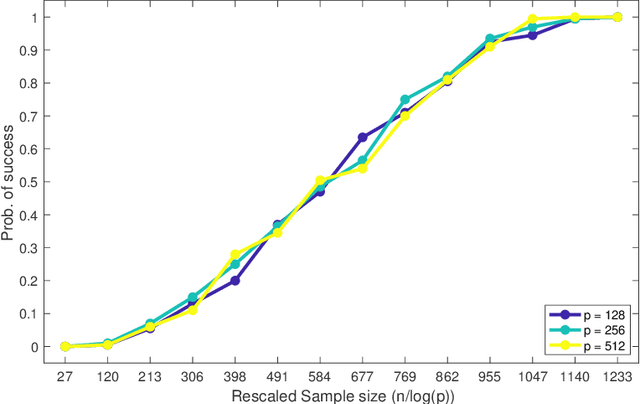
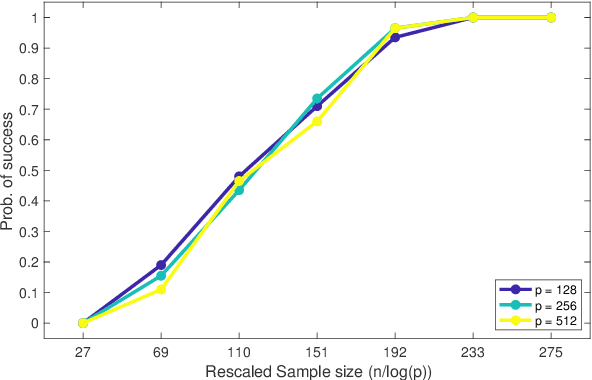

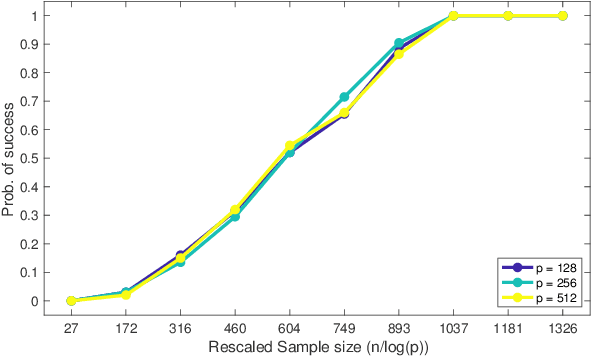
This paper analyzes $\ell_1$ regularized linear regression under the challenging scenario of having only adversarially corrupted data for training. We use the primal-dual witness paradigm to provide provable performance guarantees for the support of the estimated regression parameter vector to match the actual parameter. Our theoretical analysis shows the counter-intuitive result that an adversary can influence sample complexity by corrupting the irrelevant features, i.e., those corresponding to zero coefficients of the regression parameter vector, which, consequently, do not affect the dependent variable. As any adversarially robust algorithm has its limitations, our theoretical analysis identifies the regimes under which the learning algorithm and adversary can dominate over each other. It helps us to analyze these fundamental limits and address critical scientific questions of which parameters (like mutual incoherence, the maximum and minimum eigenvalue of the covariance matrix, and the budget of adversarial perturbation) play a role in the high or low probability of success of the LASSO algorithm. Also, the derived sample complexity is logarithmic with respect to the size of the regression parameter vector, and our theoretical claims are validated by empirical analysis on synthetic and real-world datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge