Hypergraph Partitioning using Tensor Eigenvalue Decomposition
Paper and Code
Nov 16, 2020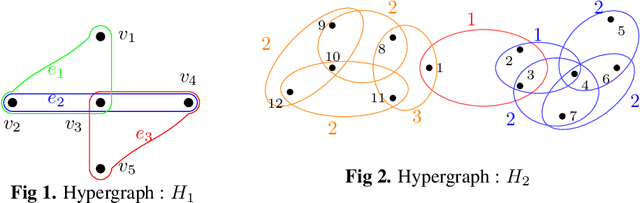
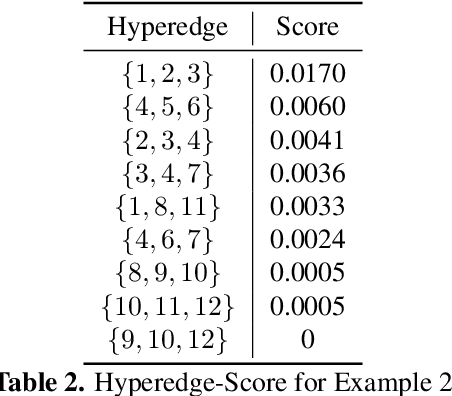
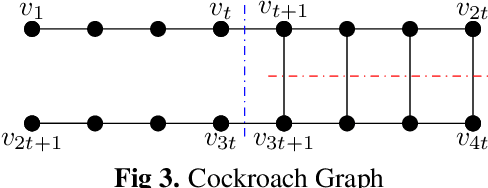

Hypergraphs have gained increasing attention in the machine learning community lately due to their superiority over graphs in capturing super-dyadic interactions among entities. In this work, we propose a novel approach for the partitioning of k-uniform hypergraphs. Most of the existing methods work by reducing the hypergraph to a graph followed by applying standard graph partitioning algorithms. The reduction step restricts the algorithms to capturing only some weighted pairwise interactions and hence loses essential information about the original hypergraph. We overcome this issue by utilizing the tensor-based representation of hypergraphs, which enables us to capture actual super-dyadic interactions. We prove that the hypergraph to graph reduction is a special case of tensor contraction. We extend the notion of minimum ratio-cut and normalized-cut from graphs to hypergraphs and show the relaxed optimization problem is equivalent to tensor eigenvalue decomposition. This novel formulation also enables us to capture different ways of cutting a hyperedge, unlike the existing reduction approaches. We propose a hypergraph partitioning algorithm inspired from spectral graph theory that can accommodate this notion of hyperedge cuts. We also derive a tighter upper bound on the minimum positive eigenvalue of even-order hypergraph Laplacian tensor in terms of its conductance, which is utilized in the partitioning algorithm to approximate the normalized cut. The efficacy of the proposed method is demonstrated numerically on simple hypergraphs. We also show improvement for the min-cut solution on 2-uniform hypergraphs (graphs) over the standard spectral partitioning algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge