Upstream flow geometries can be uniquely learnt from single-point turbulence signatures

We test the hypothesis that the microscopic temporal structure of near-field turbulence downstream of a sudden contraction contains geometry-identifiable information pertaining to the shape of the upstream obstruction. We measure a set of spatially sparse velocity time-series data downstream of differently-shaped orifices. We then train random forest multiclass classifier models on a vector of invariants derived from this time-series. We test the above hypothesis with 25 somewhat similar orifice shapes to push the model to its extreme limits. Remarkably, the algorithm was able to identify the orifice shape with 100% accuracy and 100% precision. This outcome is enabled by the uniqueness in the downstream temporal evolution of turbulence structures in the flow past orifices, combined with the random forests' ability to learn subtle yet discerning features in the turbulence microstructure. We are also able to explain the underlying flow physics that enables such classification by listing the invariant measures in the order of increasing information entropy. We show that the temporal autocorrelation coefficients of the time-series are most sensitive to orifice shape and are therefore informative. The ability to identify changes in system geometry without the need for physical disassembly offers tremendous potential for flow control and system identification. Furthermore, the proposed approach could potentially have significant applications in other unrelated fields as well, by deploying the core methodology of training random forest classifiers on vectors of invariant measures obtained from time-series data.

User authentication system based on human exhaled breath physics

This work, in a pioneering approach, attempts to build a biometric system that works purely based on the fluid mechanics governing exhaled breath. We test the hypothesis that the structure of turbulence in exhaled human breath can be exploited to build biometric algorithms. This work relies on the idea that the extrathoracic airway is unique for every individual, making the exhaled breath a biomarker. Methods including classical multi-dimensional hypothesis testing approach and machine learning models are employed in building user authentication algorithms, namely user confirmation and user identification. A user confirmation algorithm tries to verify whether a user is the person they claim to be. A user identification algorithm tries to identify a user's identity with no prior information available. A dataset of exhaled breath time series samples from 94 human subjects was used to evaluate the performance of these algorithms. The user confirmation algorithms performed exceedingly well for the given dataset with over $97\%$ true confirmation rate. The machine learning based algorithm achieved a good true confirmation rate, reiterating our understanding of why machine learning based algorithms typically outperform classical hypothesis test based algorithms. The user identification algorithm performs reasonably well with the provided dataset with over $50\%$ of the users identified as being within two possible suspects. We show surprisingly unique turbulent signatures in the exhaled breath that have not been discovered before. In addition to discussions on a novel biometric system, we make arguments to utilise this idea as a tool to gain insights into the morphometric variation of extrathoracic airway across individuals. Such tools are expected to have future potential in the area of personalised medicines.

CDiNN -Convex Difference Neural Networks

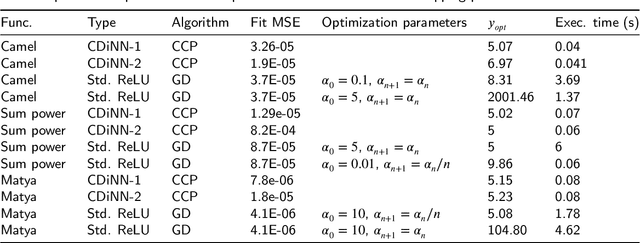
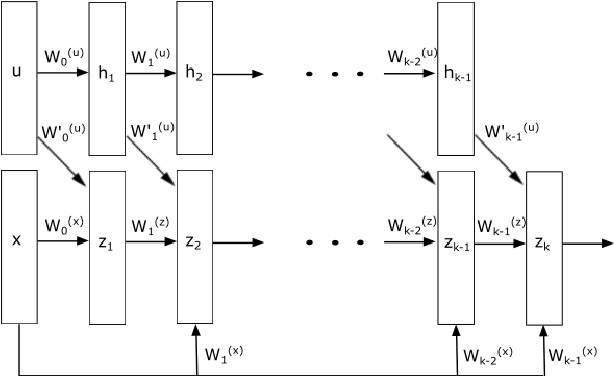
Neural networks with ReLU activation function have been shown to be universal function approximators and learn function mapping as non-smooth functions. Recently, there is considerable interest in the use of neural networks in applications such as optimal control. It is well-known that optimization involving non-convex, non-smooth functions are computationally intensive and have limited convergence guarantees. Moreover, the choice of optimization hyper-parameters used in gradient descent/ascent significantly affect the quality of the obtained solutions. A new neural network architecture called the Input Convex Neural Networks (ICNNs) learn the output as a convex function of inputs thereby allowing the use of efficient convex optimization methods. Use of ICNNs for determining the input for minimizing output has two major problems: learning of a non-convex function as a convex mapping could result in significant function approximation error, and we also note that the existing representations cannot capture simple dynamic structures like linear time delay systems. We attempt to address the above problems by introduction of a new neural network architecture, which we call the CDiNN, which learns the function as a difference of polyhedral convex functions from data. We also discuss that, in some cases, the optimal input can be obtained from CDiNN through difference of convex optimization with convergence guarantees and that at each iteration, the problem is reduced to a linear programming problem.

Incorporating prior knowledge about structural constraints in model identification

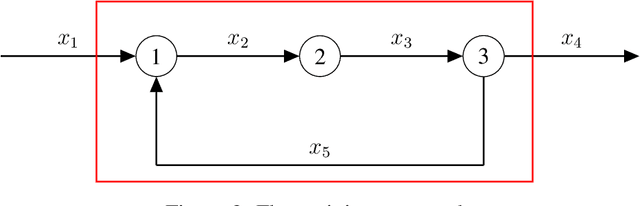
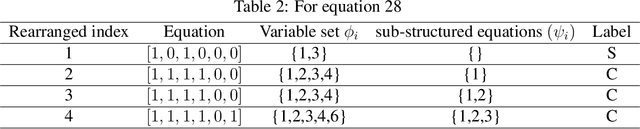
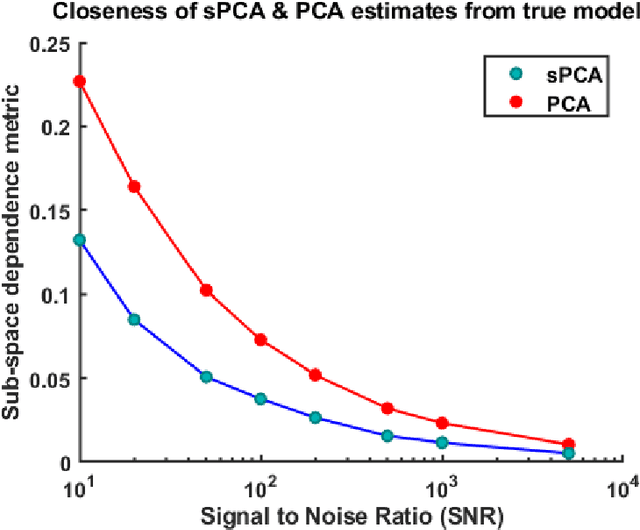
Model identification is a crucial problem in chemical industries. In recent years, there has been increasing interest in learning data-driven models utilizing partial knowledge about the system of interest. Most techniques for model identification do not provide the freedom to incorporate any partial information such as the structure of the model. In this article, we propose model identification techniques that could leverage such partial information to produce better estimates. Specifically, we propose Structural Principal Component Analysis (SPCA) which improvises over existing methods like PCA by utilizing the essential structural information about the model. Most of the existing methods or closely related methods use sparsity constraints which could be computationally expensive. Our proposed method is a wise modification of PCA to utilize structural information. The efficacy of the proposed approach is demonstrated using synthetic and industrial case-studies.