Identification of Errors-in-Variables ARX Models Using Modified Dynamic Iterative PCA

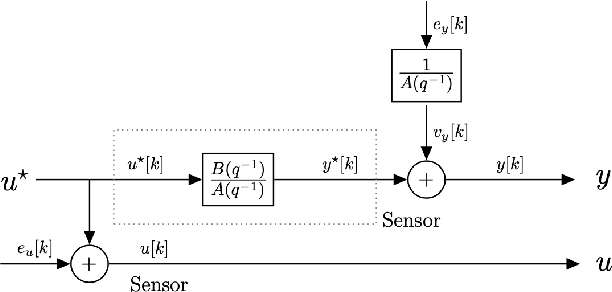
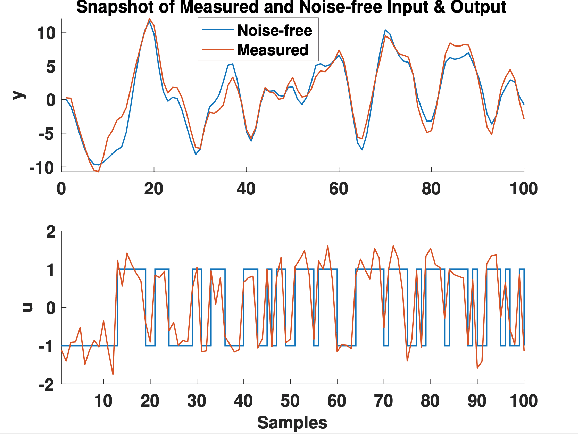
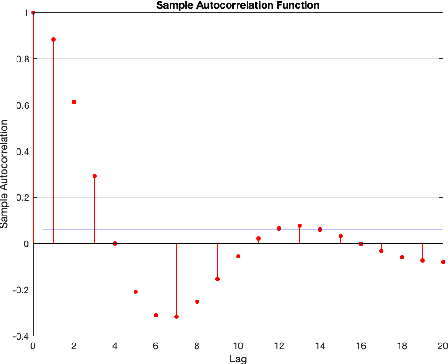
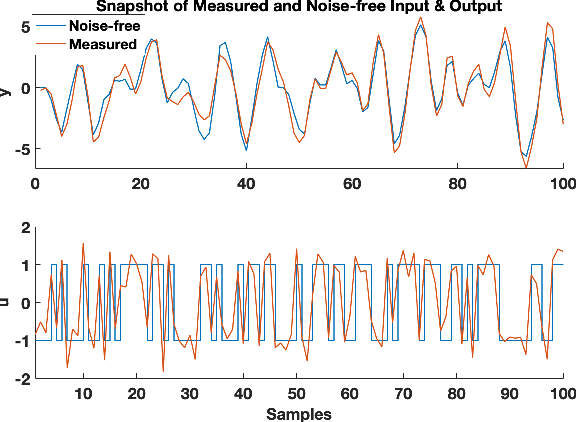
Identification of autoregressive models with exogenous input (ARX) is a classical problem in system identification. This article considers the errors-in-variables (EIV) ARX model identification problem, where input measurements are also corrupted with noise. The recently proposed DIPCA technique solves the EIV identification problem but is only applicable to white measurement errors. We propose a novel identification algorithm based on a modified Dynamic Iterative Principal Components Analysis (DIPCA) approach for identifying the EIV-ARX model for single-input, single-output (SISO) systems where the output measurements are corrupted with coloured noise consistent with the ARX model. Most of the existing methods assume important parameters like input-output orders, delay, or noise-variances to be known. This work's novelty lies in the joint estimation of error variances, process order, delay, and model parameters. The central idea used to obtain all these parameters in a theoretically rigorous manner is based on transforming the lagged measurements using the appropriate error covariance matrix, which is obtained using estimated error variances and model parameters. Simulation studies on two systems are presented to demonstrate the efficacy of the proposed algorithm.

Learning Conserved Networks from Flows

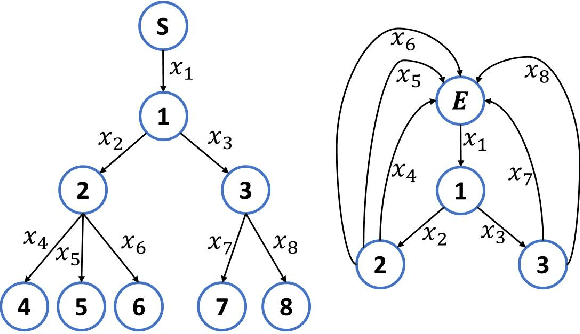
The network reconstruction problem is one of the challenging problems in network science. This work deals with reconstructing networks in which the flows are conserved around the nodes. These networks are referred to as conserved networks. We propose a novel concept of conservation graph for describing conserved networks. The properties of conservation graph are investigated. We develop a methodology to reconstruct conserved networks from flows by combining these graph properties with learning techniques, with polynomial time complexity. We show that exact network reconstruction is possible for radial networks. Further, we extend the methodology for reconstructing networks from noisy data. We demonstrate the proposed methods on different types of radial networks.

Network Topology Identification using PCA and its Graph Theoretic Interpretations

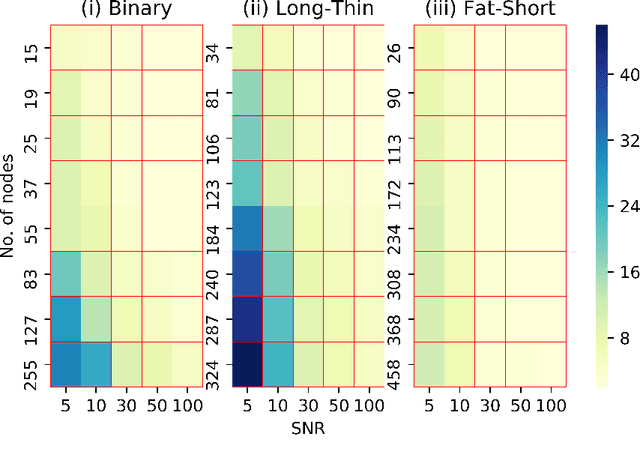
We solve the problem of identifying (reconstructing) network topology from steady state network measurements. Concretely, given only a data matrix $\mathbf{X}$ where the $X_{ij}$ entry corresponds to flow in edge $i$ in configuration (steady-state) $j$, we wish to find a network structure for which flow conservation is obeyed at all the nodes. This models many network problems involving conserved quantities like water, power, and metabolic networks. We show that identification is equivalent to learning a model $\mathbf{A_n}$ which captures the approximate linear relationships between the different variables comprising $\mathbf{X}$ (i.e. of the form $\mathbf{A_n X \approx 0}$) such that $\mathbf{A_n}$ is full rank (highest possible) and consistent with a network node-edge incidence structure. The problem is solved through a sequence of steps like estimating approximate linear relationships using Principal Component Analysis, obtaining f-cut-sets from these approximate relationships, and graph realization from f-cut-sets (or equivalently f-circuits). Each step and the overall process is polynomial time. The method is illustrated by identifying topology of a water distribution network. We also study the extent of identifiability from steady-state data.

Deconstructing Principal Component Analysis Using a Data Reconciliation Perspective

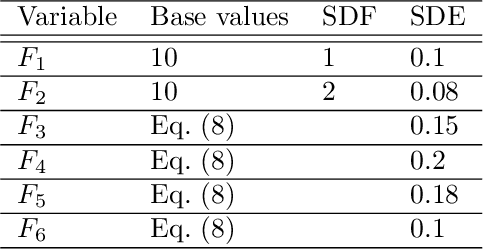
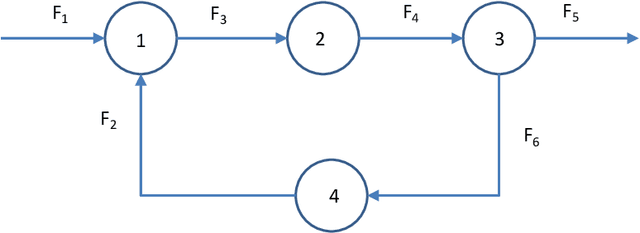
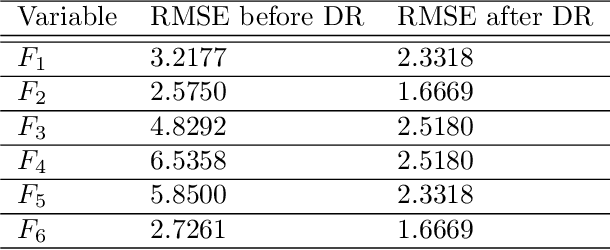
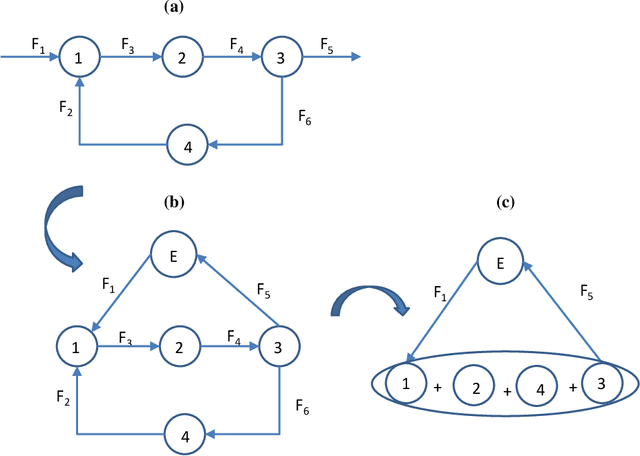
Data reconciliation (DR) and Principal Component Analysis (PCA) are two popular data analysis techniques in process industries. Data reconciliation is used to obtain accurate and consistent estimates of variables and parameters from erroneous measurements. PCA is primarily used as a method for reducing the dimensionality of high dimensional data and as a preprocessing technique for denoising measurements. These techniques have been developed and deployed independently of each other. The primary purpose of this article is to elucidate the close relationship between these two seemingly disparate techniques. This leads to a unified framework for applying PCA and DR. Further, we show how the two techniques can be deployed together in a collaborative and consistent manner to process data. The framework has been extended to deal with partially measured systems and to incorporate partial knowledge available about the process model.