Learning Conserved Networks from Flows

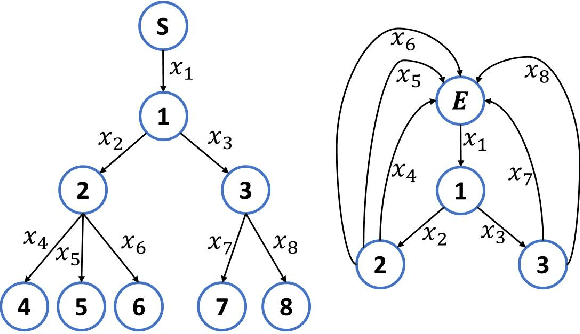
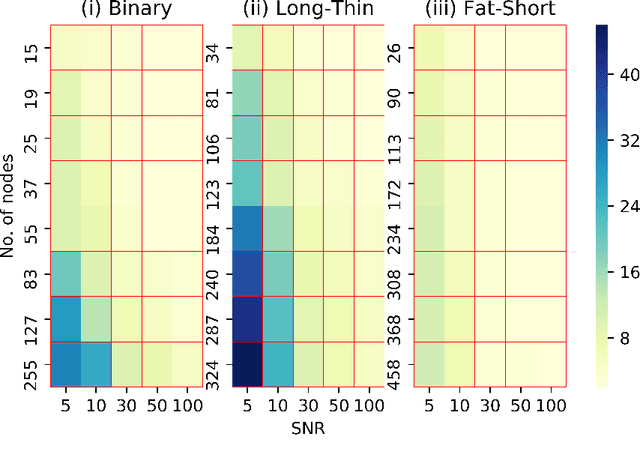
The network reconstruction problem is one of the challenging problems in network science. This work deals with reconstructing networks in which the flows are conserved around the nodes. These networks are referred to as conserved networks. We propose a novel concept of conservation graph for describing conserved networks. The properties of conservation graph are investigated. We develop a methodology to reconstruct conserved networks from flows by combining these graph properties with learning techniques, with polynomial time complexity. We show that exact network reconstruction is possible for radial networks. Further, we extend the methodology for reconstructing networks from noisy data. We demonstrate the proposed methods on different types of radial networks.

Identifying Topology of Power Distribution Networks Based on Smart Meter Data

In a power distribution network, the network topology information is essential for an efficient operation of the network. This information of network connectivity is not accurately available, at the low voltage level, due to uninformed changes that happen from time to time. In this paper, we propose a novel data--driven approach to identify the underlying network topology including the load phase connectivity from time series of energy measurements. The proposed method involves the application of Principal Component Analysis (PCA) and its graph-theoretic interpretation to infer the topology from smart meter energy measurements. The method is demonstrated through simulation on randomly generated networks and also on IEEE recognized Roy Billinton distribution test system.

Deconstructing Principal Component Analysis Using a Data Reconciliation Perspective

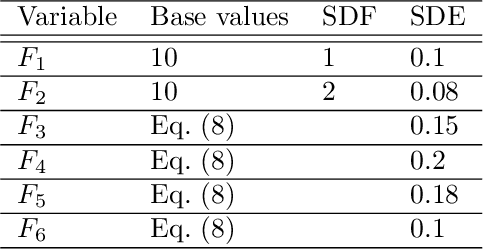
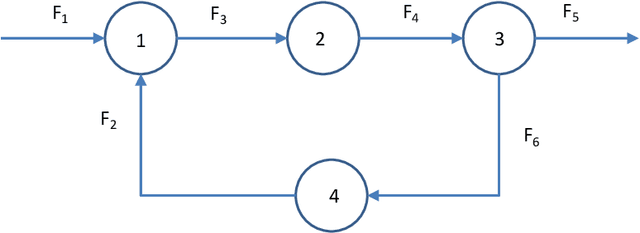
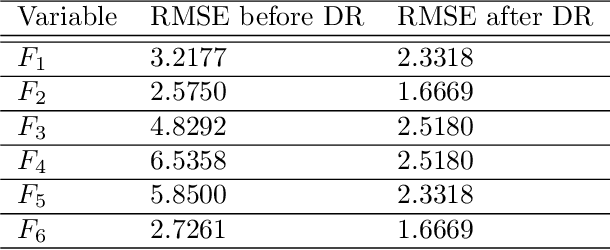
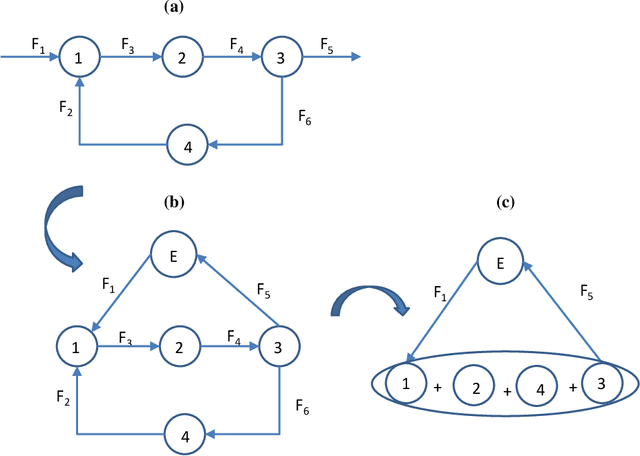
Data reconciliation (DR) and Principal Component Analysis (PCA) are two popular data analysis techniques in process industries. Data reconciliation is used to obtain accurate and consistent estimates of variables and parameters from erroneous measurements. PCA is primarily used as a method for reducing the dimensionality of high dimensional data and as a preprocessing technique for denoising measurements. These techniques have been developed and deployed independently of each other. The primary purpose of this article is to elucidate the close relationship between these two seemingly disparate techniques. This leads to a unified framework for applying PCA and DR. Further, we show how the two techniques can be deployed together in a collaborative and consistent manner to process data. The framework has been extended to deal with partially measured systems and to incorporate partial knowledge available about the process model.

Monotonous (Semi-)Nonnegative Matrix Factorization

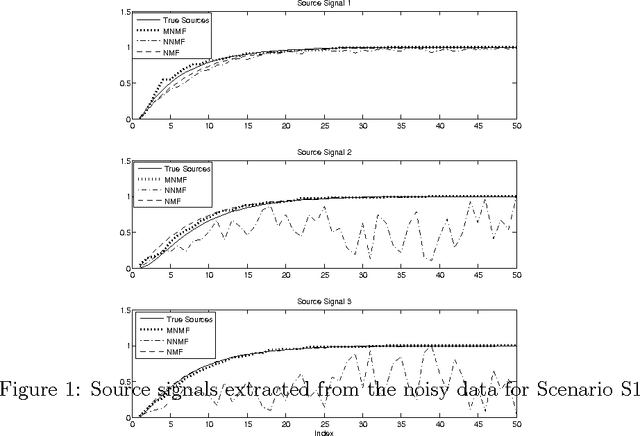
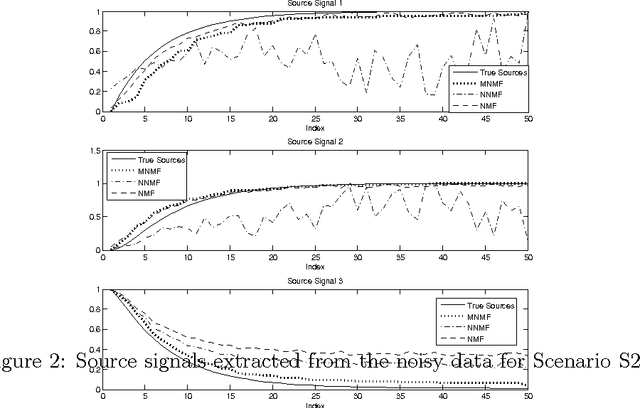
Nonnegative matrix factorization (NMF) factorizes a non-negative matrix into product of two non-negative matrices, namely a signal matrix and a mixing matrix. NMF suffers from the scale and ordering ambiguities. Often, the source signals can be monotonous in nature. For example, in source separation problem, the source signals can be monotonously increasing or decreasing while the mixing matrix can have nonnegative entries. NMF methods may not be effective for such cases as it suffers from the ordering ambiguity. This paper proposes an approach to incorporate notion of monotonicity in NMF, labeled as monotonous NMF. An algorithm based on alternating least-squares is proposed for recovering monotonous signals from a data matrix. Further, the assumption on mixing matrix is relaxed to extend monotonous NMF for data matrix with real numbers as entries. The approach is illustrated using synthetic noisy data. The results obtained by monotonous NMF are compared with standard NMF algorithms in the literature, and it is shown that monotonous NMF estimates source signals well in comparison to standard NMF algorithms when the underlying sources signals are monotonous.