Monotonous (Semi-)Nonnegative Matrix Factorization
Paper and Code
May 01, 2015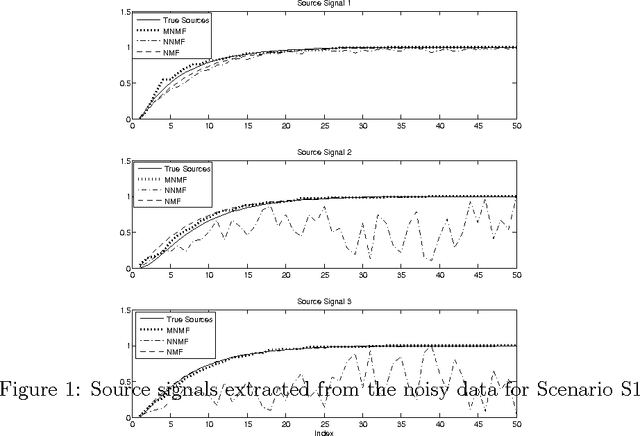
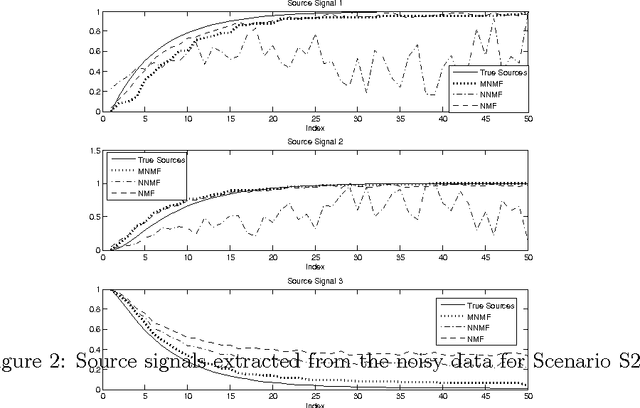
Nonnegative matrix factorization (NMF) factorizes a non-negative matrix into product of two non-negative matrices, namely a signal matrix and a mixing matrix. NMF suffers from the scale and ordering ambiguities. Often, the source signals can be monotonous in nature. For example, in source separation problem, the source signals can be monotonously increasing or decreasing while the mixing matrix can have nonnegative entries. NMF methods may not be effective for such cases as it suffers from the ordering ambiguity. This paper proposes an approach to incorporate notion of monotonicity in NMF, labeled as monotonous NMF. An algorithm based on alternating least-squares is proposed for recovering monotonous signals from a data matrix. Further, the assumption on mixing matrix is relaxed to extend monotonous NMF for data matrix with real numbers as entries. The approach is illustrated using synthetic noisy data. The results obtained by monotonous NMF are compared with standard NMF algorithms in the literature, and it is shown that monotonous NMF estimates source signals well in comparison to standard NMF algorithms when the underlying sources signals are monotonous.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge