Partial Inference in Structured Prediction

In this paper, we examine the problem of partial inference in the context of structured prediction. Using a generative model approach, we consider the task of maximizing a score function with unary and pairwise potentials in the space of labels on graphs. Employing a two-stage convex optimization algorithm for label recovery, we analyze the conditions under which a majority of the labels can be recovered. We introduce a novel perspective on the Karush-Kuhn-Tucker (KKT) conditions and primal and dual construction, and provide statistical and topological requirements for partial recovery with provable guarantees.

Exact Inference in High-order Structured Prediction

In this paper, we study the problem of inference in high-order structured prediction tasks. In the context of Markov random fields, the goal of a high-order inference task is to maximize a score function on the space of labels, and the score function can be decomposed into sum of unary and high-order potentials. We apply a generative model approach to study the problem of high-order inference, and provide a two-stage convex optimization algorithm for exact label recovery. We also provide a new class of hypergraph structural properties related to hyperedge expansion that drives the success in general high-order inference problems. Finally, we connect the performance of our algorithm and the hyperedge expansion property using a novel hypergraph Cheeger-type inequality.

Provable Guarantees for Sparsity Recovery with Deterministic Missing Data Patterns

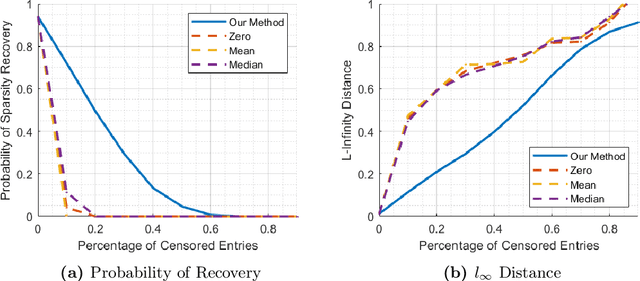
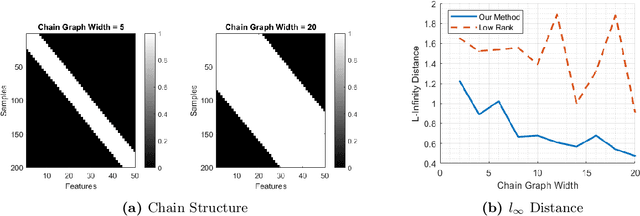
We study the problem of consistently recovering the sparsity pattern of a regression parameter vector from correlated observations governed by deterministic missing data patterns using Lasso. We consider the case in which the observed dataset is censored by a deterministic, non-uniform filter. Recovering the sparsity pattern in datasets with deterministic missing structure can be arguably more challenging than recovering in a uniformly-at-random scenario. In this paper, we propose an efficient algorithm for missing value imputation by utilizing the topological property of the censorship filter. We then provide novel theoretical results for exact recovery of the sparsity pattern using the proposed imputation strategy. Our analysis shows that, under certain statistical and topological conditions, the hidden sparsity pattern can be recovered consistently with high probability in polynomial time and logarithmic sample complexity.

Dual Convexified Convolutional Neural Networks

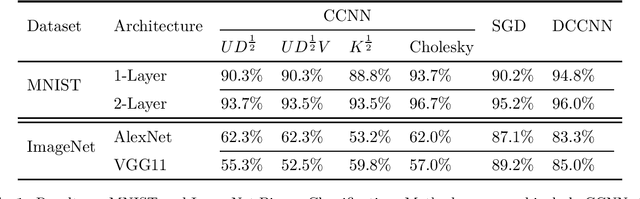
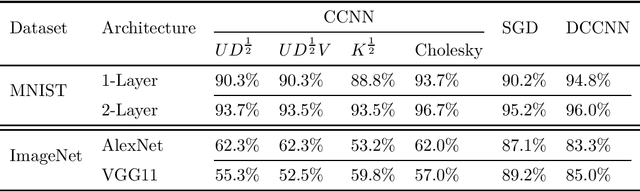
We propose the framework of dual convexified convolutional neural networks (DCCNNs). In this framework, we first introduce a primal learning problem motivated from convexified convolutional neural networks (CCNNs), and then construct the dual convex training program through careful analysis of the Karush-Kuhn-Tucker (KKT) conditions and Fenchel conjugates. Our approach reduces the memory overhead of constructing a large kernel matrix and eliminates the ambiguity of factorizing the matrix. Due to the low-rank structure in CCNNs and the related subdifferential of nuclear norms, there is no closed-form expression to recover the primal solution from the dual solution. To overcome this, we propose a highly novel weight recovery algorithm, which takes the dual solution and the kernel information as the input, and recovers the linear and convolutional weights of a CCNN. Furthermore, our recovery algorithm exploits the low-rank structure and imposes a small number of filters indirectly, which reduces the parameter size. As a result, DCCNNs inherit all the statistical benefits of CCNNs, while enjoying a more formal and efficient workflow.

Federated Myopic Community Detection with One-shot Communication

In this paper, we study the problem of recovering the community structure of a network under federated myopic learning. Under this paradigm, we have several clients, each of them having a myopic view, i.e., observing a small subgraph of the network. Each client sends a censored evidence graph to a central server. We provide an efficient algorithm, which computes a consensus signed weighted graph from clients evidence, and recovers the underlying network structure in the central server. We analyze the topological structure conditions of the network, as well as the signal and noise levels of the clients that allow for recovery of the network structure. Our analysis shows that exact recovery is possible and can be achieved in polynomial time. We also provide information-theoretic limits for the central server to recover the network structure from any single client evidence. Finally, as a byproduct of our analysis, we provide a novel Cheeger-type inequality for general signed weighted graphs.

A Thorough View of Exact Inference in Graphs from the Degree-4 Sum-of-Squares Hierarchy

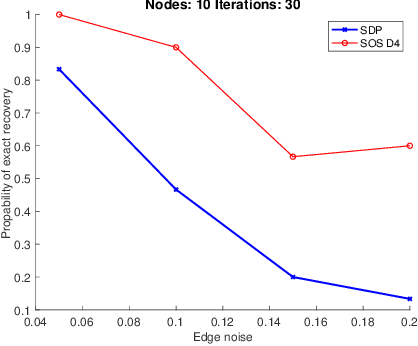
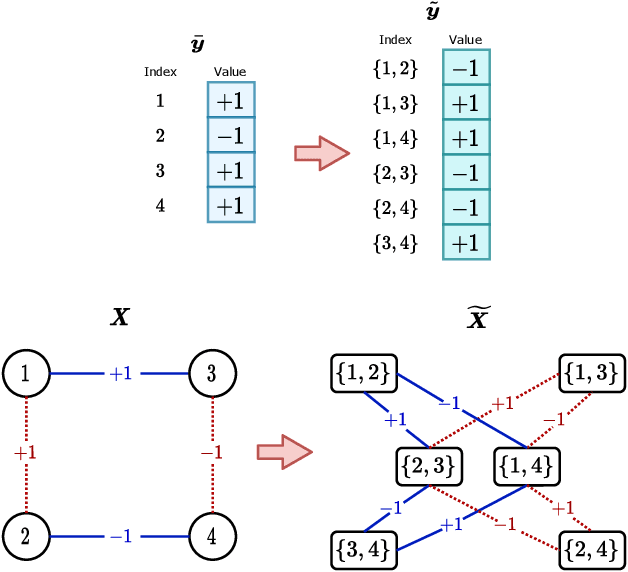
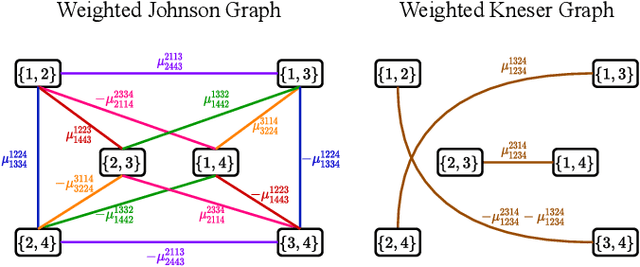
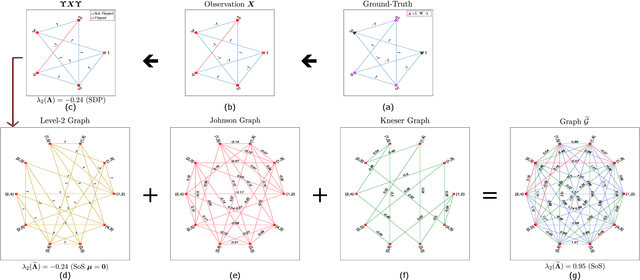
Performing inference in graphs is a common task within several machine learning problems, e.g., image segmentation, community detection, among others. For a given undirected connected graph, we tackle the statistical problem of exactly recovering an unknown ground-truth binary labeling of the nodes from a single corrupted observation of each edge. Such problem can be formulated as a quadratic combinatorial optimization problem over the boolean hypercube, where it has been shown before that one can (with high probability and in polynomial time) exactly recover the ground-truth labeling of graphs that have an isoperimetric number that grows with respect to the number of nodes (e.g., complete graphs, regular expanders). In this work, we apply a powerful hierarchy of relaxations, known as the sum-of-squares (SoS) hierarchy, to the combinatorial problem. Motivated by empirical evidence on the improvement in exact recoverability, we center our attention on the degree-4 SoS relaxation and set out to understand the origin of such improvement from a graph theoretical perspective. We show that the solution of the dual of the relaxed problem is related to finding edge weights of the Johnson and Kneser graphs, where the weights fulfill the SoS constraints and intuitively allow the input graph to increase its algebraic connectivity. Finally, as byproduct of our analysis, we derive a novel Cheeger-type lower bound for the algebraic connectivity of graphs with signed edge weights.

Information Theoretic Limits of Exact Recovery in Sub-hypergraph Models for Community Detection

In this paper, we study the information theoretic bounds for exact recovery in sub-hypergraph models for community detection. We define a general model called the $m-$uniform sub-hypergraph stochastic block model ($m-$ShSBM). Under the $m-$ShSBM, we use Fano's inequality to identify the region of model parameters where any algorithm fails to exactly recover the planted communities with a large probability. We also identify the region where a Maximum Likelihood Estimation (MLE) algorithm succeeds to exactly recover the communities with high probability. Our bounds are tight and pertain to the community detection problems in various models such as the planted hypergraph stochastic block model, the planted densest sub-hypergraph model, and the planted multipartite hypergraph model.

Exact Partitioning of High-order Planted Models with a Tensor Nuclear Norm Constraint

We study the problem of efficient exact partitioning of the hypergraphs generated by high-order planted models. A high-order planted model assumes some underlying cluster structures, and simulates high-order interactions by placing hyperedges among nodes. Example models include the disjoint hypercliques, the densest subhypergraphs, and the hypergraph stochastic block models. We show that exact partitioning of high-order planted models (a NP-hard problem in general) is achievable through solving a computationally efficient convex optimization problem with a tensor nuclear norm constraint. Our analysis provides the conditions for our approach to succeed on recovering the true underlying cluster structures, with high probability.

Exact Partitioning of High-order Models with a Novel Convex Tensor Cone Relaxation

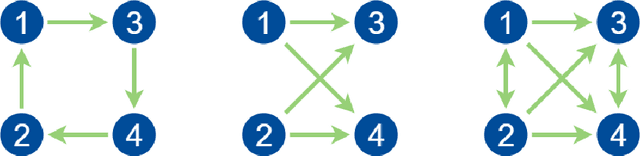
In this paper we propose the first correct poly-time algorithm for exact partitioning of high-order models (a worst case NP-hard problem). We define a general class of $m$-degree Homogeneous Polynomial Models, which subsumes several examples motivated from prior literature. Exact partitioning can be formulated as a tensor optimization problem. We relax this NP-hard problem to a convex conic form problem (poly-time solvable by interior point methods). To this end, we carefully define the positive semidefinite tensor cone, and show its convexity, and the convexity of its dual cone. This allows us to construct a primal-dual certificate to show that the solution of the convex relaxation is correct (equal to the unobserved true group assignment) under some sample complexity conditions.

Exact Recovery in the Latent Space Model

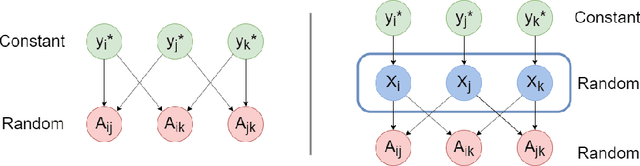
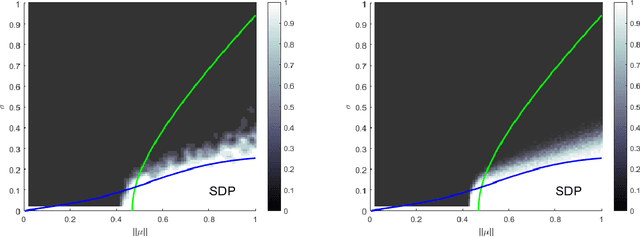
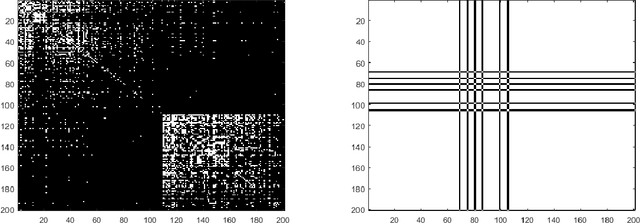
We analyze the necessary and sufficient conditions for exact recovery of the symmetric Latent Space Model (LSM) with two communities. In a LSM, each node is associated with a latent vector following some probability distribution. We show that exact recovery can be achieved using a semidefinite programming approach.