Dual Convexified Convolutional Neural Networks
Paper and Code
May 27, 2022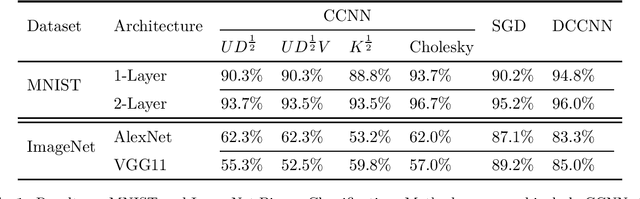
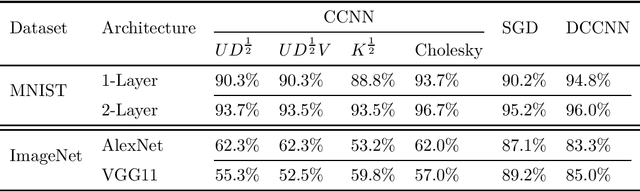
We propose the framework of dual convexified convolutional neural networks (DCCNNs). In this framework, we first introduce a primal learning problem motivated from convexified convolutional neural networks (CCNNs), and then construct the dual convex training program through careful analysis of the Karush-Kuhn-Tucker (KKT) conditions and Fenchel conjugates. Our approach reduces the memory overhead of constructing a large kernel matrix and eliminates the ambiguity of factorizing the matrix. Due to the low-rank structure in CCNNs and the related subdifferential of nuclear norms, there is no closed-form expression to recover the primal solution from the dual solution. To overcome this, we propose a highly novel weight recovery algorithm, which takes the dual solution and the kernel information as the input, and recovers the linear and convolutional weights of a CCNN. Furthermore, our recovery algorithm exploits the low-rank structure and imposes a small number of filters indirectly, which reduces the parameter size. As a result, DCCNNs inherit all the statistical benefits of CCNNs, while enjoying a more formal and efficient workflow.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge