Faster Acceleration for Steepest Descent

We propose a new accelerated first-order method for convex optimization under non-Euclidean smoothness assumptions. In contrast to standard acceleration techniques, our approach uses primal-dual iterate sequences taken with respect to differing norms, which are then coupled using an implicitly determined interpolation parameter. For $\ell_p$ norm smooth problems in $d$ dimensions, our method provides an iteration complexity improvement of up to $O(d^{1-\frac{2}{p}})$ in terms of calls to a first-order oracle, thereby allowing us to circumvent long-standing barriers in accelerated non-Euclidean steepest descent.

Tight Lower Bounds under Asymmetric High-Order Hölder Smoothness and Uniform Convexity

In this paper, we provide tight lower bounds for the oracle complexity of minimizing high-order H\"older smooth and uniformly convex functions. Specifically, for a function whose $p^{th}$-order derivatives are H\"older continuous with degree $\nu$ and parameter $H$, and that is uniformly convex with degree $q$ and parameter $\sigma$, we focus on two asymmetric cases: (1) $q > p + \nu$, and (2) $q < p+\nu$. Given up to $p^{th}$-order oracle access, we establish worst-case oracle complexities of $\Omega\left( \left( \frac{H}{\sigma}\right)^\frac{2}{3(p+\nu)-2}\left( \frac{\sigma}{\epsilon}\right)^\frac{2(q-p-\nu)}{q(3(p+\nu)-2)}\right)$ with a truncated-Gaussian smoothed hard function in the first case and $\Omega\left(\left(\frac{H}{\sigma}\right)^\frac{2}{3(p+\nu)-2}+ \log^2\left(\frac{\sigma^{p+\nu}}{H^q}\right)^\frac{1}{p+\nu-q}\right)$ in the second case, for reaching an $\epsilon$-approximate solution in terms of the optimality gap. Our analysis generalizes previous lower bounds for functions under first- and second-order smoothness as well as those for uniformly convex functions, and furthermore our results match the corresponding upper bounds in the general setting.

Federated Composite Saddle Point Optimization

Federated learning (FL) approaches for saddle point problems (SPP) have recently gained in popularity due to the critical role they play in machine learning (ML). Existing works mostly target smooth unconstrained objectives in Euclidean space, whereas ML problems often involve constraints or non-smooth regularization, which results in a need for composite optimization. Addressing these issues, we propose Federated Dual Extrapolation (FeDualEx), an extra-step primal-dual algorithm, which is the first of its kind that encompasses both saddle point optimization and composite objectives under the FL paradigm. Both the convergence analysis and the empirical evaluation demonstrate the effectiveness of FeDualEx in these challenging settings. In addition, even for the sequential version of FeDualEx, we provide rates for the stochastic composite saddle point setting which, to our knowledge, are not found in prior literature.

Dual Convexified Convolutional Neural Networks

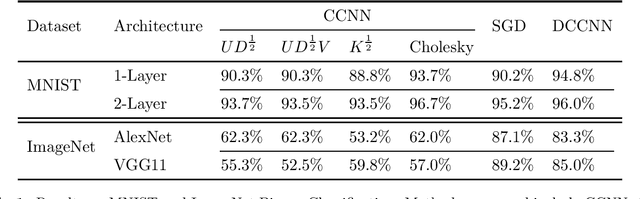
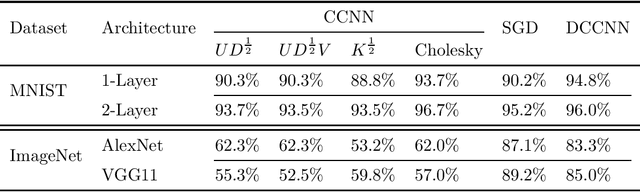
We propose the framework of dual convexified convolutional neural networks (DCCNNs). In this framework, we first introduce a primal learning problem motivated from convexified convolutional neural networks (CCNNs), and then construct the dual convex training program through careful analysis of the Karush-Kuhn-Tucker (KKT) conditions and Fenchel conjugates. Our approach reduces the memory overhead of constructing a large kernel matrix and eliminates the ambiguity of factorizing the matrix. Due to the low-rank structure in CCNNs and the related subdifferential of nuclear norms, there is no closed-form expression to recover the primal solution from the dual solution. To overcome this, we propose a highly novel weight recovery algorithm, which takes the dual solution and the kernel information as the input, and recovers the linear and convolutional weights of a CCNN. Furthermore, our recovery algorithm exploits the low-rank structure and imposes a small number of filters indirectly, which reduces the parameter size. As a result, DCCNNs inherit all the statistical benefits of CCNNs, while enjoying a more formal and efficient workflow.

Hindsight Trust Region Policy Optimization

As reinforcement learning continues to drive machine intelligence beyond its conventional boundary, unsubstantial practices in sparse reward environment severely limit further applications in a broader range of advanced fields. Motivated by the demand for an effective deep reinforcement learning algorithm that accommodates sparse reward environment, this paper presents Hindsight Trust Region Policy Optimization (Hindsight TRPO), a method that efficiently utilizes interactions in sparse reward conditions and maintains learning stability by restricting variance during the policy update process. Firstly, the hindsight methodology is expanded to TRPO, an advanced and efficient on-policy policy gradient method. Then, under the condition that the distributions are close, the KL-divergence is appropriately approximated by another $f$-divergence. Such approximation results in the decrease of variance during KL-divergence estimation and alleviates the instability during policy update. Experimental results on both discrete and continuous benchmark tasks demonstrate that Hindsight TRPO converges steadily and significantly faster than previous policy gradient methods. It achieves effective performances and high data-efficiency for training policies in sparse reward environments.

ROI-based Robotic Grasp Detection for Object Overlapping Scenes

Grasp detection with consideration of the affiliations between grasps and their owner in object overlapping scenes is a necessary and challenging task for the practical use of the robotic grasping approach. In this paper, a robotic grasp detection algorithm named ROI-GD is proposed to provide a feasible solution to this problem based on Region of Interest (ROI), which is the region proposal for objects. ROI-GD uses features from ROIs to detect grasps instead of the whole scene. It has two stages: the first stage is to provide ROIs in the input image and the second-stage is the grasp detector based on ROI features. We also contribute a multi-object grasp dataset, which is much larger than Cornell Grasp Dataset, by labeling Visual Manipulation Relationship Dataset. Experimental results demonstrate that ROI-GD performs much better in object overlapping scenes and at the meantime, remains comparable with state-of-the-art grasp detection algorithms on Cornell Grasp Dataset and Jacquard Dataset. Robotic experiments demonstrate that ROI-GD can help robots grasp the target in single-object and multi-object scenes with the overall success rates of 92.5% and 83.8% respectively.

A Multi-task Convolutional Neural Network for Autonomous Robotic Grasping in Object Stacking Scenes

Autonomous robotic grasping plays an important role in intelligent robotics. However, how to help the robot grasp specific objects in object stacking scenes is still an open problem, because there are two main challenges for autonomous robots: (1)it is a comprehensive task to know what and how to grasp; (2)it is hard to deal with the situations in which the target is hidden or covered by other objects. In this paper, we propose a multi-task convolutional neural network for autonomous robotic grasping, which can help the robot find the target, make the plan for grasping and finally grasp the target step by step in object stacking scenes. We integrate vision-based robotic grasping detection and visual manipulation relationship reasoning in one single deep network and build the autonomous robotic grasping system. Experimental results demonstrate that with our model, Baxter robot can autonomously grasp the target with a success rate of 90.6%, 71.9% and 59.4% in object cluttered scenes, familiar stacking scenes and complex stacking scenes respectively.