Identifying General Mechanism Shifts in Linear Causal Representations

We consider the linear causal representation learning setting where we observe a linear mixing of $d$ unknown latent factors, which follow a linear structural causal model. Recent work has shown that it is possible to recover the latent factors as well as the underlying structural causal model over them, up to permutation and scaling, provided that we have at least $d$ environments, each of which corresponds to perfect interventions on a single latent node (factor). After this powerful result, a key open problem faced by the community has been to relax these conditions: allow for coarser than perfect single-node interventions, and allow for fewer than $d$ of them, since the number of latent factors $d$ could be very large. In this work, we consider precisely such a setting, where we allow a smaller than $d$ number of environments, and also allow for very coarse interventions that can very coarsely \textit{change the entire causal graph over the latent factors}. On the flip side, we relax what we wish to extract to simply the \textit{list of nodes that have shifted between one or more environments}. We provide a surprising identifiability result that it is indeed possible, under some very mild standard assumptions, to identify the set of shifted nodes. Our identifiability proof moreover is a constructive one: we explicitly provide necessary and sufficient conditions for a node to be a shifted node, and show that we can check these conditions given observed data. Our algorithm lends itself very naturally to the sample setting where instead of just interventional distributions, we are provided datasets of samples from each of these distributions. We corroborate our results on both synthetic experiments as well as an interesting psychometric dataset. The code can be found at https://github.com/TianyuCodings/iLCS.

Likelihood-based Differentiable Structure Learning

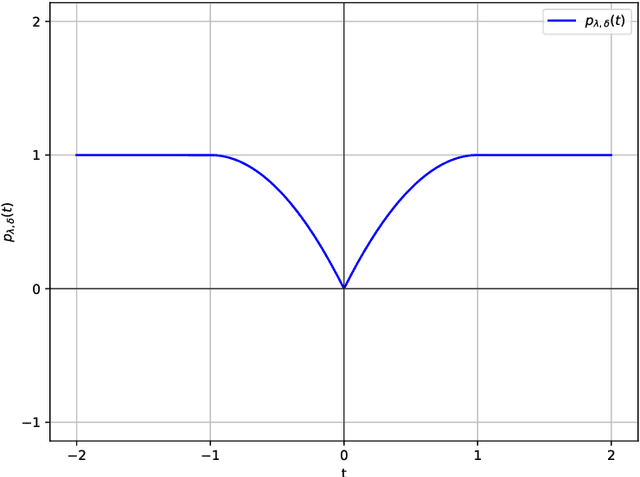
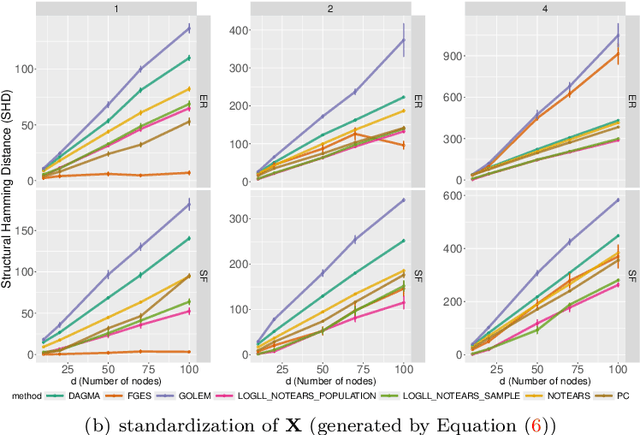
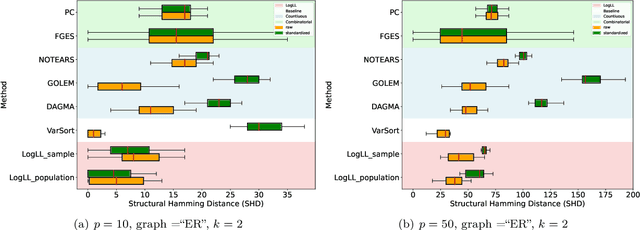
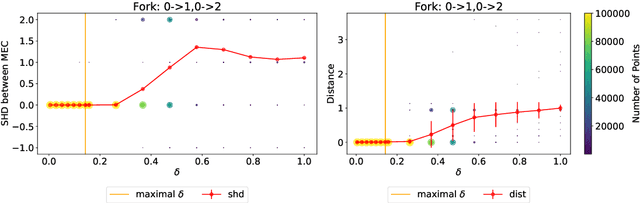
Existing approaches to differentiable structure learning of directed acyclic graphs (DAGs) rely on strong identifiability assumptions in order to guarantee that global minimizers of the acyclicity-constrained optimization problem identifies the true DAG. Moreover, it has been observed empirically that the optimizer may exploit undesirable artifacts in the loss function. We explain and remedy these issues by studying the behavior of differentiable acyclicity-constrained programs under general likelihoods with multiple global minimizers. By carefully regularizing the likelihood, it is possible to identify the sparsest model in the Markov equivalence class, even in the absence of an identifiable parametrization. We first study the Gaussian case in detail, showing how proper regularization of the likelihood defines a score that identifies the sparsest model. Assuming faithfulness, it also recovers the Markov equivalence class. These results are then generalized to general models and likelihoods, where the same claims hold. These theoretical results are validated empirically, showing how this can be done using standard gradient-based optimizers, thus paving the way for differentiable structure learning under general models and losses.

Bayesian Dynamic DAG Learning: Application in Discovering Dynamic Effective Connectome of Brain

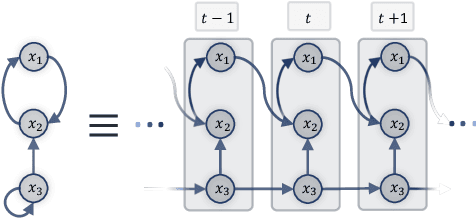
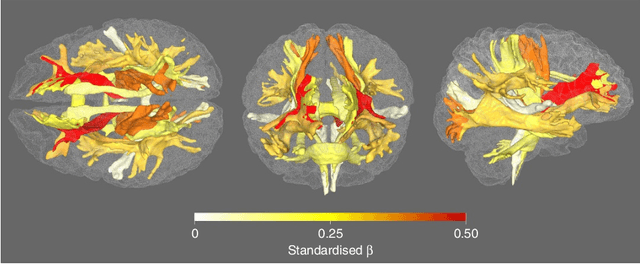
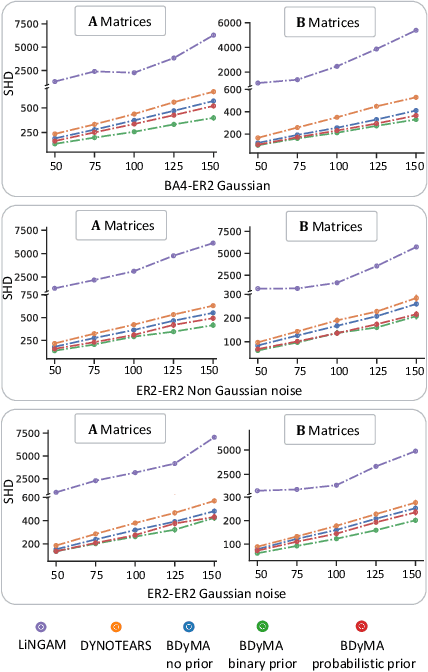
Understanding the complex mechanisms of the brain can be unraveled by extracting the Dynamic Effective Connectome (DEC). Recently, score-based Directed Acyclic Graph (DAG) discovery methods have shown significant improvements in extracting the causal structure and inferring effective connectivity. However, learning DEC through these methods still faces two main challenges: one with the fundamental impotence of high-dimensional dynamic DAG discovery methods and the other with the low quality of fMRI data. In this paper, we introduce Bayesian Dynamic DAG learning with M-matrices Acyclicity characterization \textbf{(BDyMA)} method to address the challenges in discovering DEC. The presented dynamic causal model enables us to discover bidirected edges as well. Leveraging an unconstrained framework in the BDyMA method leads to more accurate results in detecting high-dimensional networks, achieving sparser outcomes, making it particularly suitable for extracting DEC. Additionally, the score function of the BDyMA method allows the incorporation of prior knowledge into the process of dynamic causal discovery which further enhances the accuracy of results. Comprehensive simulations on synthetic data and experiments on Human Connectome Project (HCP) data demonstrate that our method can handle both of the two main challenges, yielding more accurate and reliable DEC compared to state-of-the-art and baseline methods. Additionally, we investigate the trustworthiness of DTI data as prior knowledge for DEC discovery and show the improvements in DEC discovery when the DTI data is incorporated into the process.

Global Optimality in Bivariate Gradient-based DAG Learning

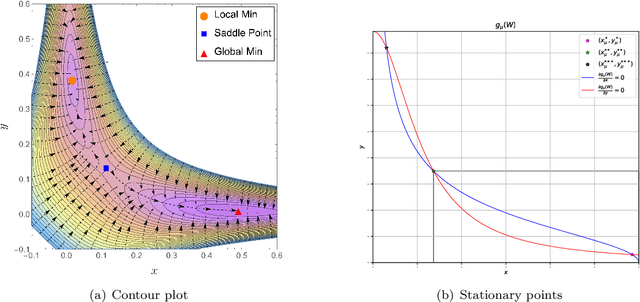
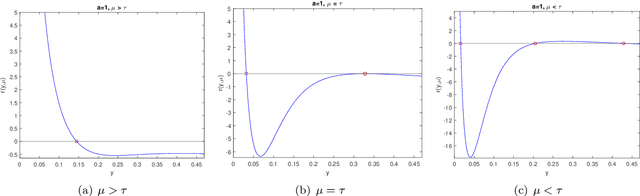
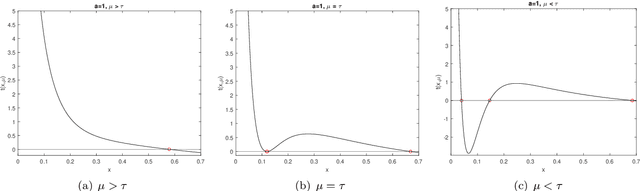
Recently, a new class of non-convex optimization problems motivated by the statistical problem of learning an acyclic directed graphical model from data has attracted significant interest. While existing work uses standard first-order optimization schemes to solve this problem, proving the global optimality of such approaches has proven elusive. The difficulty lies in the fact that unlike other non-convex problems in the literature, this problem is not "benign", and possesses multiple spurious solutions that standard approaches can easily get trapped in. In this paper, we prove that a simple path-following optimization scheme globally converges to the global minimum of the population loss in the bivariate setting.

iSCAN: Identifying Causal Mechanism Shifts among Nonlinear Additive Noise Models

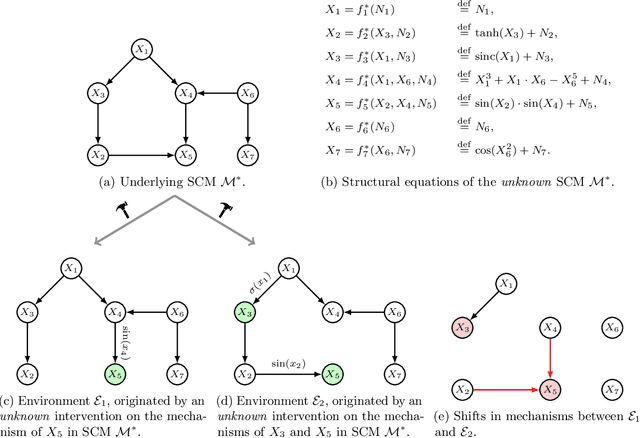
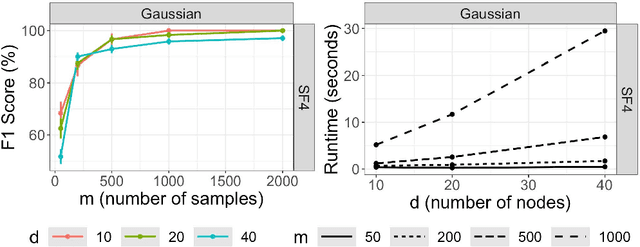
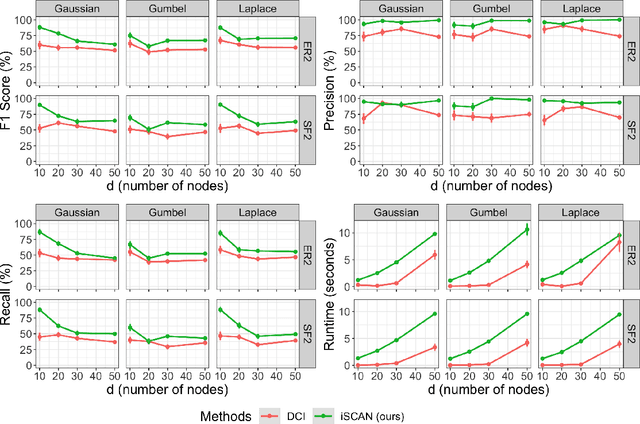
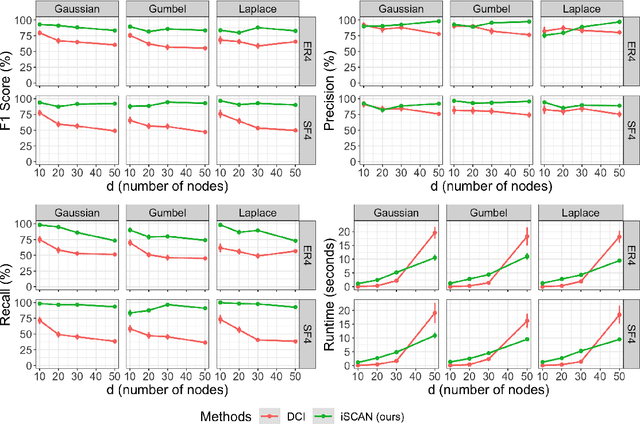
Structural causal models (SCMs) are widely used in various disciplines to represent causal relationships among variables in complex systems. Unfortunately, the true underlying directed acyclic graph (DAG) structure is often unknown, and determining it from observational or interventional data remains a challenging task. However, in many situations, the end goal is to identify changes (shifts) in causal mechanisms between related SCMs rather than recovering the entire underlying DAG structure. Examples include analyzing gene regulatory network structure changes between healthy and cancerous individuals or understanding variations in biological pathways under different cellular contexts. This paper focuses on identifying $\textit{functional}$ mechanism shifts in two or more related SCMs over the same set of variables -- $\textit{without estimating the entire DAG structure of each SCM}$. Prior work under this setting assumed linear models with Gaussian noises; instead, in this work we assume that each SCM belongs to the more general class of nonlinear additive noise models (ANMs). A key contribution of this work is to show that the Jacobian of the score function for the $\textit{mixture distribution}$ allows for identification of shifts in general non-parametric functional mechanisms. Once the shifted variables are identified, we leverage recent work to estimate the structural differences, if any, for the shifted variables. Experiments on synthetic and real-world data are provided to showcase the applicability of this approach.

Optimizing NOTEARS Objectives via Topological Swaps

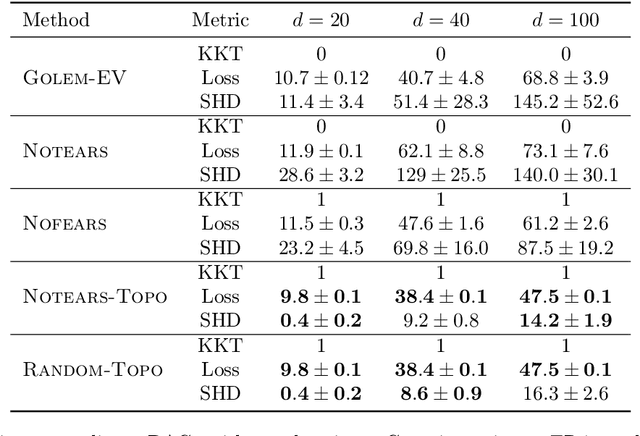
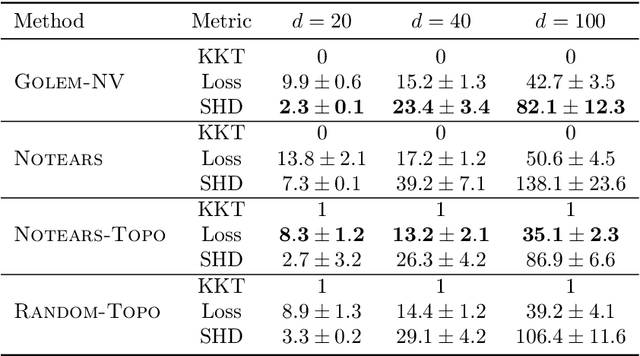
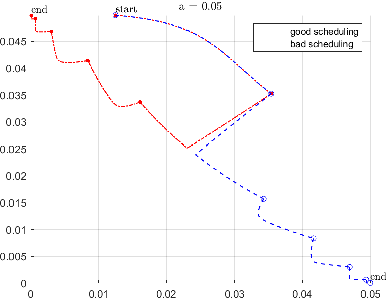
Recently, an intriguing class of non-convex optimization problems has emerged in the context of learning directed acyclic graphs (DAGs). These problems involve minimizing a given loss or score function, subject to a non-convex continuous constraint that penalizes the presence of cycles in a graph. In this work, we delve into the optimization challenges associated with this class of non-convex programs. To address these challenges, we propose a bi-level algorithm that leverages the non-convex constraint in a novel way. The outer level of the algorithm optimizes over topological orders by iteratively swapping pairs of nodes within the topological order of a DAG. A key innovation of our approach is the development of an effective method for generating a set of candidate swapping pairs for each iteration. At the inner level, given a topological order, we utilize off-the-shelf solvers that can handle linear constraints. The key advantage of our proposed algorithm is that it is guaranteed to find a local minimum or a KKT point under weaker conditions compared to previous work and finds solutions with lower scores. Extensive experiments demonstrate that our method outperforms state-of-the-art approaches in terms of achieving a better score. Additionally, our method can also be used as a post-processing algorithm to significantly improve the score of other algorithms. Code implementing the proposed method is available at https://github.com/duntrain/topo.

DAGMA: Learning DAGs via M-matrices and a Log-Determinant Acyclicity Characterization

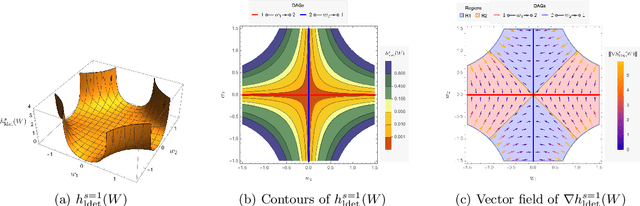
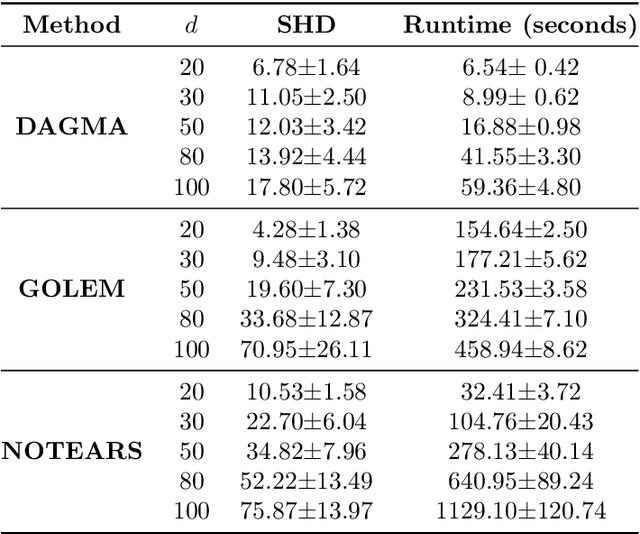
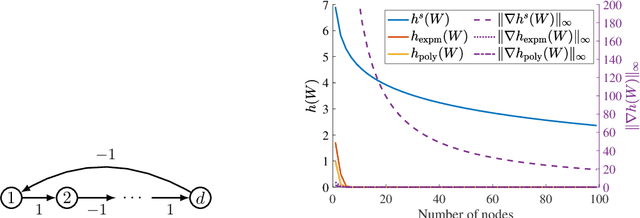
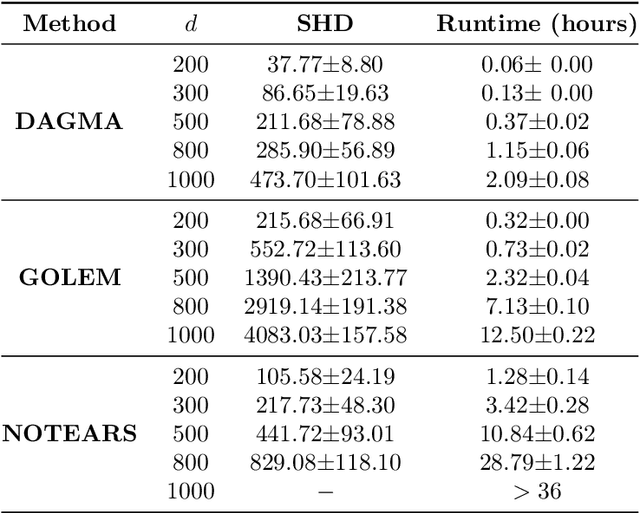
The combinatorial problem of learning directed acyclic graphs (DAGs) from data was recently framed as a purely continuous optimization problem by leveraging a differentiable acyclicity characterization of DAGs based on the trace of a matrix exponential function. Existing acyclicity characterizations are based on the idea that powers of an adjacency matrix contain information about walks and cycles. In this work, we propose a $\textit{fundamentally different}$ acyclicity characterization based on the log-determinant (log-det) function, which leverages the nilpotency property of DAGs. To deal with the inherent asymmetries of a DAG, we relate the domain of our log-det characterization to the set of $\textit{M-matrices}$, which is a key difference to the classical log-det function defined over the cone of positive definite matrices. Similar to acyclicity functions previously proposed, our characterization is also exact and differentiable. However, when compared to existing characterizations, our log-det function: (1) Is better at detecting large cycles; (2) Has better-behaved gradients; and (3) Its runtime is in practice about an order of magnitude faster. From the optimization side, we drop the typically used augmented Lagrangian scheme, and propose DAGMA ($\textit{Directed Acyclic Graphs via M-matrices for Acyclicity}$), a method that resembles the central path for barrier methods. Each point in the central path of DAGMA is a solution to an unconstrained problem regularized by our log-det function, then we show that at the limit of the central path the solution is guaranteed to be a DAG. Finally, we provide extensive experiments for $\textit{linear}$ and $\textit{nonlinear}$ SEMs, and show that our approach can reach large speed-ups and smaller structural Hamming distances against state-of-the-art methods.

On the Fundamental Limits of Exact Inference in Structured Prediction

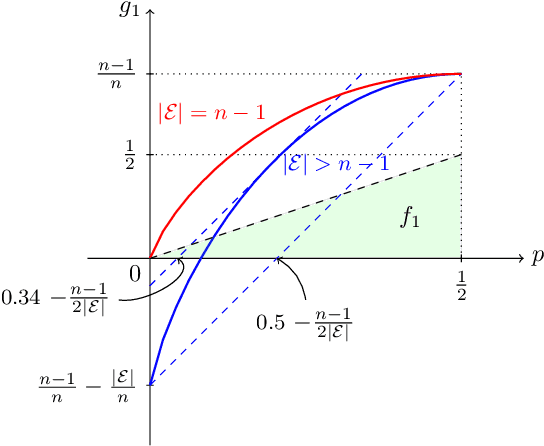
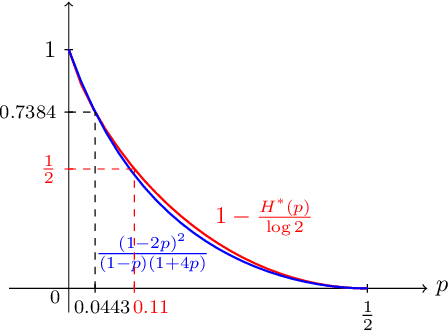
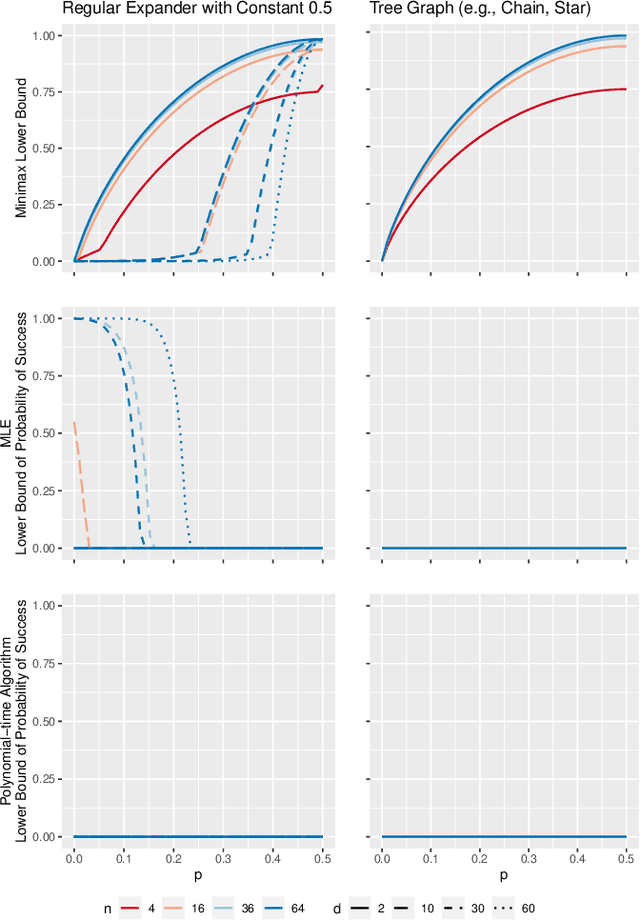
Inference is a main task in structured prediction and it is naturally modeled with a graph. In the context of Markov random fields, noisy observations corresponding to nodes and edges are usually involved, and the goal of exact inference is to recover the unknown true label for each node precisely. The focus of this paper is on the fundamental limits of exact recovery irrespective of computational efficiency, assuming the generative process proposed by Globerson et al. (2015). We derive the necessary condition for any algorithm and the sufficient condition for maximum likelihood estimation to achieve exact recovery with high probability, and reveal that the sufficient and necessary conditions are tight up to a logarithmic factor for a wide range of graphs. Finally, we show that there exists a gap between the fundamental limits and the performance of the computationally tractable method of Bello and Honorio (2019), which implies the need for further development of algorithms for exact inference.

A Thorough View of Exact Inference in Graphs from the Degree-4 Sum-of-Squares Hierarchy

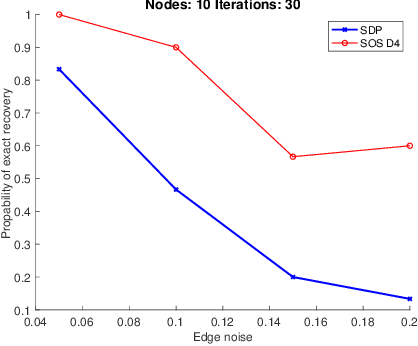
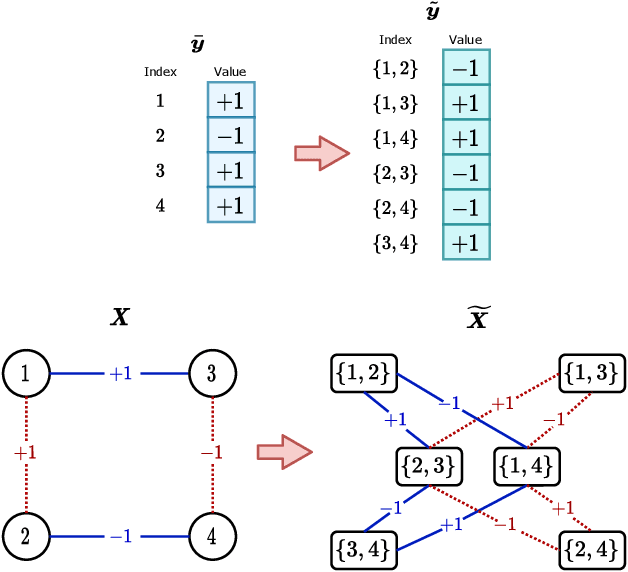
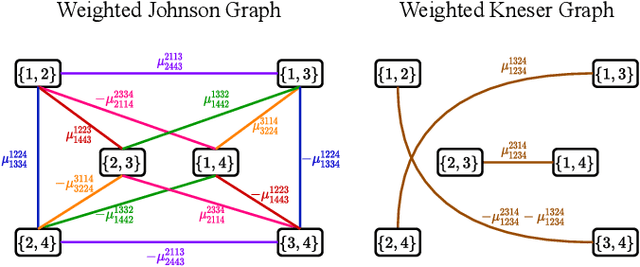
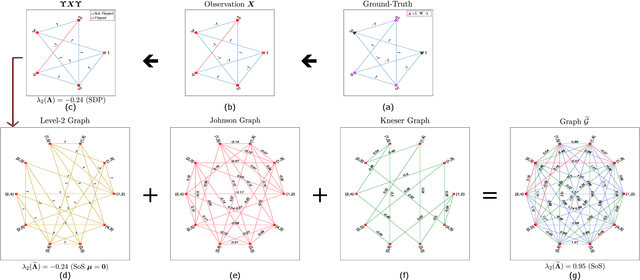
Performing inference in graphs is a common task within several machine learning problems, e.g., image segmentation, community detection, among others. For a given undirected connected graph, we tackle the statistical problem of exactly recovering an unknown ground-truth binary labeling of the nodes from a single corrupted observation of each edge. Such problem can be formulated as a quadratic combinatorial optimization problem over the boolean hypercube, where it has been shown before that one can (with high probability and in polynomial time) exactly recover the ground-truth labeling of graphs that have an isoperimetric number that grows with respect to the number of nodes (e.g., complete graphs, regular expanders). In this work, we apply a powerful hierarchy of relaxations, known as the sum-of-squares (SoS) hierarchy, to the combinatorial problem. Motivated by empirical evidence on the improvement in exact recoverability, we center our attention on the degree-4 SoS relaxation and set out to understand the origin of such improvement from a graph theoretical perspective. We show that the solution of the dual of the relaxed problem is related to finding edge weights of the Johnson and Kneser graphs, where the weights fulfill the SoS constraints and intuitively allow the input graph to increase its algebraic connectivity. Finally, as byproduct of our analysis, we derive a novel Cheeger-type lower bound for the algebraic connectivity of graphs with signed edge weights.

Inverse Reinforcement Learning in the Continuous Setting with Formal Guarantees

Inverse Reinforcement Learning (IRL) is the problem of finding a reward function which describes observed/known expert behavior. IRL is useful for automated control in situations where the reward function is difficult to specify manually, which impedes reinforcement learning. We provide a new IRL algorithm for the continuous state space setting with unknown transition dynamics by modeling the system using a basis of orthonormal functions. We provide a proof of correctness and formal guarantees on the sample and time complexity of our algorithm.