On the Fundamental Limits of Exact Inference in Structured Prediction
Paper and Code
Feb 17, 2021
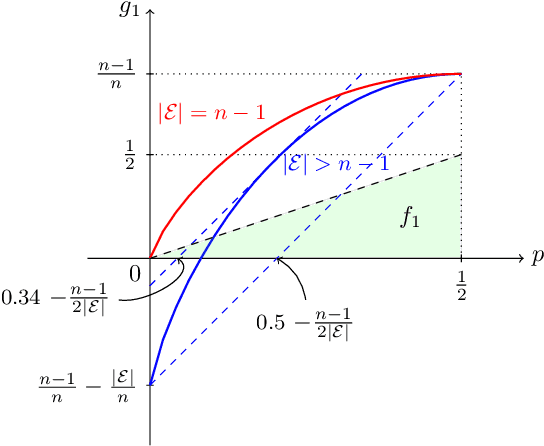
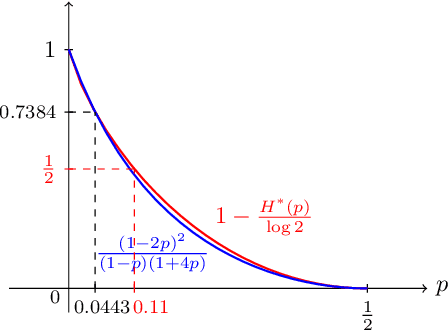
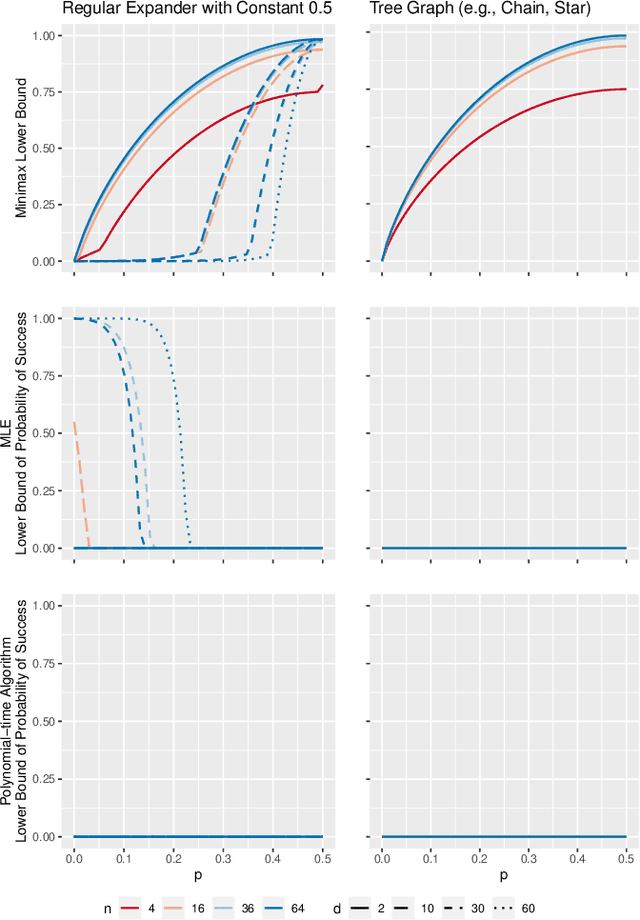
Inference is a main task in structured prediction and it is naturally modeled with a graph. In the context of Markov random fields, noisy observations corresponding to nodes and edges are usually involved, and the goal of exact inference is to recover the unknown true label for each node precisely. The focus of this paper is on the fundamental limits of exact recovery irrespective of computational efficiency, assuming the generative process proposed by Globerson et al. (2015). We derive the necessary condition for any algorithm and the sufficient condition for maximum likelihood estimation to achieve exact recovery with high probability, and reveal that the sufficient and necessary conditions are tight up to a logarithmic factor for a wide range of graphs. Finally, we show that there exists a gap between the fundamental limits and the performance of the computationally tractable method of Bello and Honorio (2019), which implies the need for further development of algorithms for exact inference.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge