Uncertainty Awareness in Wireless Communications, Sensing, and Learning

Wireless communications and sensing (WCS) establish the backbone of modern information exchange and environment perception. Typical applications range from mobile networks and the Internet of Things to radar and sensor grids. The incorporation of machine learning further expands WCS's boundaries, unlocking automated and high-quality data analytics, together with advisable and efficient decision-making. Despite transformative capabilities, wireless systems often face numerous uncertainties in design and operation, such as modeling errors due to incomplete physical knowledge, statistical errors arising from data scarcity, measurement errors caused by sensor imperfections, computational errors owing to resource limitation, and unpredictability of environmental evolution. Once ignored, these uncertainties can lead to severe outcomes, e.g., performance degradation, system untrustworthiness, inefficient resource utilization, and security vulnerabilities. As such, this article reviews mature and emerging architectural, computational, and operational countermeasures, encompassing uncertainty-aware designs of signals and systems (e.g., diversity, adaptivity, modularity), as well as uncertainty-aware modeling and computational frameworks (e.g., risk-informed optimization, robust signal processing, and trustworthy machine learning). Trade-offs to employ these methods, e.g., robustness vs optimality, are also highlighted.

Robust Beamforming with Application in High-Resolution Sensing

As a fundamental technique in array signal processing, beamforming plays a crucial role in amplifying signals of interest while mitigating interference and noise. When uncertainties exist in the signal model or the data size of snapshots is limited, the performance of beamformers significantly degrades. In this article, we comprehensively study the conceptual system, theoretical analysis, and algorithmic design for robust beamforming. Particularly, four technical approaches for robust beamforming are discussed, including locally robust beamforming, globally robust beamforming, regularized beamforming, and Bayesian-nonparametric beamforming. In addition, we investigate the equivalence among the methods and suggest a unified robust beamforming framework. As an application example, we show that the resolution of robust beamformers for direction-of-arrival (DoA) estimation can be greatly refined by incorporating the characteristics of subspace methods.

Machine Learning in Communications: A Road to Intelligent Transmission and Processing

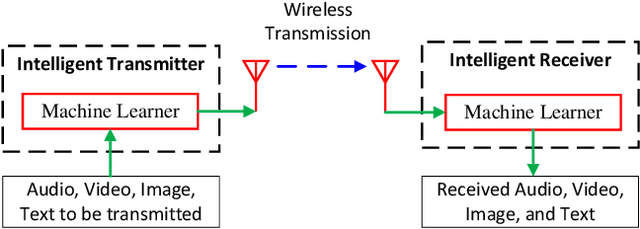
Prior to the era of artificial intelligence and big data, wireless communications primarily followed a conventional research route involving problem analysis, model building and calibration, algorithm design and tuning, and holistic and empirical verification. However, this methodology often encountered limitations when dealing with large-scale and complex problems and managing dynamic and massive data, resulting in inefficiencies and limited performance of traditional communication systems and methods. As such, wireless communications have embraced the revolutionary impact of artificial intelligence and machine learning, giving birth to more adaptive, efficient, and intelligent systems and algorithms. This technological shift opens a road to intelligent information transmission and processing. This overview article discusses the typical roles of machine learning in intelligent wireless communications, as well as its features, challenges, and practical considerations.

Distributionally Robust Beamforming and Estimation of Wireless Signals

This paper investigates signal estimation in wireless transmission from the perspective of statistical machine learning, where the transmitted signals may be from an integrated sensing and communication system; that is, 1) signals may be not only discrete constellation points but also arbitrary complex values; 2) signals may be spatially correlated. Particular attention is paid to handling various uncertainties such as the uncertainty of the transmitting signal covariance, the uncertainty of the channel matrix, the uncertainty of the channel noise covariance, the existence of channel impulse noises (i.e., outliers), and the limited sample size of pilots. To proceed, a distributionally robust machine learning framework that is insensitive to the above uncertainties is proposed for beamforming (at the receiver) and estimation of wireless signals, which reveals that channel estimation is not a necessary operation. For optimal linear estimation, the proposed framework includes several existing beamformers as special cases such as diagonal loading and eigenvalue thresholding. For optimal nonlinear estimation, estimators are limited in reproducing kernel Hilbert spaces and neural network function spaces, and corresponding uncertainty-aware solutions (e.g., kernelized diagonal loading) are derived. In addition, we prove that the ridge and kernel ridge regression methods in machine learning are distributionally robust against diagonal perturbation in feature covariance.

Uncertainty-Aware Bayes' Rule and Its Applications

Bayes' rule has enabled innumerable powerful algorithms of statistical signal processing and statistical machine learning. However, when there exist model misspecifications in prior distributions and/or data distributions, the direct application of Bayes' rule is questionable. Philosophically, the key is to balance the relative importance of prior and data distributions when calculating posterior distributions: if prior (resp. data) distributions are overly conservative, we should upweight the prior belief (resp. data evidence); if prior (resp. data) distributions are overly opportunistic, we should downweight the prior belief (resp. data evidence). This paper derives a generalized Bayes' rule, called uncertainty-aware Bayes' rule, to technically realize the above philosophy, i.e., to combat the model uncertainties in prior distributions and/or data distributions. Simulated and real-world experiments showcase the superiority of the presented uncertainty-aware Bayes' rule over the conventional Bayes' rule: In particular, the uncertainty-aware Kalman filter, the uncertainty-aware particle filter, and the uncertainty-aware interactive multiple model filter are suggested and validated.

Robust Waveform Design for Integrated Sensing and Communication

Integrated sensing and communication (ISAC), which enables hardware, resources (e.g., spectra), and waveforms sharing, is becoming a key feature in future-generation communication systems. This paper investigates robust waveform design for ISAC systems when the underlying true communication channels (e.g. time-selective ones) are not accurately known. With uncertainties in nominal communication channel models, the nominally-estimated communication performance may be not achievable in practice; i.e., the communication performance of ISAC systems cannot be guaranteed. Therefore, we formulate robust waveform design problems by studying the worst-case channels and prove that the robustly-estimated performance is guaranteed to be attainable in real-world operation. As a consequence, the reliability of ISAC systems in terms of communication performance is improved. The robust waveform design problems are shown to be non-convex, non-differentiable, and high-dimensional, which cannot be solved using existing optimization techniques. Therefore, we develop a computationally-efficient and globally-optimal algorithm to solve them. Simulation results show that the robustly-estimated communication performance can be ensured to be practically reachable while the nominally-estimated performance cannot, which validates the value of robust design.

Learning Against Distributional Uncertainty: On the Trade-off Between Robustness and Specificity

Trustworthy machine learning aims at combating distributional uncertainties in training data distributions compared to population distributions. Typical treatment frameworks include the Bayesian approach, (min-max) distributionally robust optimization (DRO), and regularization. However, two issues have to be raised: 1) All these methods are biased estimators of the true optimal cost; 2) the prior distribution in the Bayesian method, the radius of the distributional ball in the DRO method, and the regularizer in the regularization method are difficult to specify. This paper studies a new framework that unifies the three approaches and that addresses the two challenges mentioned above. The asymptotic properties (e.g., consistency and asymptotic normalities), non-asymptotic properties (e.g., unbiasedness and generalization error bound), and a Monte--Carlo-based solution method of the proposed model are studied. The new model reveals the trade-off between the robustness to the unseen data and the specificity to the training data.

Distributional Robustness Bounds Generalization Errors

Bayesian methods, distributionally robust optimization methods, and regularization methods are three pillars of trustworthy machine learning hedging against distributional uncertainty, e.g., the uncertainty of an empirical distribution compared to the true underlying distribution. This paper investigates the connections among the three frameworks and, in particular, explores why these frameworks tend to have smaller generalization errors. Specifically, first, we suggest a quantitative definition for "distributional robustness", propose the concept of "robustness measure", and formalize several philosophical concepts in distributionally robust optimization. Second, we show that Bayesian methods are distributionally robust in the probably approximately correct (PAC) sense; In addition, by constructing a Dirichlet-process-like prior in Bayesian nonparametrics, it can be proven that any regularized empirical risk minimization method is equivalent to a Bayesian method. Third, we show that generalization errors of machine learning models can be characterized using the distributional uncertainty of the nominal distribution and the robustness measures of these machine learning models, which is a new perspective to bound generalization errors, and therefore, explain the reason why distributionally robust machine learning models, Bayesian models, and regularization models tend to have smaller generalization errors.

Robot Cooking with Stir-fry: Bimanual Non-prehensile Manipulation of Semi-fluid Objects

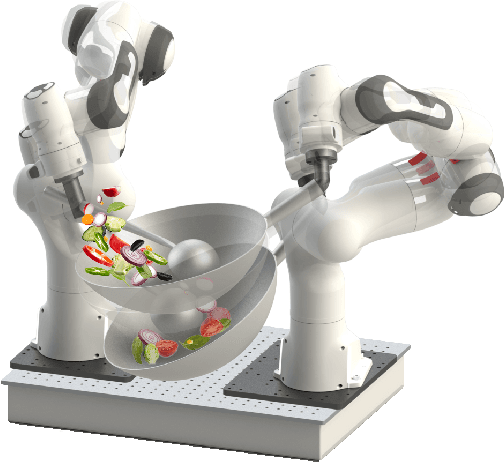
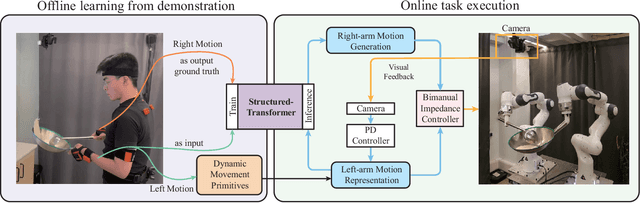
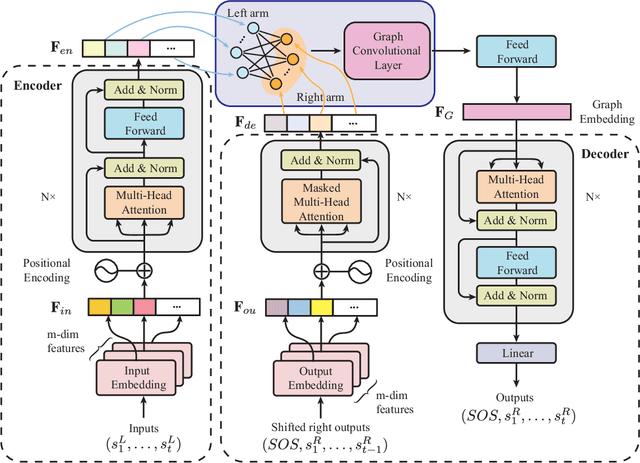
This letter describes an approach to achieve well-known Chinese cooking art stir-fry on a bimanual robot system. Stir-fry requires a sequence of highly dynamic coordinated movements, which is usually difficult to learn for a chef, let alone transfer to robots. In this letter, we define a canonical stir-fry movement, and then propose a decoupled framework for learning this deformable object manipulation from human demonstration. First, the dual arms of the robot are decoupled into different roles (a leader and follower) and learned with classical and neural network-based methods separately, then the bimanual task is transformed into a coordination problem. To obtain general bimanual coordination, we secondly propose a Graph and Transformer based model -- Structured-Transformer, to capture the spatio-temporal relationship between dual-arm movements. Finally, by adding visual feedback of content deformation, our framework can adjust the movements automatically to achieve the desired stir-fry effect. We verify the framework by a simulator and deploy it on a real bimanual Panda robot system. The experimental results validate our framework can realize the bimanual robot stir-fry motion and have the potential to extend to other deformable objects with bimanual coordination.