Mapping the Neuro-Symbolic AI Landscape by Architectures: A Handbook on Augmenting Deep Learning Through Symbolic Reasoning

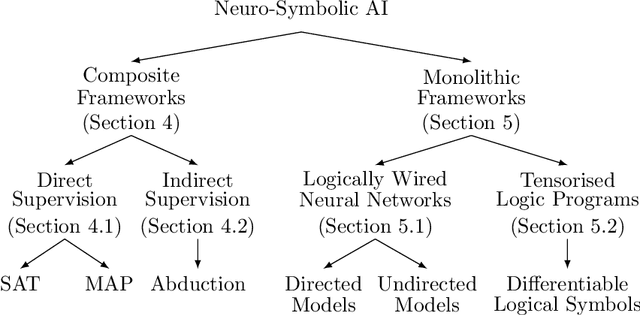
Integrating symbolic techniques with statistical ones is a long-standing problem in artificial intelligence. The motivation is that the strengths of either area match the weaknesses of the other, and $\unicode{x2013}$ by combining the two $\unicode{x2013}$ the weaknesses of either method can be limited. Neuro-symbolic AI focuses on this integration where the statistical methods are in particular neural networks. In recent years, there has been significant progress in this research field, where neuro-symbolic systems outperformed logical or neural models alone. Yet, neuro-symbolic AI is, comparatively speaking, still in its infancy and has not been widely adopted by machine learning practitioners. In this survey, we present the first mapping of neuro-symbolic techniques into families of frameworks based on their architectures, with several benefits: Firstly, it allows us to link different strengths of frameworks to their respective architectures. Secondly, it allows us to illustrate how engineers can augment their neural networks while treating the symbolic methods as black-boxes. Thirdly, it allows us to map most of the field so that future researchers can identify closely related frameworks.

Synthesising Recursive Functions for First-Order Model Counting: Challenges, Progress, and Conjectures

First-order model counting (FOMC) is a computational problem that asks to count the models of a sentence in finite-domain first-order logic. In this paper, we argue that the capabilities of FOMC algorithms to date are limited by their inability to express many types of recursive computations. To enable such computations, we relax the restrictions that typically accompany domain recursion and generalise the circuits used to express a solution to an FOMC problem to directed graphs that may contain cycles. To this end, we adapt the most well-established (weighted) FOMC algorithm ForcLift to work with such graphs and introduce new compilation rules that can create cycle-inducing edges that encode recursive function calls. These improvements allow the algorithm to find efficient solutions to counting problems that were previously beyond its reach, including those that cannot be solved efficiently by any other exact FOMC algorithm. We end with a few conjectures on what classes of instances could be domain-liftable as a result.

Generating Random Logic Programs Using Constraint Programming

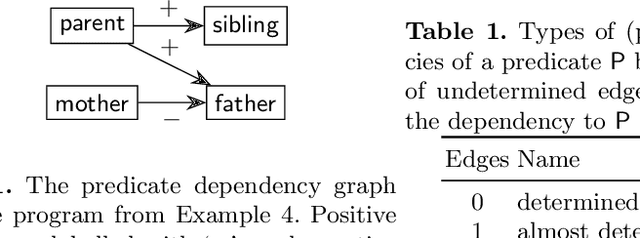
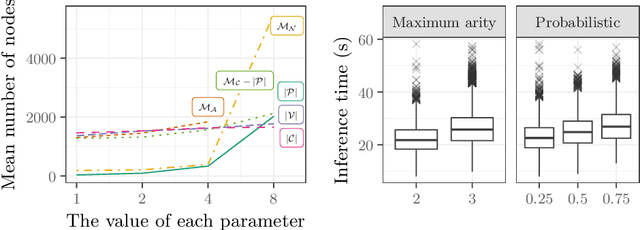
Testing algorithms across a wide range of problem instances is crucial to ensure the validity of any claim about one algorithm's superiority over another. However, when it comes to inference algorithms for probabilistic logic programs, experimental evaluations are limited to only a few programs. Existing methods to generate random logic programs are limited to propositional programs and often impose stringent syntactic restrictions. We present a novel approach to generating random logic programs and random probabilistic logic programs using constraint programming, introducing a new constraint to control the independence structure of the underlying probability distribution. We also provide a combinatorial argument for the correctness of the model, show how the model scales with parameter values, and use the model to compare probabilistic inference algorithms across a range of synthetic problems. Our model allows inference algorithm developers to evaluate and compare the algorithms across a wide range of instances, providing a detailed picture of their (comparative) strengths and weaknesses.