Mapping the Neuro-Symbolic AI Landscape by Architectures: A Handbook on Augmenting Deep Learning Through Symbolic Reasoning

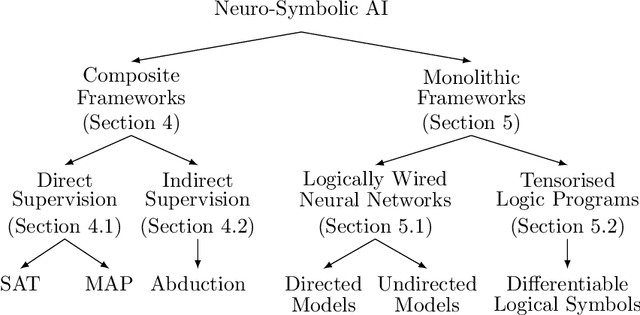
Integrating symbolic techniques with statistical ones is a long-standing problem in artificial intelligence. The motivation is that the strengths of either area match the weaknesses of the other, and $\unicode{x2013}$ by combining the two $\unicode{x2013}$ the weaknesses of either method can be limited. Neuro-symbolic AI focuses on this integration where the statistical methods are in particular neural networks. In recent years, there has been significant progress in this research field, where neuro-symbolic systems outperformed logical or neural models alone. Yet, neuro-symbolic AI is, comparatively speaking, still in its infancy and has not been widely adopted by machine learning practitioners. In this survey, we present the first mapping of neuro-symbolic techniques into families of frameworks based on their architectures, with several benefits: Firstly, it allows us to link different strengths of frameworks to their respective architectures. Secondly, it allows us to illustrate how engineers can augment their neural networks while treating the symbolic methods as black-boxes. Thirdly, it allows us to map most of the field so that future researchers can identify closely related frameworks.

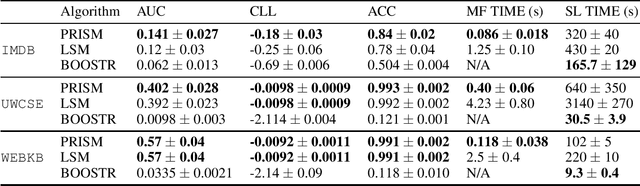
Efficiently Learning Probabilistic Logical Models by Cheaply Ranking Mined Rules

Probabilistic logical models are a core component of neurosymbolic AI and are important models in their own right for tasks that require high explainability. Unlike neural networks, logical models are often handcrafted using domain expertise, making their development costly and prone to errors. While there are algorithms that learn logical models from data, they are generally prohibitively expensive, limiting their applicability in real-world settings. In this work, we introduce precision and recall for logical rules and define their composition as rule utility -- a cost-effective measure to evaluate the predictive power of logical models. Further, we introduce SPECTRUM, a scalable framework for learning logical models from relational data. Its scalability derives from a linear-time algorithm that mines recurrent structures in the data along with a second algorithm that, using the cheap utility measure, efficiently ranks rules built from these structures. Moreover, we derive theoretical guarantees on the utility of the learnt logical model. As a result, SPECTRUM learns more accurate logical models orders of magnitude faster than previous methods on real-world datasets.

Parallel Neurosymbolic Integration with Concordia

Parallel neurosymbolic architectures have been applied effectively in NLP by distilling knowledge from a logic theory into a deep model.However, prior art faces several limitations including supporting restricted forms of logic theories and relying on the assumption of independence between the logic and the deep network. We present Concordia, a framework overcoming the limitations of prior art. Concordia is agnostic both to the deep network and the logic theory offering support for a wide range of probabilistic theories. Our framework can support supervised training of both components and unsupervised training of the neural component. Concordia has been successfully applied to tasks beyond NLP and data classification, improving the accuracy of state-of-the-art on collective activity detection, entity linking and recommendation tasks.

Principled and Efficient Motif Finding for Structure Learning in Lifted Graphical Models

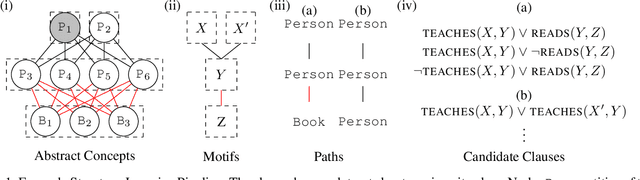
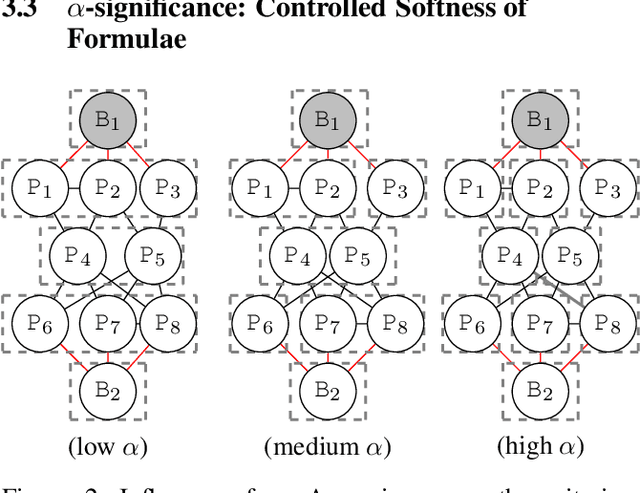
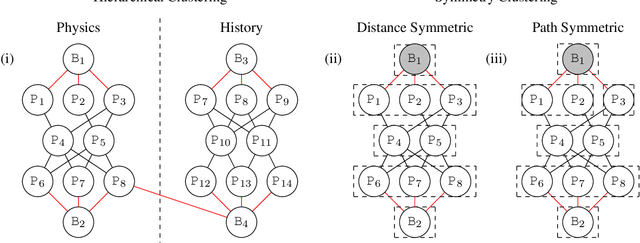
Structure learning is a core problem in AI central to the fields of neuro-symbolic AI and statistical relational learning. It consists in automatically learning a logical theory from data. The basis for structure learning is mining repeating patterns in the data, known as structural motifs. Finding these patterns reduces the exponential search space and therefore guides the learning of formulas. Despite the importance of motif learning, it is still not well understood. We present the first principled approach for mining structural motifs in lifted graphical models, languages that blend first-order logic with probabilistic models, which uses a stochastic process to measure the similarity of entities in the data. Our first contribution is an algorithm, which depends on two intuitive hyperparameters: one controlling the uncertainty in the entity similarity measure, and one controlling the softness of the resulting rules. Our second contribution is a preprocessing step where we perform hierarchical clustering on the data to reduce the search space to the most relevant data. Our third contribution is to introduce an O(n ln n) (in the size of the entities in the data) algorithm for clustering structurally-related data. We evaluate our approach using standard benchmarks and show that we outperform state-of-the-art structure learning approaches by up to 6% in terms of accuracy and up to 80% in terms of runtime.