Efthymia Tsamoura
On Improving Neurosymbolic Learning by Exploiting the Representation Space
Feb 08, 2026Abstract:We study the problem of learning neural classifiers in a neurosymbolic setting where the hidden gold labels of input instances must satisfy a logical formula. Learning in this setting proceeds by first computing (a subset of) the possible combinations of labels that satisfy the formula and then computing a loss using those combinations and the classifiers' scores. One challenge is that the space of label combinations can grow exponentially, making learning difficult. We propose a technique that prunes this space by exploiting the intuition that instances with similar latent representations are likely to share the same label. While this intuition has been widely used in weakly supervised learning, its application in our setting is challenging due to label dependencies imposed by logical constraints. We formulate the pruning process as an integer linear program that discards inconsistent label combinations while respecting logical structure. Our approach, CLIPPER, is orthogonal to existing training algorithms and can be seamlessly integrated with them. Across 16 benchmarks over complex neurosymbolic tasks, we demonstrate that CLIPPER boosts the performance of state-of-the-art neurosymbolic engines like Scallop, Dolphin, and ISED by up to 48%, 53%, and 8%, leading to state-of-the-art accuracies.
Symbol Grounding in Neuro-Symbolic AI: A Gentle Introduction to Reasoning Shortcuts
Oct 16, 2025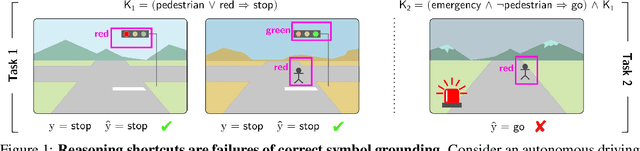

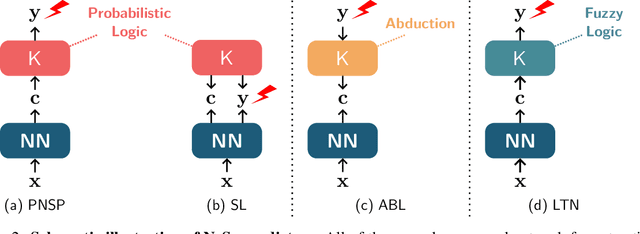
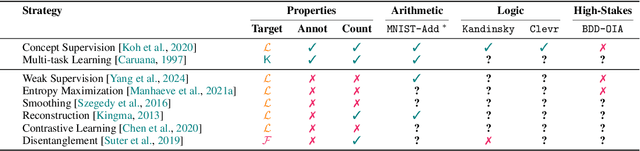
Abstract:Neuro-symbolic (NeSy) AI aims to develop deep neural networks whose predictions comply with prior knowledge encoding, e.g. safety or structural constraints. As such, it represents one of the most promising avenues for reliable and trustworthy AI. The core idea behind NeSy AI is to combine neural and symbolic steps: neural networks are typically responsible for mapping low-level inputs into high-level symbolic concepts, while symbolic reasoning infers predictions compatible with the extracted concepts and the prior knowledge. Despite their promise, it was recently shown that - whenever the concepts are not supervised directly - NeSy models can be affected by Reasoning Shortcuts (RSs). That is, they can achieve high label accuracy by grounding the concepts incorrectly. RSs can compromise the interpretability of the model's explanations, performance in out-of-distribution scenarios, and therefore reliability. At the same time, RSs are difficult to detect and prevent unless concept supervision is available, which is typically not the case. However, the literature on RSs is scattered, making it difficult for researchers and practitioners to understand and tackle this challenging problem. This overview addresses this issue by providing a gentle introduction to RSs, discussing their causes and consequences in intuitive terms. It also reviews and elucidates existing theoretical characterizations of this phenomenon. Finally, it details methods for dealing with RSs, including mitigation and awareness strategies, and maps their benefits and limitations. By reformulating advanced material in a digestible form, this overview aims to provide a unifying perspective on RSs to lower the bar to entry for tackling them. Ultimately, we hope this overview contributes to the development of reliable NeSy and trustworthy AI models.
Goal-Driven Query Answering over First- and Second-Order Dependencies with Equality
Dec 12, 2024



Abstract:Query answering over data with dependencies plays a central role in most applications of dependencies. The problem is commonly solved by using a suitable variant of the chase algorithm to compute a universal model of the dependencies and the data and thus explicate all knowledge implicit in the dependencies. After this preprocessing step, an arbitrary conjunctive query over the dependencies and the data can be answered by evaluating it the computed universal model. If, however, the query to be answered is fixed and known in advance, computing the universal model is often inefficient as many inferences made during this process can be irrelevant to a given query. In such cases, a goal-driven approach, which avoids drawing unnecessary inferences, promises to be more efficient and thus preferable in practice. In this paper we present what we believe to be the first technique for goal-driven query answering over first- and second-order dependencies with equality reasoning. Our technique transforms the input dependencies so that applying the chase to the output avoids many inferences that are irrelevant to the query. The transformation proceeds in several steps, which comprise the following three novel techniques. First, we present a variant of the singularisation technique by Marnette [60] that is applicable to second-order dependencies and that corrects an incompleteness of a related formulation by ten Cate et al. [74]. Second, we present a relevance analysis technique that can eliminate from the input dependencies that provably do not contribute to query answers. Third, we present a variant of the magic sets algorithm [19] that can handle second-order dependencies with equality reasoning. We also present the results of an extensive empirical evaluation, which show that goal-driven query answering can be orders of magnitude faster than computing the full universal model.
Mapping the Neuro-Symbolic AI Landscape by Architectures: A Handbook on Augmenting Deep Learning Through Symbolic Reasoning
Oct 29, 2024
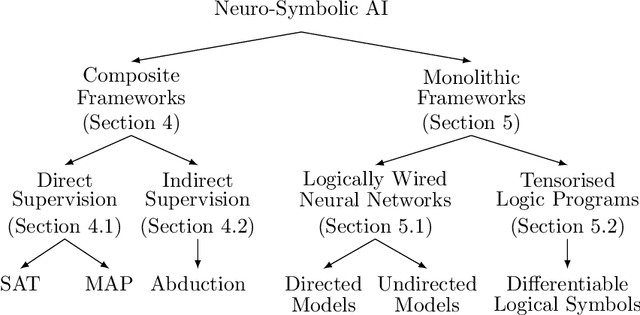

Abstract:Integrating symbolic techniques with statistical ones is a long-standing problem in artificial intelligence. The motivation is that the strengths of either area match the weaknesses of the other, and $\unicode{x2013}$ by combining the two $\unicode{x2013}$ the weaknesses of either method can be limited. Neuro-symbolic AI focuses on this integration where the statistical methods are in particular neural networks. In recent years, there has been significant progress in this research field, where neuro-symbolic systems outperformed logical or neural models alone. Yet, neuro-symbolic AI is, comparatively speaking, still in its infancy and has not been widely adopted by machine learning practitioners. In this survey, we present the first mapping of neuro-symbolic techniques into families of frameworks based on their architectures, with several benefits: Firstly, it allows us to link different strengths of frameworks to their respective architectures. Secondly, it allows us to illustrate how engineers can augment their neural networks while treating the symbolic methods as black-boxes. Thirdly, it allows us to map most of the field so that future researchers can identify closely related frameworks.
Efficiently Learning Probabilistic Logical Models by Cheaply Ranking Mined Rules
Sep 24, 2024Abstract:Probabilistic logical models are a core component of neurosymbolic AI and are important models in their own right for tasks that require high explainability. Unlike neural networks, logical models are often handcrafted using domain expertise, making their development costly and prone to errors. While there are algorithms that learn logical models from data, they are generally prohibitively expensive, limiting their applicability in real-world settings. In this work, we introduce precision and recall for logical rules and define their composition as rule utility -- a cost-effective measure to evaluate the predictive power of logical models. Further, we introduce SPECTRUM, a scalable framework for learning logical models from relational data. Its scalability derives from a linear-time algorithm that mines recurrent structures in the data along with a second algorithm that, using the cheap utility measure, efficiently ranks rules built from these structures. Moreover, we derive theoretical guarantees on the utility of the learnt logical model. As a result, SPECTRUM learns more accurate logical models orders of magnitude faster than previous methods on real-world datasets.
On Characterizing and Mitigating Imbalances in Multi-Instance Partial Label Learning
Jul 13, 2024Abstract:Multi-Instance Partial Label Learning (MI-PLL) is a weakly-supervised learning setting encompassing partial label learning, latent structural learning, and neurosymbolic learning. Differently from supervised learning, in MI-PLL, the inputs to the classifiers at training-time are tuples of instances $\textbf{x}$, while the supervision signal is generated by a function $\sigma$ over the gold labels of $\textbf{x}$. The gold labels are hidden during training. In this paper, we focus on characterizing and mitigating learning imbalances, i.e., differences in the errors occurring when classifying instances of different classes (aka class-specific risks), under MI-PLL. The phenomenon of learning imbalances has been extensively studied in the context of long-tail learning; however, the nature of MI-PLL introduces new challenges. Our contributions are as follows. From a theoretical perspective, we characterize the learning imbalances by deriving class-specific risk bounds that depend upon the function $\sigma$. Our theory reveals that learning imbalances exist in MI-PLL even when the hidden labels are uniformly distributed. On the practical side, we introduce a technique for estimating the marginal of the hidden labels using only MI-PLL data. Then, we introduce algorithms that mitigate imbalances at training- and testing-time, by treating the marginal of the hidden labels as a constraint. The first algorithm relies on a novel linear programming formulation of MI-PLL for pseudo-labeling. The second one adjusts a model's scores based on robust optimal transport. We demonstrate the effectiveness of our techniques using strong neurosymbolic and long-tail learning baselines, discussing also open challenges.
Parallel Neurosymbolic Integration with Concordia
Jun 14, 2023



Abstract:Parallel neurosymbolic architectures have been applied effectively in NLP by distilling knowledge from a logic theory into a deep model.However, prior art faces several limitations including supporting restricted forms of logic theories and relying on the assumption of independence between the logic and the deep network. We present Concordia, a framework overcoming the limitations of prior art. Concordia is agnostic both to the deep network and the logic theory offering support for a wide range of probabilistic theories. Our framework can support supervised training of both components and unsupervised training of the neural component. Concordia has been successfully applied to tasks beyond NLP and data classification, improving the accuracy of state-of-the-art on collective activity detection, entity linking and recommendation tasks.
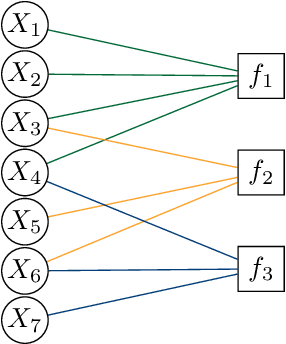
Principled and Efficient Motif Finding for Structure Learning in Lifted Graphical Models
Feb 09, 2023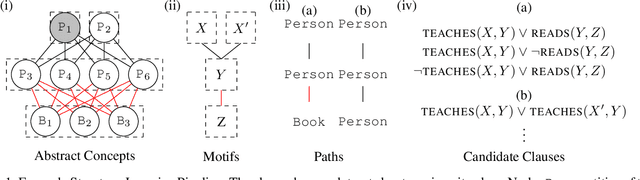
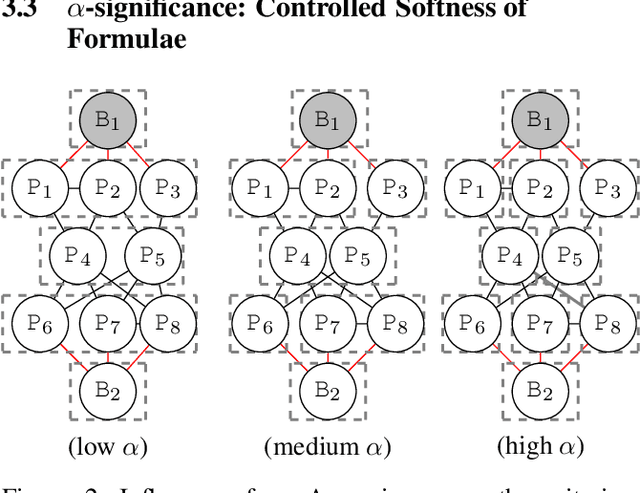
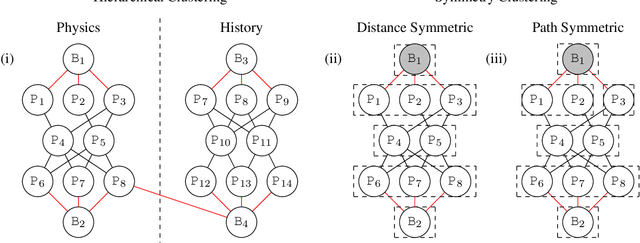
Abstract:Structure learning is a core problem in AI central to the fields of neuro-symbolic AI and statistical relational learning. It consists in automatically learning a logical theory from data. The basis for structure learning is mining repeating patterns in the data, known as structural motifs. Finding these patterns reduces the exponential search space and therefore guides the learning of formulas. Despite the importance of motif learning, it is still not well understood. We present the first principled approach for mining structural motifs in lifted graphical models, languages that blend first-order logic with probabilistic models, which uses a stochastic process to measure the similarity of entities in the data. Our first contribution is an algorithm, which depends on two intuitive hyperparameters: one controlling the uncertainty in the entity similarity measure, and one controlling the softness of the resulting rules. Our second contribution is a preprocessing step where we perform hierarchical clustering on the data to reduce the search space to the most relevant data. Our third contribution is to introduce an O(n ln n) (in the size of the entities in the data) algorithm for clustering structurally-related data. We evaluate our approach using standard benchmarks and show that we outperform state-of-the-art structure learning approaches by up to 6% in terms of accuracy and up to 80% in terms of runtime.
Scalable Regularization of Scene Graph Generation Models using Symbolic Theories
Sep 06, 2022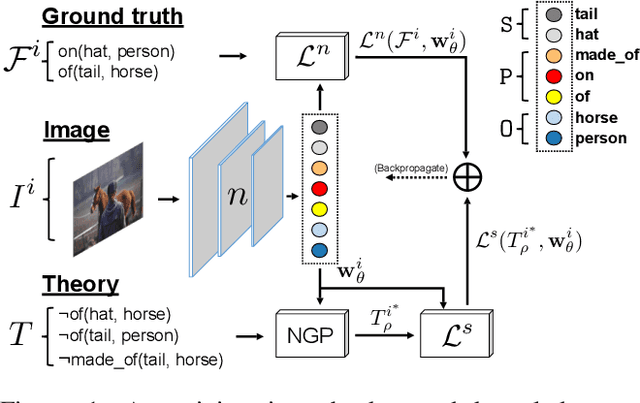

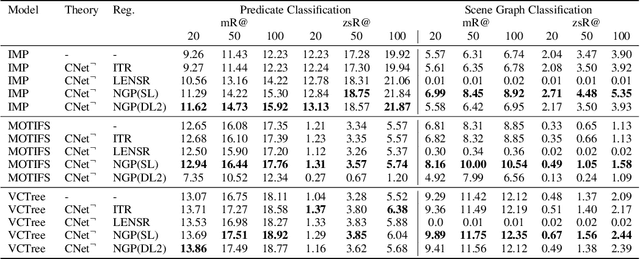

Abstract:Several techniques have recently aimed to improve the performance of deep learning models for Scene Graph Generation (SGG) by incorporating background knowledge. State-of-the-art techniques can be divided into two families: one where the background knowledge is incorporated into the model in a subsymbolic fashion, and another in which the background knowledge is maintained in symbolic form. Despite promising results, both families of techniques face several shortcomings: the first one requires ad-hoc, more complex neural architectures increasing the training or inference cost; the second one suffers from limited scalability w.r.t. the size of the background knowledge. Our work introduces a regularization technique for injecting symbolic background knowledge into neural SGG models that overcomes the limitations of prior art. Our technique is model-agnostic, does not incur any cost at inference time, and scales to previously unmanageable background knowledge sizes. We demonstrate that our technique can improve the accuracy of state-of-the-art SGG models, by up to 33%.
Materializing Knowledge Bases via Trigger Graphs
Feb 04, 2021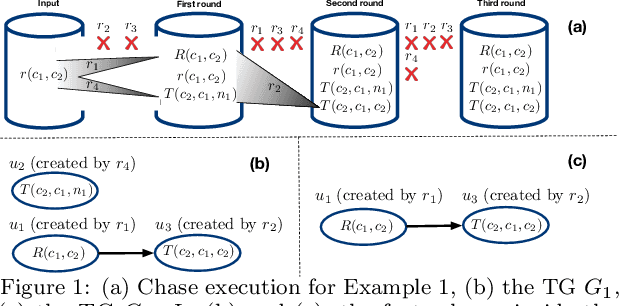
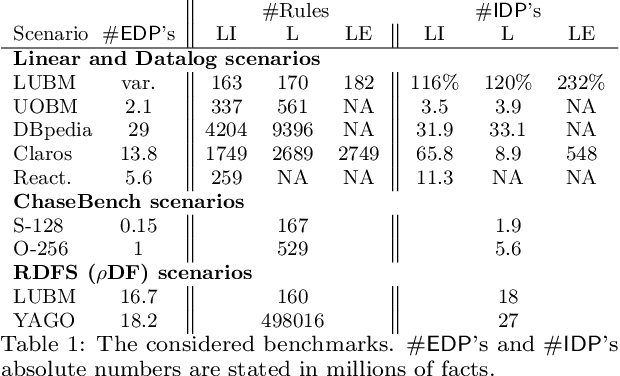
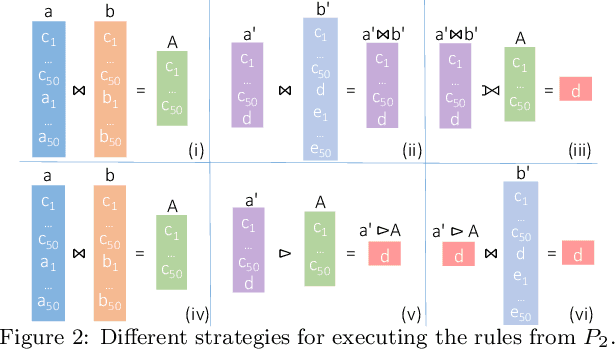
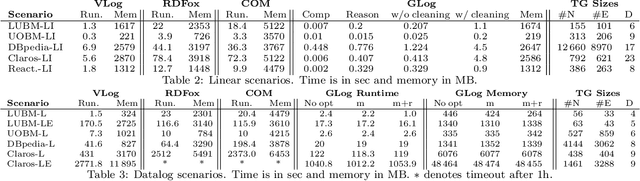
Abstract:The chase is a well-established family of algorithms used to materialize Knowledge Bases (KBs), like Knowledge Graphs (KGs), to tackle important tasks like query answering under dependencies or data cleaning. A general problem of chase algorithms is that they might perform redundant computations. To counter this problem, we introduce the notion of Trigger Graphs (TGs), which guide the execution of the rules avoiding redundant computations. We present the results of an extensive theoretical and empirical study that seeks to answer when and how TGs can be computed and what are the benefits of TGs when applied over real-world KBs. Our results include introducing algorithms that compute (minimal) TGs. We implemented our approach in a new engine, and our experiments show that it can be significantly more efficient than the chase enabling us to materialize KBs with 17B facts in less than 40 min on commodity machines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge