On the Complexity of Global Necessary Reasons to Explain Classification

Explainable AI has garnered considerable attention in recent years, as understanding the reasons behind decisions or predictions made by AI systems is crucial for their successful adoption. Explaining classifiers' behavior is one prominent problem. Work in this area has proposed notions of both local and global explanations, where the former are concerned with explaining a classifier's behavior for a specific instance, while the latter are concerned with explaining the overall classifier's behavior regardless of any specific instance. In this paper, we focus on global explanations, and explain classification in terms of ``minimal'' necessary conditions for the classifier to assign a specific class to a generic instance. We carry out a thorough complexity analysis of the problem for natural minimality criteria and important families of classifiers considered in the literature.

Materializing Knowledge Bases via Trigger Graphs

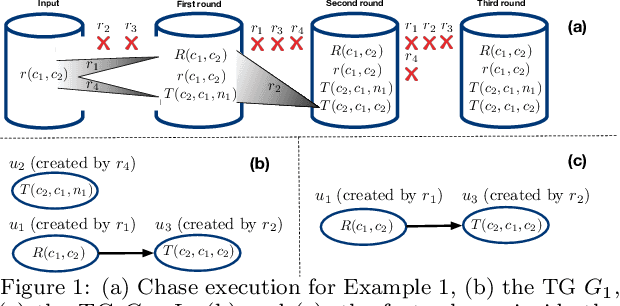
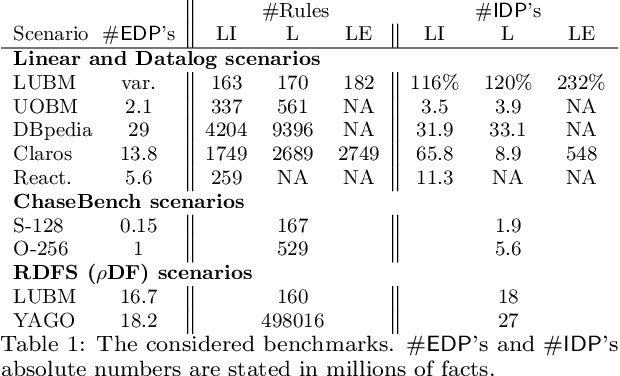
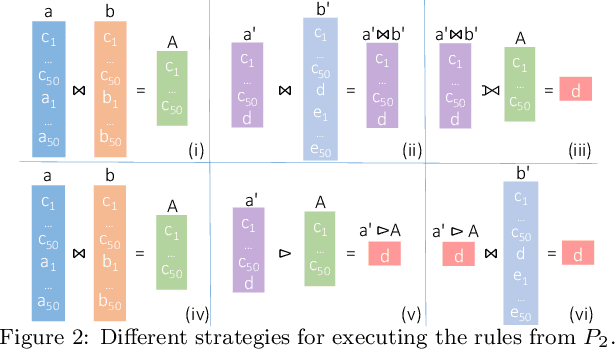
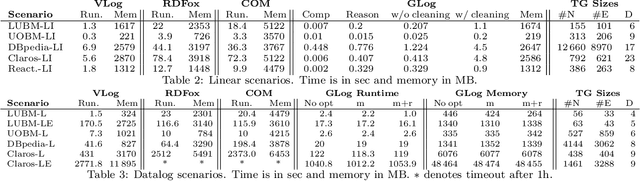
The chase is a well-established family of algorithms used to materialize Knowledge Bases (KBs), like Knowledge Graphs (KGs), to tackle important tasks like query answering under dependencies or data cleaning. A general problem of chase algorithms is that they might perform redundant computations. To counter this problem, we introduce the notion of Trigger Graphs (TGs), which guide the execution of the rules avoiding redundant computations. We present the results of an extensive theoretical and empirical study that seeks to answer when and how TGs can be computed and what are the benefits of TGs when applied over real-world KBs. Our results include introducing algorithms that compute (minimal) TGs. We implemented our approach in a new engine, and our experiments show that it can be significantly more efficient than the chase enabling us to materialize KBs with 17B facts in less than 40 min on commodity machines.

Complexity Results for Preference Aggregation over (m)CP-nets: Pareto and Majority Voting

Combinatorial preference aggregation has many applications in AI. Given the exponential nature of these preferences, compact representations are needed and ($m$)CP-nets are among the most studied ones. Sequential and global voting are two ways to aggregate preferences over CP-nets. In the former, preferences are aggregated feature-by-feature. Hence, when preferences have specific feature dependencies, sequential voting may exhibit voting paradoxes, i.e., it might select sub-optimal outcomes. To avoid paradoxes in sequential voting, one has often assumed the $\mathcal{O}$-legality restriction, which imposes a shared topological order among all the CP-nets. On the contrary, in global voting, CP-nets are considered as a whole during preference aggregation. For this reason, global voting is immune from paradoxes, and there is no need to impose restrictions over the CP-nets' topological structure. Sequential voting over $\mathcal{O}$-legal CP-nets has extensively been investigated. On the other hand, global voting over non-$\mathcal{O}$-legal CP-nets has not carefully been analyzed, despite it was stated in the literature that a theoretical comparison between global and sequential voting was promising and a precise complexity analysis for global voting has been asked for multiple times. In quite few works, very partial results on the complexity of global voting over CP-nets have been given. We start to fill this gap by carrying out a thorough complexity analysis of Pareto and majority global voting over not necessarily $\mathcal{O}$-legal acyclic binary polynomially connected (m)CP-nets. We settle these problems in the polynomial hierarchy, and some of them in PTIME or LOGSPACE, whereas EXPTIME was the previously known upper bound for most of them. We show various tight lower bounds and matching upper bounds for problems that up to date did not have any explicit non-obvious lower bound.

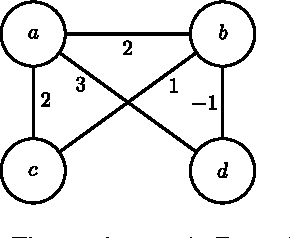
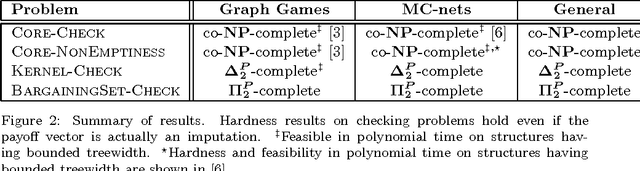
On the Complexity of Core, Kernel, and Bargaining Set

Coalitional games are mathematical models suited to analyze scenarios where players can collaborate by forming coalitions in order to obtain higher worths than by acting in isolation. A fundamental problem for coalitional games is to single out the most desirable outcomes in terms of appropriate notions of worth distributions, which are usually called solution concepts. Motivated by the fact that decisions taken by realistic players cannot involve unbounded resources, recent computer science literature reconsidered the definition of such concepts by advocating the relevance of assessing the amount of resources needed for their computation in terms of their computational complexity. By following this avenue of research, the paper provides a complete picture of the complexity issues arising with three prominent solution concepts for coalitional games with transferable utility, namely, the core, the kernel, and the bargaining set, whenever the game worth-function is represented in some reasonable compact form (otherwise, if the worths of all coalitions are explicitly listed, the input sizes are so large that complexity problems are---artificially---trivial). The starting investigation point is the setting of graph games, about which various open questions were stated in the literature. The paper gives an answer to these questions, and in addition provides new insights on the setting, by characterizing the computational complexity of the three concepts in some relevant generalizations and specializations.