The Complexity of Why-Provenance for Datalog Queries

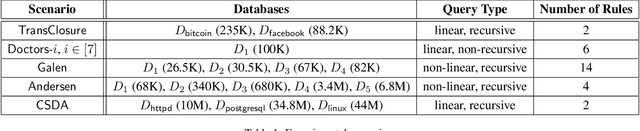
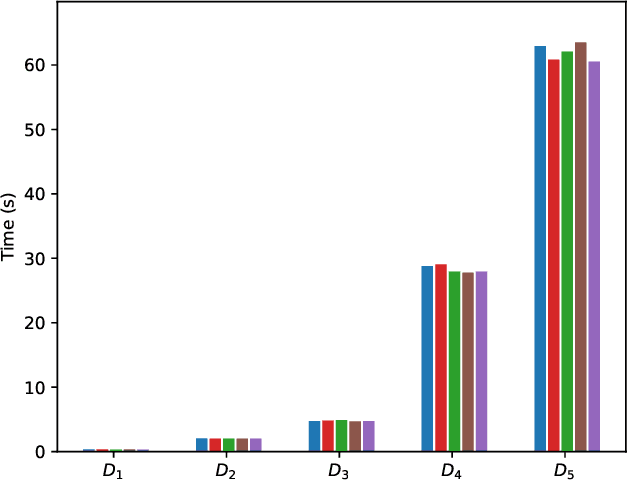
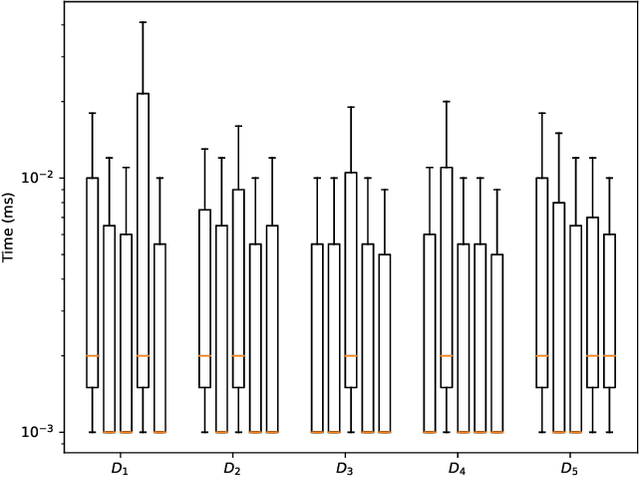
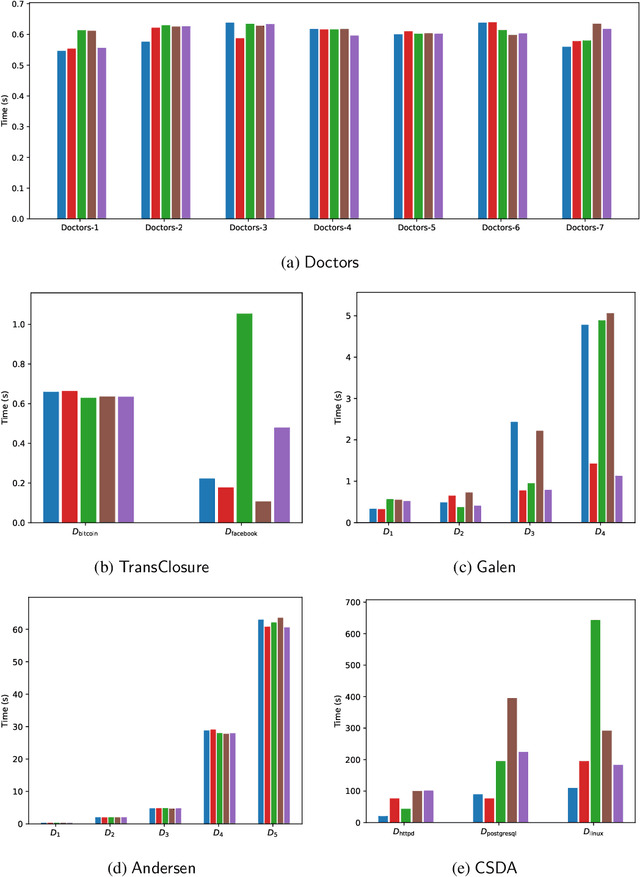
Explaining why a database query result is obtained is an essential task towards the goal of Explainable AI, especially nowadays where expressive database query languages such as Datalog play a critical role in the development of ontology-based applications. A standard way of explaining a query result is the so-called why-provenance, which essentially provides information about the witnesses to a query result in the form of subsets of the input database that are sufficient to derive that result. To our surprise, despite the fact that the notion of why-provenance for Datalog queries has been around for decades and intensively studied, its computational complexity remains unexplored. The goal of this work is to fill this apparent gap in the why-provenance literature. Towards this end, we pinpoint the data complexity of why-provenance for Datalog queries and key subclasses thereof. The takeaway of our work is that why-provenance for recursive queries, even if the recursion is limited to be linear, is an intractable problem, whereas for non-recursive queries is highly tractable. Having said that, we experimentally confirm, by exploiting SAT solvers, that making why-provenance for (recursive) Datalog queries work in practice is not an unrealistic goal.

Semi-Oblivious Chase Termination for Linear Existential Rules: An Experimental Study

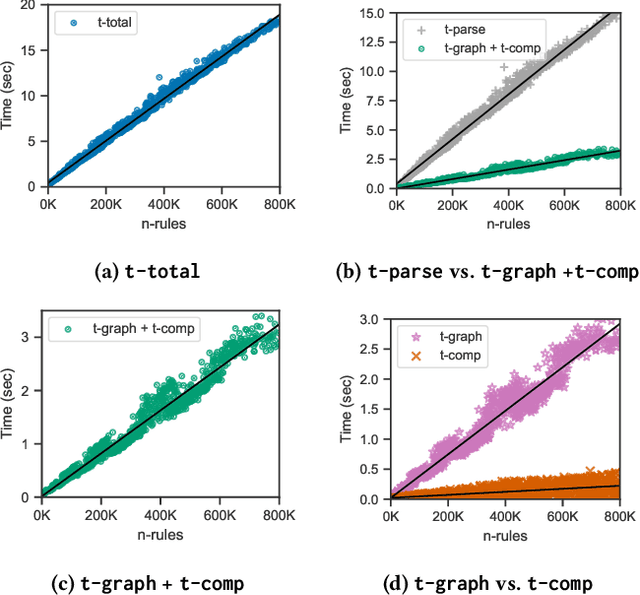
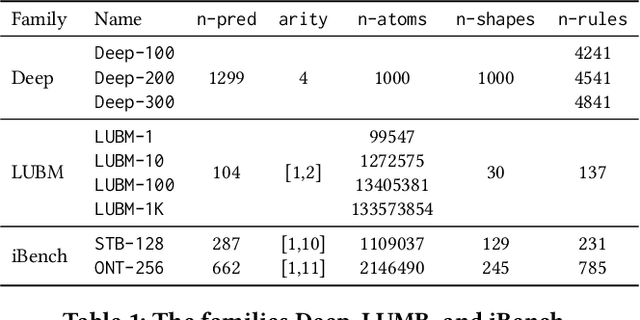
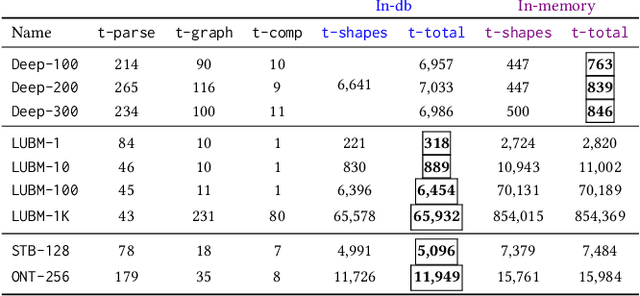
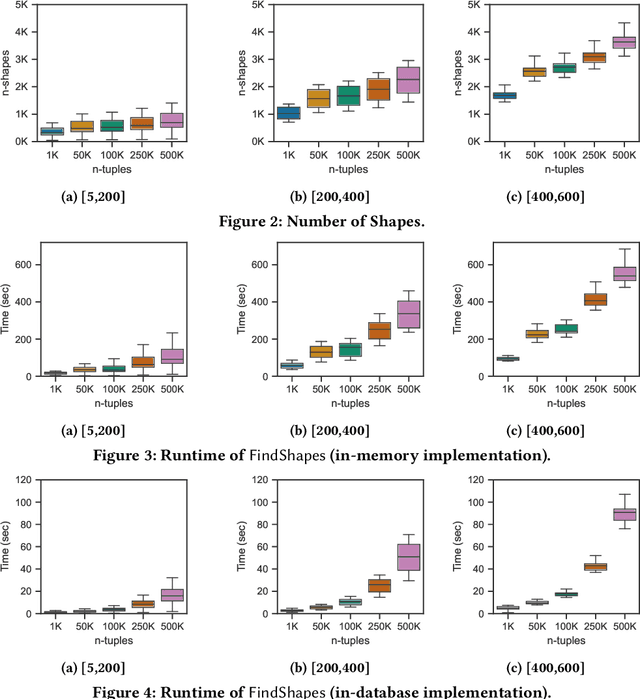
The chase procedure is a fundamental algorithmic tool in databases that allows us to reason with constraints, such as existential rules, with a plethora of applications. It takes as input a database and a set of constraints, and iteratively completes the database as dictated by the constraints. A key challenge, though, is the fact that it may not terminate, which leads to the problem of checking whether it terminates given a database and a set of constraints. In this work, we focus on the semi-oblivious version of the chase, which is well-suited for practical implementations, and linear existential rules, a central class of constraints with several applications. In this setting, there is a mature body of theoretical work that provides syntactic characterizations of when the chase terminates, algorithms for checking chase termination, precise complexity results, and worst-case optimal bounds on the size of the result of the chase (whenever is finite). Our main objective is to experimentally evaluate the existing chase termination algorithms with the aim of understanding which input parameters affect their performance, clarifying whether they can be used in practice, and revealing their performance limitations.

Non-Uniformly Terminating Chase: Size and Complexity

The chase procedure, originally introduced for checking implication of database constraints, and later on used for computing data exchange solutions, has recently become a central algorithmic tool in rule-based ontological reasoning. In this context, a key problem is non-uniform chase termination: does the chase of a database w.r.t. a rule-based ontology terminate? And if this is the case, what is the size of the result of the chase? We focus on guarded tuple-generating dependencies (TGDs), which form a robust rule-based ontology language, and study the above central questions for the semi-oblivious version of the chase. One of our main findings is that non-uniform semi-oblivious chase termination for guarded TGDs is feasible in polynomial time w.r.t. the database, and the size of the result of the chase (whenever is finite) is linear w.r.t. the database. Towards our results concerning non-uniform chase termination, we show that basic techniques such as simplification and linearization, originally introduced in the context of ontological query answering, can be safely applied to the chase termination problem.

Using Linear Constraints for Logic Program Termination Analysis

It is widely acknowledged that function symbols are an important feature in answer set programming, as they make modeling easier, increase the expressive power, and allow us to deal with infinite domains. The main issue with their introduction is that the evaluation of a program might not terminate and checking whether it terminates or not is undecidable. To cope with this problem, several classes of logic programs have been proposed where the use of function symbols is restricted but the program evaluation termination is guaranteed. Despite the significant body of work in this area, current approaches do not include many simple practical programs whose evaluation terminates. In this paper, we present the novel classes of rule-bounded and cycle-bounded programs, which overcome different limitations of current approaches by performing a more global analysis of how terms are propagated from the body to the head of rules. Results on the correctness, the complexity, and the expressivity of the proposed approach are provided.