The Complexity of Why-Provenance for Datalog Queries

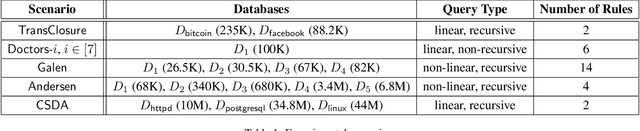
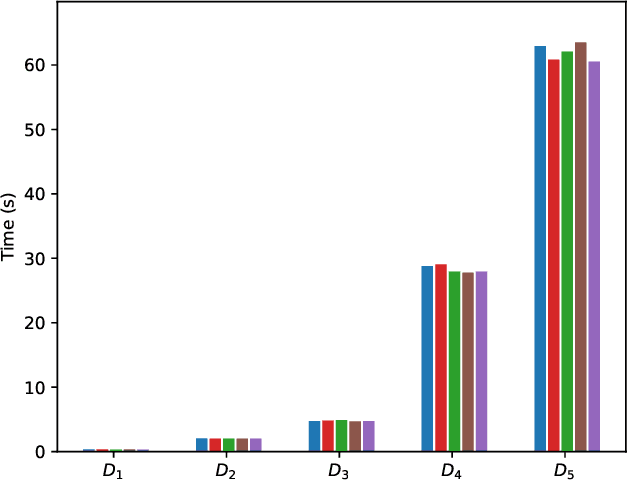
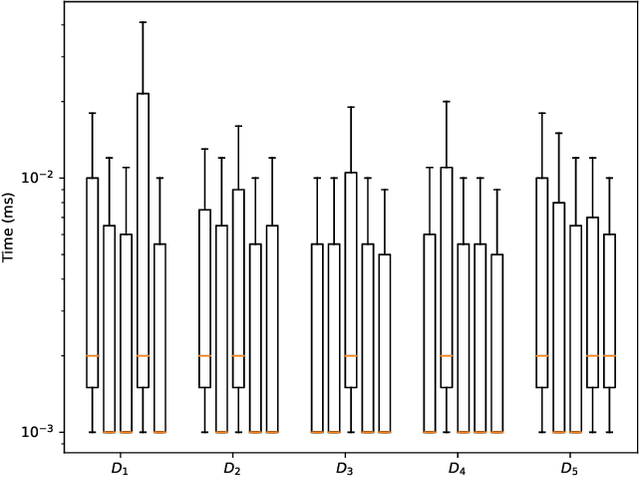
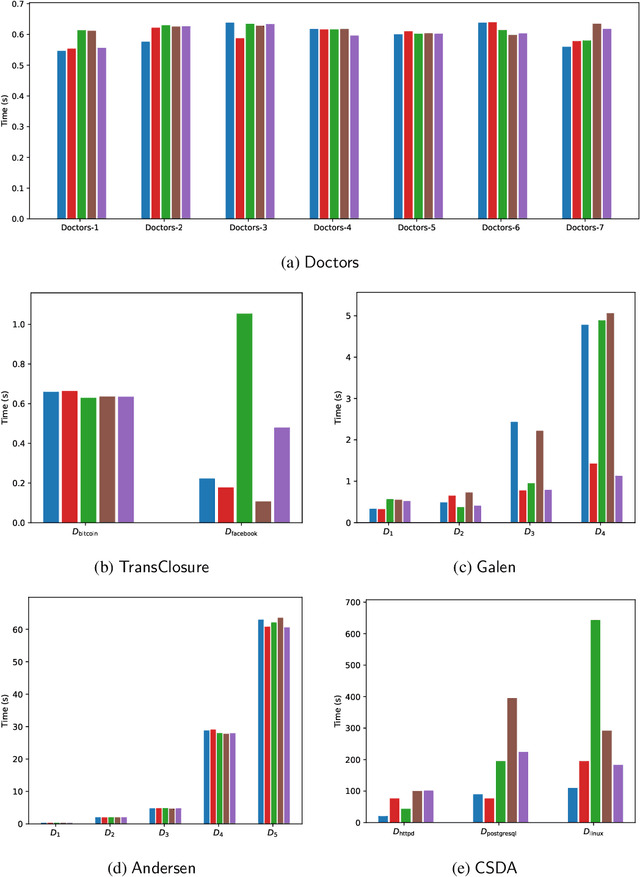
Explaining why a database query result is obtained is an essential task towards the goal of Explainable AI, especially nowadays where expressive database query languages such as Datalog play a critical role in the development of ontology-based applications. A standard way of explaining a query result is the so-called why-provenance, which essentially provides information about the witnesses to a query result in the form of subsets of the input database that are sufficient to derive that result. To our surprise, despite the fact that the notion of why-provenance for Datalog queries has been around for decades and intensively studied, its computational complexity remains unexplored. The goal of this work is to fill this apparent gap in the why-provenance literature. Towards this end, we pinpoint the data complexity of why-provenance for Datalog queries and key subclasses thereof. The takeaway of our work is that why-provenance for recursive queries, even if the recursion is limited to be linear, is an intractable problem, whereas for non-recursive queries is highly tractable. Having said that, we experimentally confirm, by exploiting SAT solvers, that making why-provenance for (recursive) Datalog queries work in practice is not an unrealistic goal.

Expected Similarity Estimation for Large-Scale Batch and Streaming Anomaly Detection

We present a novel algorithm for anomaly detection on very large datasets and data streams. The method, named EXPected Similarity Estimation (EXPoSE), is kernel-based and able to efficiently compute the similarity between new data points and the distribution of regular data. The estimator is formulated as an inner product with a reproducing kernel Hilbert space embedding and makes no assumption about the type or shape of the underlying data distribution. We show that offline (batch) learning with EXPoSE can be done in linear time and online (incremental) learning takes constant time per instance and model update. Furthermore, EXPoSE can make predictions in constant time, while it requires only constant memory. In addition, we propose different methodologies for concept drift adaptation on evolving data streams. On several real datasets we demonstrate that our approach can compete with state of the art algorithms for anomaly detection while being an order of magnitude faster than most other approaches.

Constant Time EXPected Similarity Estimation using Stochastic Optimization

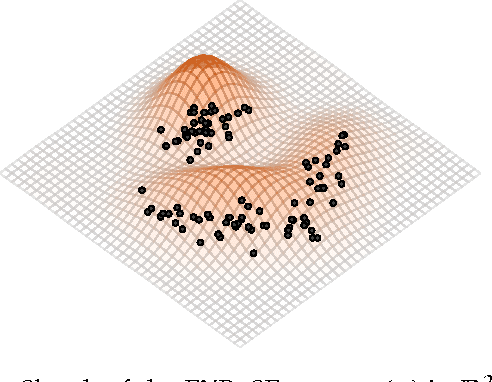
A new algorithm named EXPected Similarity Estimation (EXPoSE) was recently proposed to solve the problem of large-scale anomaly detection. It is a non-parametric and distribution free kernel method based on the Hilbert space embedding of probability measures. Given a dataset of $n$ samples, EXPoSE needs only $\mathcal{O}(n)$ (linear time) to build a model and $\mathcal{O}(1)$ (constant time) to make a prediction. In this work we improve the linear computational complexity and show that an $\epsilon$-accurate model can be estimated in constant time, which has significant implications for large-scale learning problems. To achieve this goal, we cast the original EXPoSE formulation into a stochastic optimization problem. It is crucial that this approach allows us to determine the number of iteration based on a desired accuracy $\epsilon$, independent of the dataset size $n$. We will show that the proposed stochastic gradient descent algorithm works in general (possible infinite-dimensional) Hilbert spaces, is easy to implement and requires no additional step-size parameters.

Transductive Learning for Multi-Task Copula Processes

We tackle the problem of multi-task learning with copula process. Multivariable prediction in spatial and spatial-temporal processes such as natural resource estimation and pollution monitoring have been typically addressed using techniques based on Gaussian processes and co-Kriging. While the Gaussian prior assumption is convenient from analytical and computational perspectives, nature is dominated by non-Gaussian likelihoods. Copula processes are an elegant and flexible solution to handle various non-Gaussian likelihoods by capturing the dependence structure of random variables with cumulative distribution functions rather than their marginals. We show how multi-task learning for copula processes can be used to improve multivariable prediction for problems where the simple Gaussianity prior assumption does not hold. Then, we present a transductive approximation for multi-task learning and derive analytical expressions for the copula process model. The approach is evaluated and compared to other techniques in one artificial dataset and two publicly available datasets for natural resource estimation and concrete slump prediction.