Efficient Dictionary Learning with Sparseness-Enforcing Projections

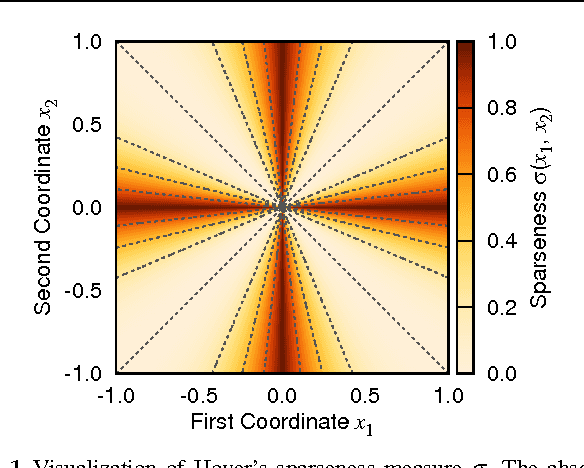
Learning dictionaries suitable for sparse coding instead of using engineered bases has proven effective in a variety of image processing tasks. This paper studies the optimization of dictionaries on image data where the representation is enforced to be explicitly sparse with respect to a smooth, normalized sparseness measure. This involves the computation of Euclidean projections onto level sets of the sparseness measure. While previous algorithms for this optimization problem had at least quasi-linear time complexity, here the first algorithm with linear time complexity and constant space complexity is proposed. The key for this is the mathematically rigorous derivation of a characterization of the projection's result based on a soft-shrinkage function. This theory is applied in an original algorithm called Easy Dictionary Learning (EZDL), which learns dictionaries with a simple and fast-to-compute Hebbian-like learning rule. The new algorithm is efficient, expressive and particularly simple to implement. It is demonstrated that despite its simplicity, the proposed learning algorithm is able to generate a rich variety of dictionaries, in particular a topographic organization of atoms or separable atoms. Further, the dictionaries are as expressive as those of benchmark learning algorithms in terms of the reproduction quality on entire images, and result in an equivalent denoising performance. EZDL learns approximately 30 % faster than the already very efficient Online Dictionary Learning algorithm, and is therefore eligible for rapid data set analysis and problems with vast quantities of learning samples.

Sparse Activity and Sparse Connectivity in Supervised Learning

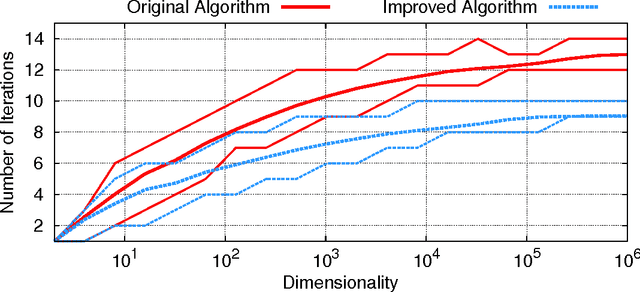
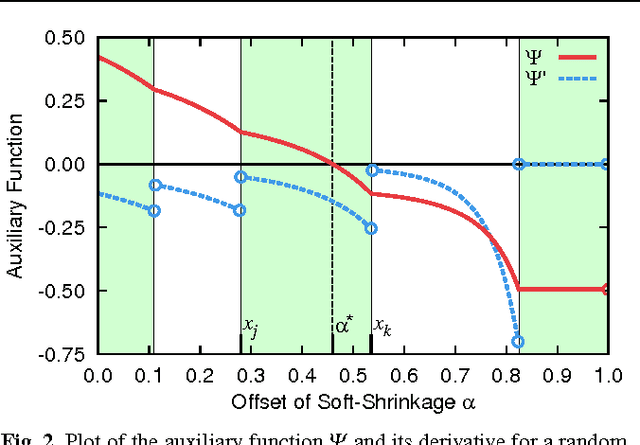
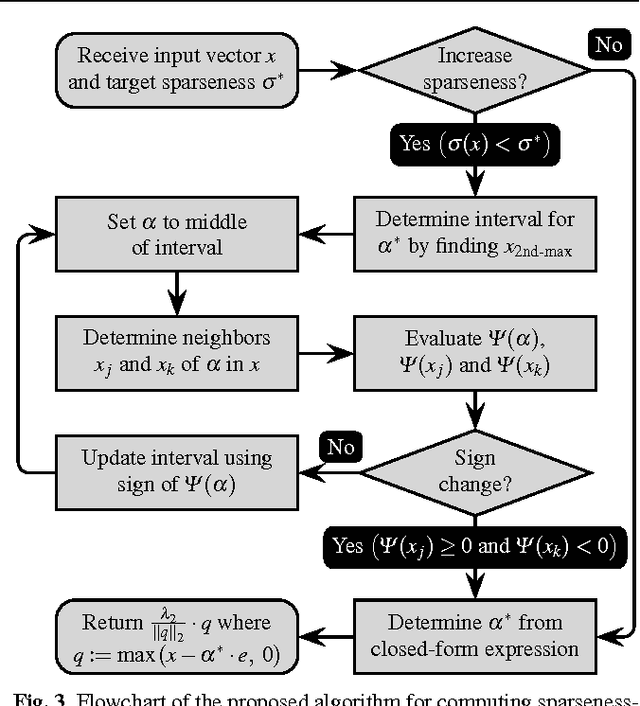
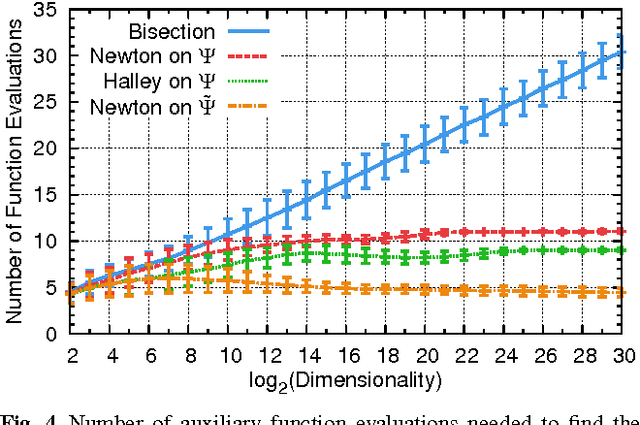
Sparseness is a useful regularizer for learning in a wide range of applications, in particular in neural networks. This paper proposes a model targeted at classification tasks, where sparse activity and sparse connectivity are used to enhance classification capabilities. The tool for achieving this is a sparseness-enforcing projection operator which finds the closest vector with a pre-defined sparseness for any given vector. In the theoretical part of this paper, a comprehensive theory for such a projection is developed. In conclusion, it is shown that the projection is differentiable almost everywhere and can thus be implemented as a smooth neuronal transfer function. The entire model can hence be tuned end-to-end using gradient-based methods. Experiments on the MNIST database of handwritten digits show that classification performance can be boosted by sparse activity or sparse connectivity. With a combination of both, performance can be significantly better compared to classical non-sparse approaches.

Constant Time EXPected Similarity Estimation using Stochastic Optimization

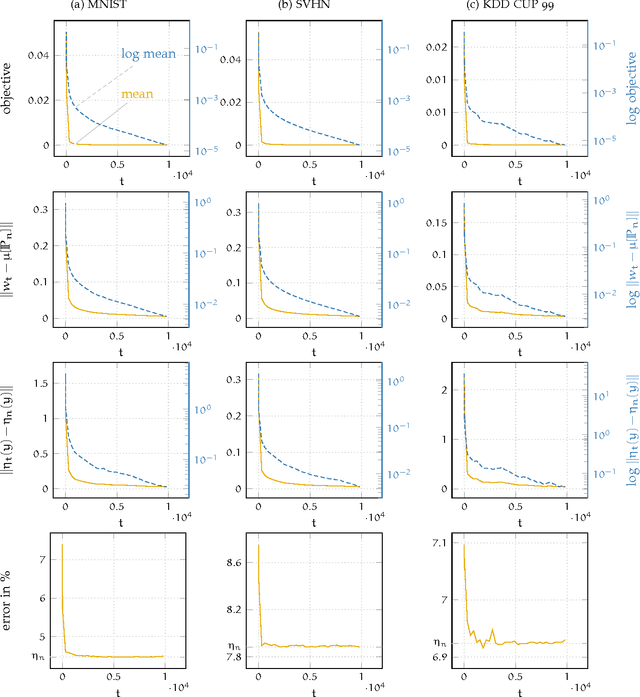
A new algorithm named EXPected Similarity Estimation (EXPoSE) was recently proposed to solve the problem of large-scale anomaly detection. It is a non-parametric and distribution free kernel method based on the Hilbert space embedding of probability measures. Given a dataset of $n$ samples, EXPoSE needs only $\mathcal{O}(n)$ (linear time) to build a model and $\mathcal{O}(1)$ (constant time) to make a prediction. In this work we improve the linear computational complexity and show that an $\epsilon$-accurate model can be estimated in constant time, which has significant implications for large-scale learning problems. To achieve this goal, we cast the original EXPoSE formulation into a stochastic optimization problem. It is crucial that this approach allows us to determine the number of iteration based on a desired accuracy $\epsilon$, independent of the dataset size $n$. We will show that the proposed stochastic gradient descent algorithm works in general (possible infinite-dimensional) Hilbert spaces, is easy to implement and requires no additional step-size parameters.