Constant Time EXPected Similarity Estimation using Stochastic Optimization
Paper and Code
Nov 17, 2015
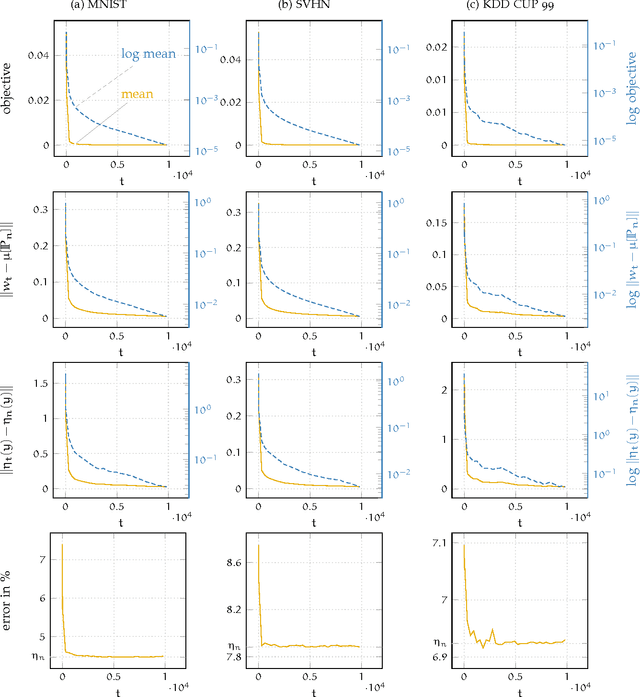
A new algorithm named EXPected Similarity Estimation (EXPoSE) was recently proposed to solve the problem of large-scale anomaly detection. It is a non-parametric and distribution free kernel method based on the Hilbert space embedding of probability measures. Given a dataset of $n$ samples, EXPoSE needs only $\mathcal{O}(n)$ (linear time) to build a model and $\mathcal{O}(1)$ (constant time) to make a prediction. In this work we improve the linear computational complexity and show that an $\epsilon$-accurate model can be estimated in constant time, which has significant implications for large-scale learning problems. To achieve this goal, we cast the original EXPoSE formulation into a stochastic optimization problem. It is crucial that this approach allows us to determine the number of iteration based on a desired accuracy $\epsilon$, independent of the dataset size $n$. We will show that the proposed stochastic gradient descent algorithm works in general (possible infinite-dimensional) Hilbert spaces, is easy to implement and requires no additional step-size parameters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge