Efficient Dictionary Learning with Sparseness-Enforcing Projections
Paper and Code
Apr 16, 2016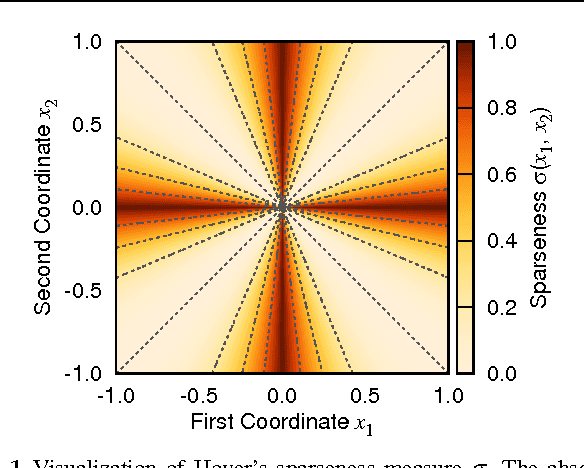
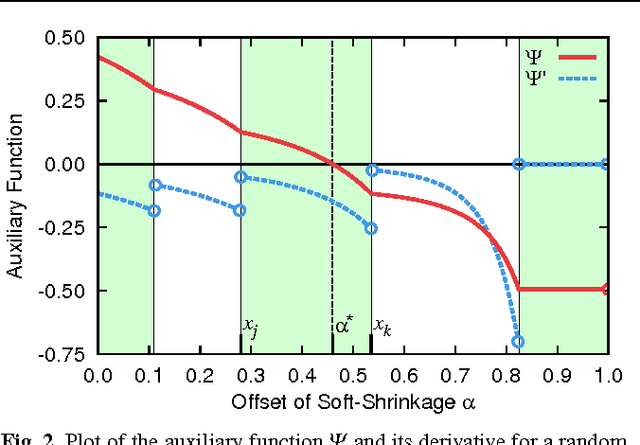
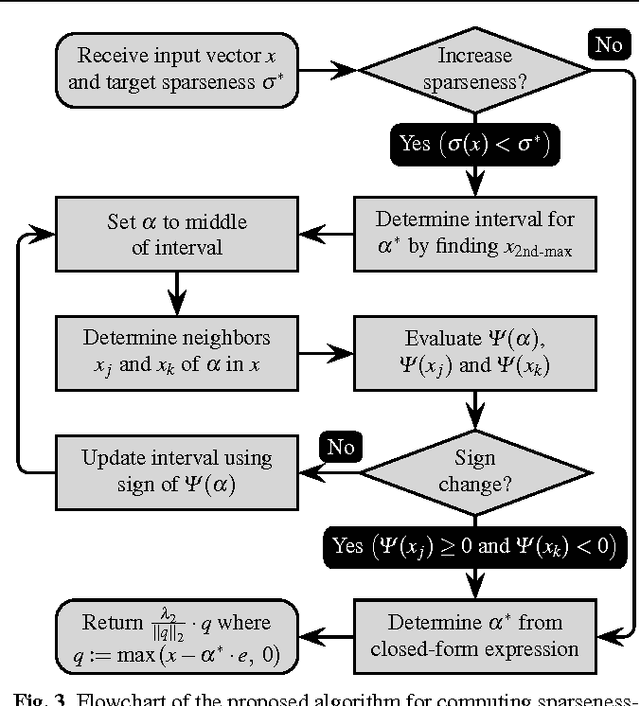
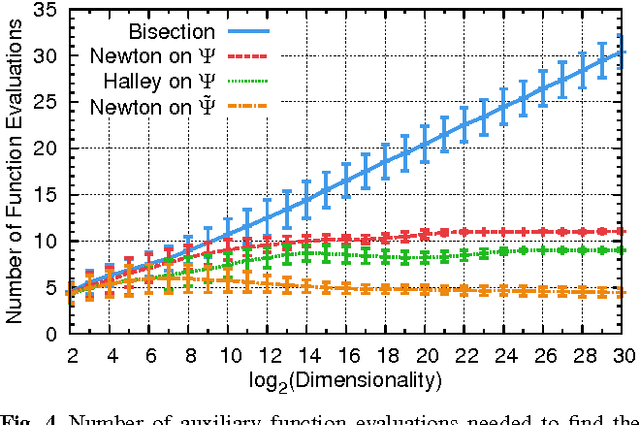
Learning dictionaries suitable for sparse coding instead of using engineered bases has proven effective in a variety of image processing tasks. This paper studies the optimization of dictionaries on image data where the representation is enforced to be explicitly sparse with respect to a smooth, normalized sparseness measure. This involves the computation of Euclidean projections onto level sets of the sparseness measure. While previous algorithms for this optimization problem had at least quasi-linear time complexity, here the first algorithm with linear time complexity and constant space complexity is proposed. The key for this is the mathematically rigorous derivation of a characterization of the projection's result based on a soft-shrinkage function. This theory is applied in an original algorithm called Easy Dictionary Learning (EZDL), which learns dictionaries with a simple and fast-to-compute Hebbian-like learning rule. The new algorithm is efficient, expressive and particularly simple to implement. It is demonstrated that despite its simplicity, the proposed learning algorithm is able to generate a rich variety of dictionaries, in particular a topographic organization of atoms or separable atoms. Further, the dictionaries are as expressive as those of benchmark learning algorithms in terms of the reproduction quality on entire images, and result in an equivalent denoising performance. EZDL learns approximately 30 % faster than the already very efficient Online Dictionary Learning algorithm, and is therefore eligible for rapid data set analysis and problems with vast quantities of learning samples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge