Semi-Oblivious Chase Termination for Linear Existential Rules: An Experimental Study

The chase procedure is a fundamental algorithmic tool in databases that allows us to reason with constraints, such as existential rules, with a plethora of applications. It takes as input a database and a set of constraints, and iteratively completes the database as dictated by the constraints. A key challenge, though, is the fact that it may not terminate, which leads to the problem of checking whether it terminates given a database and a set of constraints. In this work, we focus on the semi-oblivious version of the chase, which is well-suited for practical implementations, and linear existential rules, a central class of constraints with several applications. In this setting, there is a mature body of theoretical work that provides syntactic characterizations of when the chase terminates, algorithms for checking chase termination, precise complexity results, and worst-case optimal bounds on the size of the result of the chase (whenever is finite). Our main objective is to experimentally evaluate the existing chase termination algorithms with the aim of understanding which input parameters affect their performance, clarifying whether they can be used in practice, and revealing their performance limitations.

The Complexity of Why-Provenance for Datalog Queries

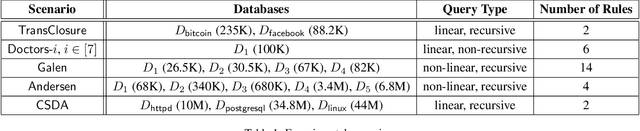
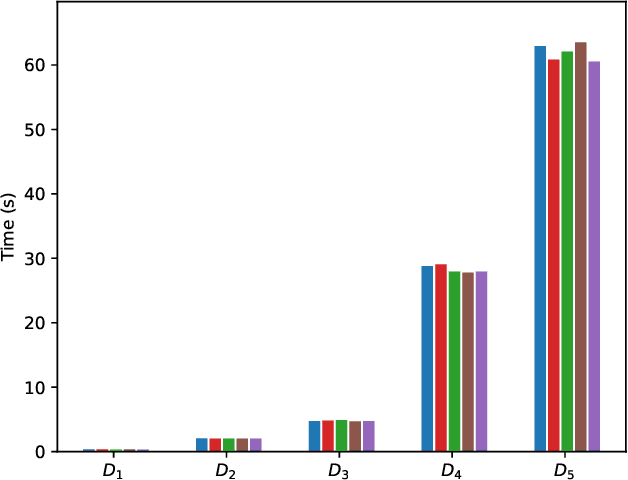
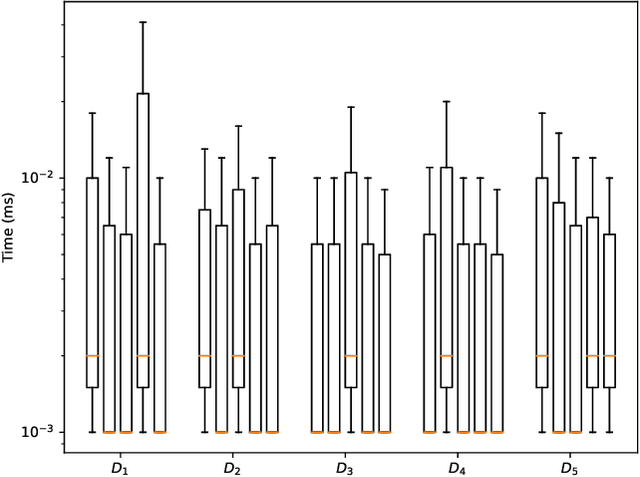
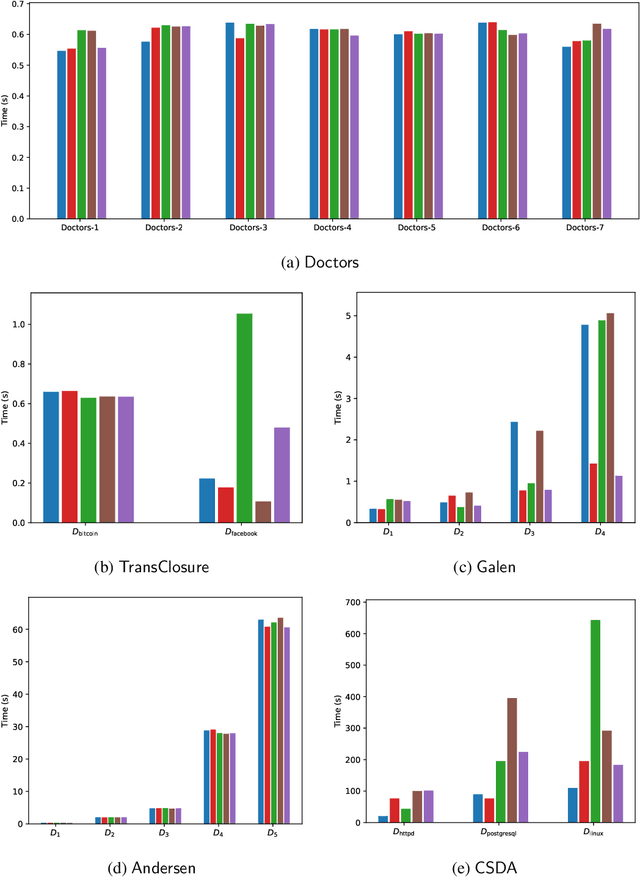
Explaining why a database query result is obtained is an essential task towards the goal of Explainable AI, especially nowadays where expressive database query languages such as Datalog play a critical role in the development of ontology-based applications. A standard way of explaining a query result is the so-called why-provenance, which essentially provides information about the witnesses to a query result in the form of subsets of the input database that are sufficient to derive that result. To our surprise, despite the fact that the notion of why-provenance for Datalog queries has been around for decades and intensively studied, its computational complexity remains unexplored. The goal of this work is to fill this apparent gap in the why-provenance literature. Towards this end, we pinpoint the data complexity of why-provenance for Datalog queries and key subclasses thereof. The takeaway of our work is that why-provenance for recursive queries, even if the recursion is limited to be linear, is an intractable problem, whereas for non-recursive queries is highly tractable. Having said that, we experimentally confirm, by exploiting SAT solvers, that making why-provenance for (recursive) Datalog queries work in practice is not an unrealistic goal.

Absolute Expressiveness of Subgraph Motif Centrality Measures

In graph-based applications, a common task is to pinpoint the most important or ``central'' vertex in a (directed or undirected) graph, or rank the vertices of a graph according to their importance. To this end, a plethora of so-called centrality measures have been proposed in the literature that assess which vertices in a graph are the most important ones. Riveros and Salas, in an ICDT 2020 paper, proposed a family of centrality measures based on the following intuitive principle: the importance of a vertex in a graph is relative to the number of ``relevant'' connected subgraphs, known as subgraph motifs, surrounding it. We refer to the measures derived from the above principle as subgraph motif measures. It has been convincingly argued that subgraph motif measures are well-suited for graph database applications. Although the ICDT paper studied several favourable properties enjoyed by subgraph motif measures, their absolute expressiveness remains largely unexplored. The goal of this work is to precisely characterize the absolute expressiveness of the family of subgraph motif measures.

Non-Uniformly Terminating Chase: Size and Complexity

The chase procedure, originally introduced for checking implication of database constraints, and later on used for computing data exchange solutions, has recently become a central algorithmic tool in rule-based ontological reasoning. In this context, a key problem is non-uniform chase termination: does the chase of a database w.r.t. a rule-based ontology terminate? And if this is the case, what is the size of the result of the chase? We focus on guarded tuple-generating dependencies (TGDs), which form a robust rule-based ontology language, and study the above central questions for the semi-oblivious version of the chase. One of our main findings is that non-uniform semi-oblivious chase termination for guarded TGDs is feasible in polynomial time w.r.t. the database, and the size of the result of the chase (whenever is finite) is linear w.r.t. the database. Towards our results concerning non-uniform chase termination, we show that basic techniques such as simplification and linearization, originally introduced in the context of ontological query answering, can be safely applied to the chase termination problem.

First-Order Rewritability of Frontier-Guarded Ontology-Mediated Queries

We focus on ontology-mediated queries (OMQs) based on (frontier-)guarded existential rules and (unions of) conjunctive queries, and we investigate the problem of FO-rewritability, i.e., whether an OMQ can be rewritten as a first-order query. We adopt two different approaches. The first approach employs standard two-way alternating parity tree automata. Although it does not lead to a tight complexity bound, it provides a transparent solution based on widely known tools. The second approach relies on a sophisticated automata model, known as cost automata. This allows us to show that our problem is 2ExpTime-complete. In both approaches, we provide semantic characterizations of FO-rewritability that are of independent interest.

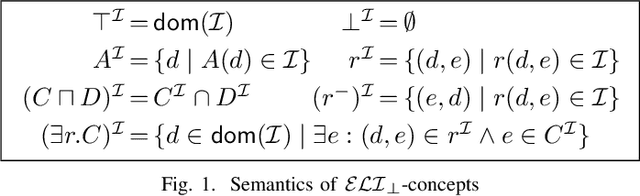
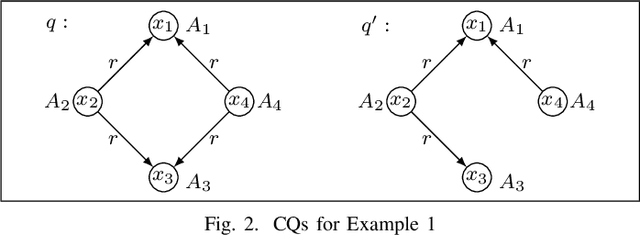
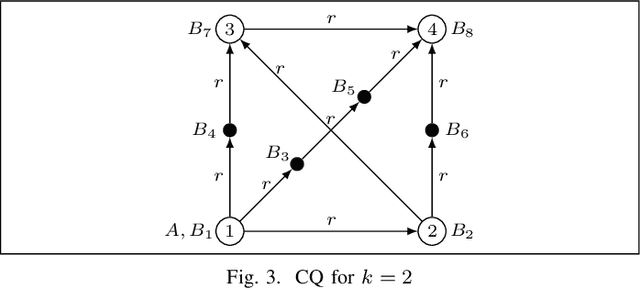
When is Ontology-Mediated Querying Efficient?

In ontology-mediated querying, description logic (DL) ontologies are used to enrich incomplete data with domain knowledge which results in more complete answers to queries. However, the evaluation of ontology-mediated queries (OMQs) over relational databases is computationally hard. This raises the question when OMQ evaluation is efficient, in the sense of being tractable in combined complexity or fixed-parameter tractable. We study this question for a range of ontology-mediated query languages based on several important and widely-used DLs, using unions of conjunctive queries as the actual queries. For the DL ELHI extended with the bottom concept, we provide a characterization of the classes of OMQs that are fixed-parameter tractable. For its fragment EL extended with domain and range restrictions and the bottom concept (which restricts the use of inverse roles), we provide a characterization of the classes of OMQs that are tractable in combined complexity. Both results are in terms of equivalence to OMQs of bounded tree width and rest on a reasonable assumption from parameterized complexity theory. They are similar in spirit to Grohe's seminal characterization of the tractable classes of conjunctive queries over relational databases. We further study the complexity of the meta problem of deciding whether a given OMQ is equivalent to an OMQ of bounded tree width, providing several completeness results that range from NP to 2ExpTime, depending on the DL used. We also consider the DL-Lite family of DLs, including members that admit functional roles.

The Limits of Efficiency for Open- and Closed-World Query Evaluation Under Guarded TGDs

Ontology-mediated querying and querying in the presence of constraints are two key database problems where tuple-generating dependencies (TGDs) play a central role. In ontology-mediated querying, TGDs can formalize the ontology and thus derive additional facts from the given data, while in querying in the presence of constraints, they restrict the set of admissible databases. In this work, we study the limits of efficient query evaluation in the context of the above two problems, focussing on guarded and frontier-guarded TGDs and on UCQs as the actual queries. We show that a class of ontology-mediated queries (OMQs) based on guarded TGDs can be evaluated in FPT iff the OMQs in the class are equivalent to OMQs in which the actual query has bounded treewidth, up to some reasonable assumptions. For querying in the presence of constraints, we consider classes of constraint-query specifications (CQSs) that bundle a set of constraints with an actual query. We show a dichotomy result for CQSs based on guarded TGDs that parallels the one for OMQs except that, additionally, FPT coincides with PTime combined complexity. The proof is based on a novel connection between OMQ and CQS evaluation. Using a direct proof, we also show a similar dichotomy result, again up to some reasonable assumptions, for CQSs based on frontier-guarded TGDs with a bounded number of atoms in TGD heads. Our results on CQSs can be viewed as extensions of Grohe's well-known characterization of the tractable classes of CQs (without constraints). Like Grohe's characterization, all the above results assume that the arity of relation symbols is bounded by a constant. We also study the associated meta problems, i.e., whether a given OMQ or CQS is equivalent to one in which the actual query has bounded treewidth.

The Space-Efficient Core of Vadalog

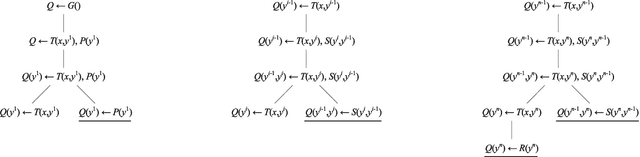
Vadalog is a system for performing complex reasoning tasks such as those required in advanced knowledge graphs. The logical core of the underlying Vadalog language is the warded fragment of tuple-generating dependencies (TGDs). This formalism ensures tractable reasoning in data complexity, while a recent analysis focusing on a practical implementation led to the reasoning algorithm around which the Vadalog system is built. A fundamental question that has emerged in the context of Vadalog is the following: can we limit the recursion allowed by wardedness in order to obtain a formalism that provides a convenient syntax for expressing useful recursive statements, and at the same time achieves space-efficiency? After analyzing several real-life examples of warded sets of TGDs provided by our industrial partners, as well as recent benchmarks, we observed that recursion is often used in a restricted way: the body of a TGD contains at most one atom whose predicate is mutually recursive with a predicate in the head. We show that this type of recursion, known as piece-wise linear in the Datalog literature, is the answer to our main question. We further show that piece-wise linear recursion alone, without the wardedness condition, is not enough as it leads to the undecidability of reasoning. We finally study the relative expressiveness of the query languages based on (piece-wise linear) warded sets of TGDs.

Containment for Rule-Based Ontology-Mediated Queries

Many efforts have been dedicated to identifying restrictions on ontologies expressed as tuple-generating dependencies (tgds), a.k.a. existential rules, that lead to the decidability for the problem of answering ontology-mediated queries (OMQs). This has given rise to three families of formalisms: guarded, non-recursive, and sticky sets of tgds. In this work, we study the containment problem for OMQs expressed in such formalisms, which is a key ingredient for solving static analysis tasks associated with them. Our main contribution is the development of specially tailored techniques for OMQ containment under the classes of tgds stated above. This enables us to obtain sharp complexity bounds for the problems at hand, which in turn allow us to delimitate its practical applicability. We also apply our techniques to pinpoint the complexity of problems associated with two emerging applications of OMQ containment: distribution over components and UCQ rewritability of OMQs.